Good judgment comes from experience, and experience – well, that comes from poor judgment.

― A.A. Milne

To avoid the sort of implicit assumption of ZERO uncertainty one can use (expert) judgment to fill in the information gap. This can be accomplished in a distinctly principled fashion and always works better with a basis in evidence. The key is the recognition that we base our uncertainty on a model (a model that is associated with error too). The models are fairly standard and need a certain minimum amount of information to be solvable, and we are always better off with too much information making it effectively over-determined. Here we look at several forms of models that lead to uncertainty estimation including discretization error, and statistical models applicable to epistemic or experimental uncertainty.

Maturity, one discovers, has everything to do with the acceptance of ‘not knowing.

― Mark Z. Danielewski

For discretization error the model is quite simple where is the mesh converged solution, is the solution on the mesh and is the mesh length scale, is the (observed) rate of convergence, and is a proportionality constant. We have three unknowns so we need at leastmeshes to solve the error model exactly or more if we solve it in some sort of optimal manner. We recently had a method published that discusses how to include expert judgment in the determination of numerical error and uncertainty using models of this type. This model can be solved along with data using minimization techniques including the expert judgment as constraints on the solution for the unknowns. For both the over- or the under-determined cases different minimizations one can get multiple solutions to the model and robust statistical techniques may be used to find the “best” answers. This means that one needs to resort to more than simple curve fitting, and least squares procedures; one needs to solve a nonlinear problem associated with minimizing the fitting error (i.e., residuals) with respect to other error representations.

For extreme under-determined cases unknown variables can be completely eliminated by simply choosing the solution based on expert judgment. For numerical error an obvious example is assuming that calculations are converging at an expert-defined rate. Of course the rate assumed needs an adequate justification based on a combination of information associated with the nature of the numerical method and the solution to the problem. A key assumption that often does not hold up is the achievement of the method’s theoretical rate of convergence for realistic problems. In many cases a high-order method will perform at a lower rate of convergence because the problem has a structure with less regularity than necessary for the high-order accuracy. Problems with shocks or other forms of discontinuities will not usually support high-order results and a good operating assumption is a first-order convergence rate.

To make things concrete let’s tackle a couple of examples of how all of this might work. In the paper published recently we looked at solution verification when people use two meshes instead of the three needed to fully determine the error model. This seems kind of extreme, but in this post the example is the cases where people only use a single mesh. Seemingly we can do nothing at all to estimate uncertainty, but as I explained last week, this is the time to bear down and include an uncertainty because it is the most uncertain situation, and the most important time to assess it. Instead people throw up their hands and do nothing at all, which is the worst thing to do. So we have a single solution at and need to add information to allow the solution of our error model, . The simplest way to get to an solvable error model is to simply propose a value for the mesh converged solution, , which then can be used to provide an uncertainty estimate,    |A – multiplied by an appropriate safety factor .

This is a rather strong assumption to make. We might be better served by providing a range values for either the convergence rate of the solution itself. In this way we provide a bit more deference in what we are suggesting as the level of uncertainty, which is definitely called for in this case since we are so information poor. Again the use of an appropriate safety factor is called for, on the order of 2 to 3 in value. From statistical arguments the safety factor of 2 has some merit while 3 is associated with solution verification practice proposed by Roache. All of this is strongly associated with the need to make an estimate in a case where too little work has been done to make a direct estimate. If we are adding information that is weakly related to the actual problem we are solving, the safety factor is essential to account for the lack of knowledge. Furthermore we want to enable the circumstance where more work in active problem solving will allow the uncertainties to be reduced!

A lot of this information is probably good to include as part of the analysis when you have enough information too. The right way to think about this information is as constraints on the solution. If the constraints are active they have been triggered by the analysis and help determine the solution. If the constraints have no effect on the solution then they are proven to be correct given the data. In this way the solution can be shown to be consistent with the views of the expertise. If one is in the circumstance where the expert judgment is completely determining the solution, one should be very wary as this is a big red flag.

Other numerical effects need models for their error and uncertainty too. Linear and nonlinear error plus round-off error all can contribute to the overall uncertainty. A starting point would be the same model as the discretization error, but using the tolerances from the linear or nonlinear solution as . The starting assumption is often that these are dominated by discretization error, or tied to the discretization. Evidence in support of these assumptions is generally weak to nonexistent. For round-off errors the modeling is similar, but all of these errors can be magnified in the face of instability. A key is to provide some sort of assessment of their aggregate impact on the results and not explicitly ignore them.

Other parts of the uncertainty estimation are much more amenable to statistical structures for uncertainty. This includes the type of uncertainty that too often provides (wrongly!) the entirety of uncertainty estimation, parametric uncertainty. This problem is a direct result of the availability of tools that allow the estimation of parametric uncertainty magnitude. In addition to parametric uncertainty, random aleatory uncertainties, experimental uncertainty and deep model form uncertainty all may be examined using statistical approaches. In many ways the situation is far better than for discretization error, but in other ways the situation more dire. Things are better because statistical models can be evaluated using less data, and errors can be estimated using standard approaches. The situation is dire because often the issues being radically under-sampled are reality, not the model of reality simulations are based on.

Uncertainty is a quality to be cherished, therefore – if not for it, who would dare to undertake anything?

― Villiers de L’Isle-Adam

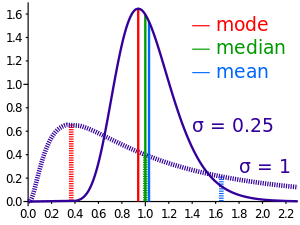
In the same way as numerical uncertainty, the first thing to decide upon is the model. A standard modeling assumption is the use of the normal or Gaussian distribution as the starting assumption. This is almost always chosen as a default. A reasonable blog post title would be “The default probability distribution is always Gaussian”. A good thing for a distribution is that we can start to assess it beginning with two data points. A bad and common situation is that we only have a single data point. Thus uncertainty estimation is impossible without adding information from somewhere, and an expert judgment is the obvious place to look. With statistical data and its quality we can apply the standard error estimation using the sample size to scale the additional uncertainty driven by poor sampling, where is the number of samples.

There are some simple ideas to apply in the case of the assumed Gaussian and a single data point. A couple of reasonable pieces of information can be added, one being an expert judged standard deviation and then by fiat making the single data point the mean of the distribution. A second assumption could be used where the mean of the distribution is defined by expert judgment, which then defines the standard deviation,  |A – where is the defined mean, and is the data point. In these cases the standard error estimate would be equal to where . Both of these approaches have the strengths and weaknesses, and include the strong assumption of the normal distribution.

In a lot of cases a better simple assumption about the statistical distribution would be to use a uniform distribution. The issue with the uniform distribution would be identifying the width of the distribution. To define the basic distribution you need at least two pieces of information just as the normal (Gaussian) distribution. The subtleties are different and need some discussion. The width of a uniform distribution is defined by – . A question is how representative a single piece of information would actually be? Does one center the distribution about ? One could be left with needing to add two pieces of information instead of one by defining and . This then allows a fairly straightforward assessment of the uncertainty.

For statistical models eventually one might resort to using a Bayesian method to encode the expert judgment in defining a prior distribution. In general terms this might seem to be an absolutely key approach to structure the expert judgment where statistical modeling is called for. The basic form of Bayes theorem is where is the probability of given , is the probability of and so on. A great deal of the power of the method depends on having a good (or expert) handle on all the terms on the right hand side of the equation. Bayes theorem would seem to be an ideal framework for the application of expert judgment through the decision about the nature of the prior.

The mistake is thinking that there can be an antidote to the uncertainty.

― David Levithan

A key to this entire discussion is the need to resist the default uncertainty of ZERO as a principle. It would be best if real problem specific work were conducted to estimate uncertainties, the right calculations, right meshes and right experiments. If one doesn’t have the time, money or willingness, the answer is to call upon experts to fill in the gap using justifiable assumptions and information while taking an appropriate penalty for the lack of effort. This would go a long way to improving the state of practice in computational science, modeling and simulation.

Children must be taught how to think, not what to think.

― Margaret Mead

Rider, William, Walt Witkowski, James R. Kamm, and Tim Wildey. “Robust verification analysis.” Journal of Computational Physics 307 (2016): 146-163.

 

As long as you’re moving, it’s easier to steer.

― Anonymous

Just to be clear, this isn’t a good thing; it is a very bad thing!

I have noticed that we tend to accept a phenomenally common and undeniably unfortunate practice where a failure to assess uncertainty means that the uncertainty reported (acknowledged, accepted) is identically ZERO. In other words if we do nothing at all, no work, no judgment, the work (modeling, simulation, experiment, test) is allowed to provide an uncertainty that is ZERO. This encourages scientists and engineers to continue to do nothing because this wildly optimistic assessment is a seeming benefit. If somebody does work to estimate the uncertainty the degree of uncertainty always gets larger as a result. This practice is desperately harmful to the practice and progress in science and incredibly common.

Of course this isn’t the reality, the uncertainty is actually some value, but the lack of assessed uncertainty is allowed to be accepted as ZERO. The problem is the failure of other scientists and engineers to demand an assessment instead of simply accepting the lack of due diligence or outright curiosity and common sense. The reality is that the situation where the lack of knowledge is so dramatic, the estimated uncertainty should actually be much larger to account for this lack of knowledge. Instead we create a cynical cycle where more information is greeted by more uncertainty rather than less. The only way to create a virtuous cycle is the acknowledgement that little information should mean large uncertainties, and part of the reward for good work is greater certainty (and lower uncertainty).

This entire post is related to a rather simple observation that has broad applications for how science and engineering is practiced today. A great deal of work has this zero uncertainty writ large, i.e., there is no reported uncertainty at all, none, ZERO. Yet, despite of the demonstrable and manifest shortcomings, a gullible or lazy community readily accepts the incomplete work. Some of the better work has uncertainties associated with it, but almost always varying degrees of incompleteness. Of course one should acknowledge up front that uncertainty estimation is always incomplete, but the degree of incompleteness can be spellbindingly large.

One way to deal with all of this uncertainty is to introduce a taxonomy of uncertainty where we can start to organize our lack of knowledge. For modeling and simulation exercises I’m suggesting that three big bins for uncertainty be used: numerical, epistemic modeling, and modeling discrepancy. Each of these categories has additional subcategories that may be used to organize the work toward a better and more complete technical assessment. In the definition for each category we get the idea of the texture in each, and an explicit view of intrinsic incompleteness.

• Numerical: Discretization (time, space, distribution), nonlinear approximation, linear convergence, mesh, geometry, parallel computation, roundoff,…
• Epistemic Modeling: black box parametric, Bayesian, white box testing, evidence theory, polynomial chaos, boundary conditions, initial conditions, statistical,…
• Modeling discrepancy: Data uncertainty, model form, mean uncertainty, systematic bias, boundary conditions, initial conditions, measurement, statistical, …

A very specific thing to note is that the ability to assess any of these uncertainties is always incomplete and inadequate. Admitting and providing some deference to this nature is extremely important in getting to a better state of affairs. A general principle to strive for in uncertainty estimation is a state where the application of greater effort yields smaller uncertainties. A way to achieve this nature of things is to penalize the uncertainty estimation to account for incomplete information. Statistical methods always account for sampling by increasing a standard error proportionally to the root of the number of samples. As such there is an explicit benefit for gathering more data to reduce the uncertainty. This sort of measure is well suited to encourage a virtuous cycle of information collection. Instead modeling and simulation accepts a poisonous cycle where more information implicitly penalizes the effort by increasing uncertainty.

This whole post is predicated on the observation that we willingly enter into a system where effort increases the uncertainty. The direct opposite should be the objective where more effort results in smaller uncertainty. We also need to embrace a state where we recognize that the universe has an irreducible core of uncertainty. Admitting that perfect knowledge and prediction is impossible will allow us to focus more acutely on what we can predict. This is really a situation where we are willfully ignorant and over-confident about your knowledge. One might tag some of the general issue with reproducibility and replicatability of science to the same phenomena. Any effort that reports to provide a perfect set of data perfectly predicting reality should be rejected as being utterly ridiculous.

One of the next things to bring to the table is the application of expert knowledge and judgment to fill in where stronger technical work is missing. Today expert judgment is implicitly present in the lack of assessment. It is a dangerous situation where experts simply assert that things are true or certain. Instead of this expert system being directly identified, it is embedded in the results. A much better state of affairs is to ask for the uncertainty and the evidence for its value. If there has been work to assess the uncertainty this can be provided. If instead, the uncertainty is based on some sort expert judgment or previous experience, the evidence can be provided in this form.

Now let us be more concrete in the example of what this sort of evidence might look like within the expressed taxonomy for uncertainty. I’ll start with numerical uncertainty estimation that is the most commonly completely non-assessed uncertainty. Far too often a single calculation is simply shown and used without any discussion. In slightly better cases, the calculation will be given with some comments on the sensitivity of the results to the mesh and the statement that numerical errors are negligible at the mesh given. Don’t buy it! This is usually complete bullshit! In every case where no quantitative uncertainty is explicitly provided, you should be suspicious. In other cases unless the reasoning is stated as being expertise or experience it should be questioned. If it is stated as being experiential then the basis for this experience and its documentation should be given explicitly along with evidence that it is directly relevant.

So what does a better assessment look like?

Under ideal circumstances you would use a model for the error (uncertainty) and do enough computational work to determine the model. The model or models would characterize all of the numerical effects influencing results. Most commonly, the discretization error is assumed to be the dominant numerical uncertainty (again evidence should be given). If the error can be defined as being dependent on a single spatial length scale, the standard error model can be used and requires three meshes be used to determine its coefficients. This best practice is remarkably uncommon in practice. If fewer meshes are used, the model is under-determined and information in terms of expert judgment should be added. I have worked on the case of only two meshes being used, but it is clear what to do in that case.

In many cases there is no second mesh to provide any basis for standard numerical error estimation. Far too many calculational efforts provide a single calculation without any idea of the requisite uncertainties. In a nutshell, the philosophy in many cases is that the goal is to complete the best single calculation possible and creating a calculation that is capable of being assessed is not a priority. In other words the value proposition for computation is either do the best single calculation without any idea of the uncertainty versus a lower quality simulation with a well-defined assessment of uncertainty. Today the best single calculation is the default approach. This best single calculation then uses the default uncertainty estimate of exactly ZERO because nothing else is done. We need to adopt an attitude that will reject this approach because of the dangers associated with accepting a calculation without any quality assessment.

In the absence of data and direct work to support a strong technical assessment of uncertainty we have no choice except to provide evidence via expert judgment and experience. A significant advance would be a general sense that such assessments be expected and the default ZERO uncertainty is never accepted. For example there are situations where single experiments are conducted without any knowledge of how the results of the experiment fit within any distribution of results. The standard approach to modeling is a desire to exactly replicate the results as if the experiment were a well-posed initial value problem instead of one realization of a distribution of results. We end up chasing our tails in the process and inhibiting progress. Again we are left in the same boat, as before, the default uncertainty in the experimental data is ZERO. Instead we have no serious attempt to examine the width and nature of the distribution in our assessments. The result is a lack of focus on the true nature of our problems and inhibitions on progress.

The problems just continue in the assessment of various uncertainty sources. In many cases the practice of uncertainty estimation is viewed only as the establishment of the degree of uncertainty is modeling parameters used in various closure models. This is often termed as epistemic uncertainty or lack of knowledge. This sometimes provides the only identified uncertainty in a calculation because tools exist for creating this data from calculations (often using a Monte Carlo sampling approach). In other words the parametric uncertainty is often presented as being all the uncertainty! Such studies are rarely complete and always fail to include the full spectrum of parameters in modeling. Such studies are intrinsically limited by being embedded in a code that has other unchallenged assumptions.

This is a virtue, but ignores broader modeling issues almost completely. For example the basic equations and model used in simulations is rarely, if ever questioned. The governing equations minus the closure are assumed to be correct a priori. This is an extremely dangerous situation because these equations are not handed down from the creator on stone tablets, but full of assumptions that should be challenged and validated with regularity. Instead this happens with such complete rarity despite being the dominant source of error in cases. When this is true the capacity to create a predictive simulation is completely impossible. Take the application of incompressible flow equations, which is rarely questioned. These equations have a number of stark approximations that are taken as the truth almost without thought. The various unphysical aspects of the approximation are ignored. For compressible flow the equations are based on equilibrium assumptions, which are rarely challenged or studied.

A second area of systematic and egregious oversight by the community is aleatory or random uncertainty. This sort of uncertainty is clearly overlooked by our modeling approach in a way that most people fail to appreciate. Our models and governing equations are oriented toward solving the average or mean solution for a given engineering or science problem. This key question is usually muddled together in modeling by adopting an approach that mixes a specific experimental event with a model focused on the average. This results in a model that has an unclear separation of the general and specific. Few experiments or events being simulated are viewed from the context that they are simply a single instantiation of a distribution of possible outcomes. The distribution of possible outcomes is generally completely unknown and not even considered. This leads to an important source of systematic uncertainty that is completely ignored.

It doesn’t matter how beautiful your theory is … If it doesn’t agree with experiment, it’s wrong.

― Richard Feynman

Almost every validation exercise tries to examine the experiment as a well-posed initial value problem with a single correct answer instead of a single possible realization from an unknown distribution. More and more the nature of the distribution is the core of the scientific or engineering question we want to answer, yet our modeling approach is hopelessly stuck in the past because we are not framing the question we are answering thoughtfully. Often the key question we need to answer is how likely a certain bad outcome will be. We want to know the likelihood of extreme events given a set of changes in a system. Think about things like what does a hundred year flood look like under a scenario of climate change, or the likelihood that a mechanical part might fail under normal usage. Instead our fundamental models being the average response for the system are left to infer these extreme events from the average often without any knowledge of the underlying distributions. This implies a need to change the fundamental approach we take to modeling, but we won’t until we start to ask the right questions and characterize the right uncertainties.

One should avoid carrying out an experiment requiring more than 10 per cent accuracy.

― Walther Nernst

The key to progress is work toward some best practices that avoid these pitfalls. First and foremost a modeling and simulation activity should never allow itself to report or even imply that key uncertainties be ZERO. If one has lots of data and make efforts to assess then uncertainties can be assigned through strong technical arguments. This is terribly or even embarrassingly uncommon even today. If one does not have the data or calculations to support uncertainty estimation then significant amounts of expert judgment and strong assumptions are necessary to estimate uncertainties. The key is to make a significant commitment to being honest about what isn’t known and take a penalty for lack of knowledge and understanding. That penalty should be well grounded in evidence and experience. Making progress in these areas is essential to make modeling and simulation a vehicle appropriate to the hype we hear all the time.

Stagnation is self-abdication.

― Ryan Talbot

Modeling and simulation is looked at as one of the great opportunities for industrial, scientific and engineering improvements for society. Right now we are hinging our improvements on a mass of software being moved onto increasingly exotic (and powerful) computers. Increasingly the whole of our effort in modeling and simulation is being reduced to nothing but a software development activity. The holistic and integrating nature of modeling and simulation is being hollowed out and lost to a series of fatal assumptions. One of the places where computing’s power cannot change is how we practice our computational efforts. It can enable the practices in modeling and simulation by making it possible to do more computation. The key to fixing this dynamic is a commitment to understanding the nature and limits of our capability. Today we just assume that our modeling and simulation has mastery and no such assessment is needed.

The computational capability does nothing to improve experimental sciences necessary value in challenging our theory. Moreover the whole sequence of necessary activities like model development, and analysis, method and algorithm development along with experimental science and engineering are all receiving almost no attention today. These activities are absolutely necessary for modeling and simulation success along with the sort of systematic practices I’ve elaborated on in this post. Without a sea change in the attitude toward how modeling and simulation is practiced and what it depends upon, its promise as a technology will be stillborn and nullified by our collective hubris.

It is high time for those working to progress modeling and simulation to focus energy and effort it is needed. Today we are avoiding a rational discussion of how to make modeling and simulation successful, and relying on hype to govern our decisions. The goal should not be to assure that high performance computing is healthy, but rather modeling and simulation (or big data analysis) is healthy. High performance computing is simply a necessary tool for these capabilities, but not the soul of either. We need to make sure the soul of modeling and simulation is healthy rather than the corrupted mass of stagnation we have.

You view the world from within a model.

― Nassim Nicholas Taleb

 

…beauty is not symmetry of parts- that’s so impotent -as Mishima says, beauty is something that attacks, overpowers, robs, & finally destroys…

― John Geddes

In much of physics a great deal is made of the power of symmetry. The belief is that symmetry is a powerful tool, but also a compelling source of beauty and depth. In fluid mechanics the really cool stuff happens when the symmetry is broken. The power and depth of consequence comes from the asymmetric part of the solution. When things are symmetric they tend to be boring and uninteresting, and nothing beautiful or complex arises. I’ll be so bold as to say that the power of this essential asymmetry hasn’t been fully exploited, but could be even more magnificent.

Fluid mechanics at its simplest is something called Stokes flow, basically motion so slow that it is solely governed by viscous forces. This is the asymptotic state where the Reynolds number (the ratio of inertial to viscous forces) is identically zero. It’s a bit oxymoronic as it is never reached, it’s the equations of motion without any motion or where the motion can be ignored. In this limit flows preserve their basic symmetries to a very high degree.

Basically nothing interesting happens and the whole thing is basically a giant boring glop of nothing. It is nice because lots of pretty math can be done in this limit. The equations are very well behaved and solutions have tremendous regularity and simplicity. Let the fluid move and take the Reynolds number away from zero and cool things almost immediately happen. The big thing is the symmetry is broken and the flow begins to contort, and wind into amazing shapes. Continue to raise the Reynolds number and the asymmetries pile up and we have turbulence, chaos and our understanding goes out the window. At the same time the whole thing produces patterns and structures of immense and inspiring beauty. With symmetry fluid mechanics is dull as dirt; without symmetry it is amazing and something to marveled at.

So, let’s dig a bit deeper into the nature of these asymmetries and the opportunity to take them even further.

The fundamental asymmetry in physics is the arrow of time, and its close association with entropy. The connection with asymmetry and entropy is quite clear and strong for shock waves where the mathematical theory is well-developed and accepted. The simplest case to examine is Burgers’ equation, , or its conservation form . This equation supports shocks and rarefactions, and their formation is determined by the sign of . If one takes the gradient of the governing equation in space, you can see the solution forms a Ricatti equation along characteristics, . The solution on characteristics tells one the fate of the solution, . The thing to recognize that the denominator will go to zero if and the value of the derivative will become unbounded, i.e., form a shock.

The process in fluid dynamics is similar. If the viscosity is sufficiently small and the gradients of velocity are negative, a shock will form. It is inevitable as death and taxes. Moving back to Burgers’ equation briefly we can also see another aspect of the dynamics that isn’t so commonly known, the presence of dissipation in the absence of viscosity. Without viscosity for the rarefied flow where gradients diminish there is no dissipation. For a shock there is dissipation, and the form of it will be quite familiar by the end of the post. If one forms an equation for the evolution of the energy in a Burgers’ flow and looks at the solution for a shock via the jump conditions a discrepancy is uncovered, the rate of kinetic energy dissipation is . The same basic character is shared by shock waves and incompressible turbulent flows. It implies the presence of a discontinuity in the model of the flow.

On the one hand the form seems to be unavoidable dimensionally, on the other it is a profound result that provides the basis of the Clay prize for turbulence. It gets to the core of my belief that to a very large degree the understanding of turbulence will elude us as long as we use the intrinsically unphysical incompressible approximation. This may seem controversial, but incompressibility is an approximation to reality, not a fundamental relation. As such its utility is dependent upon the application. It is undeniably useful, but has limits, which are shamelessly exposed by turbulence. Without viscosity the equations governing incompressible flows are pathological in the extreme. Deep mathematical analysis has been unable to find singular solutions of the nature needed to explain turbulence in incompressible flows.

The real key to understanding the issues goes to a fundamental misunderstanding about shock waves and compressibility. First, it would be very good to elaborate how the same dynamic manifests itself for the compressible Euler equations. For intents and purposes the way to look at shock formation in the Euler equations acts just like Burgers’ equation for the nonlinear characteristics. In its simplest form the Euler equations have three fundamental characteristic modes, two being nonlinear associated with acoustic (sound) waves, one being linear and associated with material motion. The nonlinear acoustic modes act just like Burgers’ equation, and propagate at a velocity of where is the fluid velocity, and is the speed of sound.

Once the Euler equations are decomposed into the characteristics and the flow is smooth everything follows as Burgers’ equation. Along the appropriate characteristic, the flow will be modulated according to the nonlinearity of the equations, which is slightly different than Burgers’ in an important manner. The nonlinearity now depends on the equation of state in a key was, the curvature of an isentrope, . This quantity is dominantly and asymptotically positive (i.e., convex), but may be negative. For ideal gases . For convex equations of state shocks then always form given enough time if the velocity gradient is negative just like Burgers’ equation.

One key thing to recognize is that the formation of the shock does not depend on the underlying Mach number of the flow. A shock always forms if the velocity is negative even as the Mach number goes to zero (the incompressible limit). Almost everything else follows as with Burgers’ equation including the dissipation relation associated with a shock wave, . Once the shock forms, the dissipation rate is proportional to the cube of the jump across the shock. In addition this limit is actually most appropriate in the zero Mach number limit (i.e., the same limit as incompressible flow!).

Shocks aren’t just supersonic phenomena; they are a result of solving the equations in a limit where this viscous terms are small enough to neglect (i.e., the high Reynolds’ number limit!). So just to sum up, the shock formation along with intrinsic dissipation is most valid in the limits where we think of turbulence. We see that this key effect is a direct result of the asymmetric effect of a velocity gradient on the flow. For most flows where the equation of state is convex, the negative velocity gradient sharpens flow features into shocks that dissipate energy regardless of the value of viscosity. Positive velocity gradients smooth the flow and modify the flow via rarefying the flow. Note that physically admissible non-convex equations of state (really isolated regions in state space) have the opposite character. If one could run a classical turbulence experiment where the fluid is non-convex, the conceptual leap I am suggesting could be tested directly because the asymmetry in turbulence would be associated with positive rather than negative velocity gradients.

Now we can examine the basic known theory of turbulence that is so vexing to everyone. Kolmogorov came up with three key relations for turbulent flows. The spectral nature of turbulence is the best known where one looks at the frequency decomposition of the turbulence flow, and finds a distinct region where the decay of energy shows -5/3 slope. There is a lesser know relation of velocity correlations known as the 2/3 law. I believe the most important relation is known as the 4/5 law for the asymptotic decay of kinetic energy in a high Reynolds number turbulent flow. This equation implies that dissipation occurs in the absence of viscosity (sound familiar?).

The law is stated as . The subscript means longitudinal where the differences are taken in the direction the velocity is moving over a distance . This relation implies a distinct asymmetry in the equations that means negative gradients are intrinsically sharper than positive gradients. This is exactly what happens in compressible flows. Kolmogorov derived this relation from the incompressible flow equations and it has been strongly confirmed by observations. The whole issue associated with the (in)famous Clay prize is the explanation of this law in the mathematical admissible solutions of the incompressible equations. This law suggests that the incompressible flow equations must support singularities that are in essence like a shock. My point is that the compressible equations support exactly the phenomena we seek in the right limits for turbulence. The compressible equations have none of the pathologies of the incompressible equations and have a far greater physical basis and remove the unphysical aspects of the physical-mathematical description.

The result is a conclusion that the incompressible equations are inappropriate for understanding what is happening fundamentally in turbulence. The right way to think about it is that turbulent relations are supported by the basic physics of compressible flows in the right asymptotic limits of zero Mach number, high Reynolds number limits.

Symmetry is what we see at a glance; based on the fact that there is no reason for any difference…

― Blaise Pascal

It isn’t all over; everything has not been invented; the human adventure is just beginning.

― Gene Roddenberry

Listening to the dialog on modeling and simulation is so depressing. There seems to be an assumption implicit to every discussion that all we need to do to unleash predictivesimulation is build the next generation of computers. The proposition is so shallow on the face of it as to be utterly laughable. Except no one is laughing, the programs are predicated on it. The whole mentality is damaging because it intrinsically limits our thinking about how to balance the various elements needed for progress. We see a lack of the sort of approach that can lead to progress with experimental work starved of funding and focus without the needed mathematical modeling effort necessary for utility. Actual applied mathematics has become a veritable endangered species only seen rarely in the wild.

Often a sign of expertise is noticing what doesn’t happen.

― Malcolm Gladwell

One of the really annoying aspects of the hype around computing these days is the lack of practical and pragmatic perspective on what might constitute progress. Among the topics revolving around modeling and simulation practice is the pervasive need for singularities of various types in realistic calculations of practical significance. Much of the dialog and dynamic technically seems to completely avoid the issue and act as if it isn’t a driving concern. The reality is that singularities of various forms and functions are an ever-present aspect of realistic problems and their mediation is an absolutely essential for modeling and simulation’s impact to be fully felt. We still have serious issues because of our somewhat delusional dialog on singularities.

At a fundamental level we can state that singularities don’t exist in nature, but very small or thin structures do whose details don’t matter for large scale phenomena. Thus singularities are a mathematical feature of models for large scale behavior that ignore small scale details. As such when we talk about the behavior of singularities, we are really just looking at models, and asking whether the model’s behavior is good. The important aspect of the things we call singularities is their impact on the large scale and the capacity to do useful things without looking at the small-scale details. Much, if not all of the current drive for computational power is focused on brute force submission of the small-scale details. This approach fails to ignite the sort of deep understanding that a model, which ignoring the small scales requires. Such understanding is the real role of science, not simply overwhelming things with technology.

The role of genius is not to complicate the simple, but to simplify the complicated.

― Criss Jami

The important this to capture is the universality of the small scale’s impact on the large scale. It is closely and intimately related to ideas around the role of stochastic, random structures and models for average behavior. One of the key things to really straighten out is the nature of the question we are asking the model to answer. If the question isn’t clearly articulated, the model will provide deceptive answers that will send scientists and engineers in the wrong direction. Getting this model to question dynamic sorted out is far more important to the success of modeling and simulation than any advance in computing power. It is also completely and utterly off the radar of the modern research agenda. I worry that the present focus will produce damage to the forces of progress that may take decades to undue.

A key place where singularities regularly show up is representations of geometry. It is really useful to represent things with sharp corners and rapid transitions geometrically. Our ability to simulate anything engineered would suffer immensely is we had to compute the detailed smooth parts of geometry. In many cases the detail is then computed with a sort of subgrid model, like surface roughness to represent the impact of the true non-idealized geometry. This is a key example of the treatment of such details as being almost entirely physic’s domain specific. There is not a systematic view of this across fields. The same sort of effect shows up when we marry parts together with the same or different materials.

An expert is someone who knows some of the worst mistakes that can be made in his subject, and how to avoid them.

― Werner Heisenberg

Again the details are immense, the simplification is an absolute necessity. The question that looms over all these discussion is the availability of a mathematical theory that allows the small scale to be ignored, which explains physical phenomena. This would imply a structure for the regularized singularity, and a recipe for successful simulation. For geometric singularities any theory is completely ad hoc and largely missing. Any such theory needs detailed and focused experimental confirmation and attention. As things work today, the basic structure is missing and is relegated to being applied in a domain science manner. We find that this is strong in fluid dynamics, and perhaps plasma physics, but almost absent in many other fields like solid mechanics, the utility of modeling and simulation suffers mightily from this.

If there is any place where singularities are dealt with systematically and properly it is fluid mechanics. Even in fluid mechanics there is a frighteningly large amount of missing territory most acutely in turbulence. The place where things really work is shock waves and we have some very bright people to thank for the order. We can calculate an immense amount of physical phenomena where shock waves are important while ignoring a tremendous amount of detail. All that matter is for the calculation to provide the appropriate integral content of dissipation from the shock wave, and the calculation is wonderfully stable and physical. It is almost never necessary and almost certainly wasteful to compute the full gory details of a shock wave.

Fluid mechanics has many nuances and details with important applications. The mathematical structure of fluids is remarkably well in hand. Boundary layer theory is another monument where our understanding is well defined. It isn’t quite as profoundly satisfying as shocks, but we can do a lot of wonderful things. Many important technological items are well defined and engineered with the able assistance of boundary layer theory. We have a great deal of faith in this knowledge and the understanding of what will happen. The state is better than it is problematic. As boundary layers get more and more exciting they lead to a place where problems abound, the problems that appear when a flow becomes turbulent. All of a sudden the structure becomes much more difficult and prediction with deep understanding starts to elude us.

The same can’t be said by and large for turbulence. We don’t understand it very well at all. We have a lot of empirical modeling and convention wisdom that allows useful science and engineering to proceed, but an understanding like we have for shock waves eludes us. It is so elusive that we have a prize (the Clay prize) focused on providing a deep understanding of the mathematical physics of its dynamics. The problem is that the physics strongly implies that the behavior of the governing equations (incompressible Navier-Stokes) admits a singularity, yet the equations don’t seem to. Such a fundamental incongruence is limiting our ability to progress. I believe the issue is the nature of the governing equations and a need to change this model away from incompressibility, which is a useful and unphysical approximation, not a fundamental physical law. In spite of all the problems, the state of affairs in turbulence is remarkably good compared with solid mechanics.

Another discontinuous behavior of great importance in practical matters are material interfaces. Again these interfaces are never truly singular in nature, but it is essential for utility to represent them that way. The capacity to use such a simple representation is challenged by a lot of things such a chemistry. More and more physics challenge the ability to use the singular representation without empirical and heavy-handed modeling. The ability to use well-defined mathematical models as opposed to ad hoc modeling implies essential understanding that belies a science that is compelling. The better the equations, the better the understanding, which is the essence of science that should provide us faith in its findings.

An example of lower mathematical maturity can be seen in the field of solid mechanics. In solids, the mathematical theory is stunted by comparison to fluids. A clear part of the issue is the approach taken by the fathers of the field in not providing a clear path for combined analytical-numerical analysis as fluids had. The result of this is a numerical background that is completely left adrift of the analytical structure of the equations. In essence the only option is to fully resolve everything in the governing equations. No structural and systematic explanation exists for the key singularities in material, which is absolutely vital for computational utility. In a nutshell the notion of the regularized singularity so powerful in fluid mechanics is foreign. This has a dramatically negative impact on the capacity of modeling and simulation to have a maximal impact.

All of these principles apply quite well to a host of other fields. In my work the areas of radiation transport and plasma physics. The merging of mathematics and physical understanding in these areas is better than solid mechanics, but not as advanced as fluid mechanics. In many respects the theories holding sway in these fields have profitably borrowed from fluid mechanics, but not to the extent necessary for a thoroughly vetted mathematical-numerical modeling framework needed for ultimate utility. Both fields suffer from immense complexity and the mathematical modeling tries to steer understanding, but ultimately various factors are holding the field back. Not the least of these is an prevailing undercurrent and intent in modeling for the World to be a well-oiled machine prone to be precisely determined.

I would posit that one of the key aspects holding fields back from progress toward a fully utilitarian capability is the death grip that Newtonian-style determinism has upon our models for the World. Its stranglehold on the philosophy of solid mechanical modeling is nearly fatal and retards progress like a proverbial anchor. To the extent that it governs our understanding in other fields (i.e., plasma physics, turbulence,…), progress is harmed. In any practical sense the World is not deterministic and modeling it as such has limited if not, negative utility. It is time to release this concept as being a useful blueprint for understanding. A far more pragmatic and useful path is to focus much greater energy on understanding the degree of unpredictability inherent in physical phenomena.

The key to making everything work is an artful combination of physical understanding with a mathematical structure. The capacity of mathematics to explain and predict nature is profound and unremittingly powerful. In the case of the singularity it is essential for useful, faithful simulations that we may put confidence in. Moreover the proper mathematical structure can alleviate the need for ad hoc mechanisms, which naturally produce less confidence and lower utility. Even where the mathematics seemingly exists like incompressible flow and turbulence, the lack of a tidy theory that fails to reproduce certain properties limits progress in profound ways. When the mathematics is even more limited and does not provide a structural explanation for what is seen like in fracture and failure in fluids, the simulations become untethered and progress is shuttered by the gaps.

I suppose my real message is that the mathematical-numerical modeling book is hardly closed and complete. It represents very real work that is needed for progress. The current approach to modeling and simulation dutifully ignores this, and produces a narrative that simply presents the value proposition that all that is needed is a faster computer. A faster computer while useful and beneficial to science is not the long pole in the tent insofar as improving the capacity of mathematical-numerical modeling to become more predictive. Indeed the long pole in the tent may well be changing the narrative about the objectives from prediction back to fundamental understanding.

The title of the post is a tongue and cheek homage to the line from the Big Lebowski, a Coen Brothers masterpiece. Like the dude in the movie, a singularity is the essence of coolness and ease of use.

If you want something new, you have to stop doing something old

― Peter F. Drucker

 

Low-trust environments are filled with hidden agendas, a lot of political games, interpersonal conflict, interdepartmental rivalries, and people bad-mouthing each other behind their backs while sweet-talking them to their faces. With low trust, you get a lot of rules and regulations that take the place of human judgment and creativity; you also see profound disempowerment. People will not be on the same page about what’s important.

— Stephen Covey

Being thrust into a leadership position at work has been an eye-opening experience to say the least. It makes crystal clear a whole host of issues that need to be solved. Being a problem-solver at heart, I’m searching for a root cause for all the problems that I see. One can see the symptoms all around, poor understanding, poor coordination, lack of communication, hidden agendas, ineffective vision, and intellectually vacuous goals… I’ve come more and more to the view that all of these things, evident as the day is long are simply symptomatic of a core problem. The core problem is a lack of trust so broad and deep that it rots everything it touches.

Only those who dare to fail greatly can ever achieve greatly.

― Robert F. Kennedy 

What is the basis of the lack of trust and how can it be cured or at the very least ameliorated? Are we simply fated to live in a World where the trust in our fellow man is intrinsically low?

Failure is simply the opportunity to begin again, this time more intelligently.

— Henry Ford

First, it is beneficial to understand what is at stake. With trust firmly in hand people are unleashed, and new efficiencies are possible. The trust and faith in each other causes people to work better, faster and more effectively. Second-guessing is short-circuited. The capability to achieve big things is harnessed, and lofty goals can be achieved. Communication is easy and lubricated. Without trust and faith the impacts are completely opposite and harm the capacity for excellence, progress and achievement. Whole books are written on the virtues of trust (Stephen Covey’s Speed of Trust comes to mind). Trust is a game changer, and a great enabler. It is very clear that trust is coming we are in short supply of and its harming society as a whole. Its fingerprints at work leave deep bruises and make anyone focused on progress frustrated.

Distrust is like a vicious fire that keeps going and going, even put out, it will reignite itself, devouring the good with the bad, and still feeding on empty.

― Anthony Liccione

The causes of low trust are numerous and deeply engrained in the structure of society today. For example the pervasive greed and seeming profit motive in almost all things undermines any view that people are generous. A general opening ante in any interaction is the feeling that someone is trying to gain advantage by whatever means necessary. The Internet has undermined authority-making information (and disinformation) so ubiquitous that we’ve lost the ability to sift fact from fiction. Almost every institution in society is under attack from legitimacy. All interests are viewed with suspicion and corruption seemingly abounds. We’ve never had a greater capacity to communicate with one another, yet we understand less than ever.

I’ll touch more on the greed and corruption because I think they are real and corrosive in the extreme. The issue that the basic assumption of greed and corruption is wider than its actuality and causes a lot of needless oversight and bureaucracy that lays waste to efficiency. Of course greed is a very real thing and manifests itself in our corporate culture and even celebrated by the very people who are hurt the most. The rise of Donald Trump as a viable Politician is amble evidence of just how incredibly screwed up everything has gotten. How a mildly wealthy, greedy, reality show character could ever be considered as a viable President is the clearest sign of a very sick culture. It is masking a very real problem of a society that celebrates the rich while those rich systematically prey on the whole of society leeches. They claim to be helping society even while they damage our future to feed their hunger. The deeper physic wound is the feeling that everyone is so motivated leading to the broad-based lack of trust of your fellow man.

So where do I see this in work? The first thing is the incredibly short leash we are kept on and the pervasive micromanagement. We here words like “accountability” and “management assurance”, but its really “we don’t trust you at all”. Every single activity is burdened by oversight that acts to question and second-guess every decision and even the motivations behind them. Rather than everyone knowing what the larger aims, objective and goals and assuming that there is a broad based approach to solution, people assume that folks are out to waste and defraud. We impose huge costs in time; money and effort to assure that we don’t waste a dime or hour doing anything except what you are assigned to do. All of this oversight comes at a huge cost, and the expense of the oversight is actually the tip of the proverbial iceberg. The micromanagement is so deep that it kneecaps any and all ability to be agile and adaptive in how work is done. Plans have to be followed to a tee even when it is evident that the plans didn’t really match the reality that develops upon meeting the problem.

Suspicion ruins the atmosphere of trust in a team and makes it ineffective

― Sunday Adelaja

The micromanagement has even deeper impacts on the ability to combine, collaborate and envision broader perspectives. People’s work is closely scrutinized, planned and defined. Rather than engage in deep, broad perspectives in the nature of the work, people are encouraged if not implored to focus on the specific assignments to the exclusion of all else. I’ve seen such narrowness producing deeply pathological effects such as people seeing different projects they personally work on as being executed by a different people and incapable of expressing or articulating connections between the projects even when they are obvious. These impacts are crushing the level of quality in both the direct execution of the work and the development of people in the sense of having a deep, sustained career that builds toward personal growth.

In the overall execution of work another aspect of the current environment can be characterized as the proprietary attitude. Information hiding and lack of communication seem to be a growing problem even as the capacity for transmitting information grows. Various legal, or political concerns seem to outweigh the needs for efficiency, progress and transparency. Today people seem to know much less than they used to instead of more. People are narrower and more tactical in their work rather than broader and strategic. We are encouraged to simply mind our own business rather than seek a broader attitude. The thing that really suffers in all of this is the opportunity to make progress for a better future.

Don’t be afraid to fail. Don’t waste energy trying to cover up failure. Learn from your failures and go on to the next challenge. It’s ok to fail. If you’re not failing, you’re not growing.

— H. Stanley Judd

Milestones and reporting is an epitome of bad management and revolves completely around a lack of trust. Instead of being a tool for managing effort and lubricating the communication these tools are used to dumb down work, and assure low quality, low impact work as the standard of delivery. The reporting has to have marketing value instead of information and truth-value. It is used to sell the program and assure the image of achievement rather than provide an accurate picture of the status. Problems, challenges and issues tend to be soft-pedaled and deep sixed rather than discussed openly and deeply. Project planning in milestone are anchors against progress instead of aspirational goals. There is significant structure in the attitude toward goals that drives quality and progress away from objectives. This drive is the inability to accept failure as a necessary and positive aspect of the conduct of any work that is aggressive and progressive. Instead we are encouraged to always succeed and this encouragement means goals are defined to low and trivially achievable.

I’ve written before about preponderance of bullshit as a means of communicating work. Instead of honest and clear communication of information, we see communication of things that are constructed with the purpose of deceiving rewarded. Part of the issue is the inability for the system to accept failure, accept unexpected results as contributing to bullshit. Another matter that contributes to the amount of bullshit is the lack of expertise in the value system. True experts are not trusted, or simply viewed as having a hidden agenda. Notions of nuance that color almost anything an expert might tell you are simply not trusted. Instead we favor a simple and well-crafted narrative over the truth. It is much easier to craft fiction into a compelling message than a nuanced truth. Once this path is taken it is a quick trip to complete bullshit.

How do we fix any of this?

The simplest thing to do is value the truth, value excellence and cease rewarding the sort of trust-busting actions enumerated above. Instead of allowing slip-shod work to be reported as excellence we need to make strong value judgments about the quality of work, reward excellence, and punish incompetence. The truth and fact needs to be valued above lies and spin. Bad information needs to be identified as such and eradicated without mercy. Many greedy self-interested parties are strongly inclined to seed doubt and push lies and spin. The battle is for the nature of society. Do we want to live in a World of distrust and cynicism or one of truth and faith in one another? The balance today is firmly stuck at distrust and cynicism. The issue of excellence is rather pregnant. Today everyone is an expert, and no one is an expert with the general notion of expertise being highly suspected. The impact of such a milieu is absolutely damaging to the structure of society and the prospects for progress. We need to seed, reward and nurture excellence across society instead of doubting and demonizing it.

Of course deep within this value system is the concept of failure. Failure achieved while trying to do excellent good things must cease to be punished. Today failure is equivocated with fraud and is punished even when the objectives were good and laudable. This breeds all the bad things that are corroding society. Failure is absolutely essential for learning and the development of expertise. To be an expert is to have failed, and failed in the right way. If we want to progress societally, one needs to allow, even encourage failure. We have to stop the attempts to create a fail-safe system because fail-safe quickly becomes do nothing.

What do you do with a mistake: recognize it, admit it, learn from it, forget it.

— Dean Smith

Ultimately we need to conscientiously drive for trust as a virtue in how we approach each other. A big part of trust is the need for truth in our communication. The sort of lying, spinning and bullshit in communication does nothing but undermine trust, and empower low quality work. We need to empower excellence through our actions rather than simply declare things to be excellent by definition and fiat. Failure is a necessary element in achievement and expertise. It must be encouraged. We should promote progress and quality as a necessary outcome across the broadest spectrum of work. Everything discussed above needs to be based in a definitive reality and have actual basis in facts instead of simply bullshitting about it, or it only having “truthiness”. Not being able to see the evidence of reality in claims of excellence and quality simply amplifies the problems with trust, and risks devolving into a viscous cycle dragging us down instead of a virtuous cycle that lifts us up.

 

If you are afraid of failure you don’t deserve to be successful!

— Charles Barkley

There is only one thing that makes a dream impossible to achieve: the fear of failure.

― Paulo Coelho