Taking a new step, uttering a new word, is what people fear most.

― Fyodor Dostoyevsky

The title is a bit misleading so it could be concise. A more precise one would be “Progress is mostly incremental; then progress can be (often serendipitously) massive” Without accepting incremental progress as the usual, typical outcome, the massive leap forward is impossible. If incremental progress is not sought as the natural outcome of working with excellence, progress dies completely. The gist of my argument is that attitude and orientation is the key to making things better. Innovation and improvement are the result of having the right attitude and orientation rather than having a plan for it. You cannot schedule breakthroughs, but you can create an environment and work with an attitude that makes it possible, if not likely. The maddening thing about breakthroughs is their seemingly random nature, you cannot plan for them they just happen, and most of the time they don’t.

For me, the most important aspect of the work environment is the orientation toward excellence and progress. Is work focused on being “the best” or the best we can be? Are we trying to produce “state of the art” results, or are we trying to push the state of the art further? What is the attitude and approach to critique and peer review? What is the attitude toward learning, and adaptively seeking new connections between ideas? How open is the work to accepting, even embracing, serendipitous results? Is the work oriented toward building deep sustainable careers where “world class” expertise is a goal and resources are extended to achieve this end?

Increasingly when I honestly confront all these questions, the answers are troubling. There seems to be the attitude that all of this can be managed, but control of progress is largely an illusion. Usually the answers are significantly oriented away from those that would signify these values. Too often the answers are close to the complete opposite of the “right” ones. What we see is a broad aegis of accountability used to bludgeon the children of progress to death in their proverbial cribs. If accountability isn’t enough to kill progress, compliance is wheeled out as progress’ murder weapon. Used in combination we see advances slow to a crawl, and expertise fail to form where talent and potential was vast. The tragedy of our current system is lost futures first among human’s whose potential greatness is squandered, and secondly in the progress and immense knowledge they would have created. Ultimately all of this damage is heaped upon the future in the name of safety and security that feeds upon pervasive and malignant fear. We are too afraid as a culture to allow people the freedoms needed to be great and do great things.

So much of modern management seems to think that innovation is something to be managed for and everything can be planned. Like most things where you just try too damn hard, this management approach has exactly the opposite effect. We are actually unintentionally, but actively destroying the environment that allows progress, innovation and breakthroughs to happen. The fastidious planning does the same thing. It is a different thing than having a broad goal and charter that pushes toward a better tomorrow. Today we are expected to plan our research like we are building a goddamn bridge! It is not even remotely the same! The result is the opposite and we are getting less for every research dollar than ever before.

Without deviation from the norm, progress is not possible.

― Frank Zappa

In a lot of respects getting to an improved state is really quite simple. Two simple changes in how we plan and how we view success at work can make an enormous difference. First we need to always strive to improve, get better whether we are talking personally or in terms of our work. Secondly, we need to not simply be “state of the art” or “world class,” we need to advanced the state of the art, or define what it means to be world class. The driving aim is to strive to be the best and make things better as our default setting. The power of default setting is incredible. The default is so often the unconscious choice that setting the default may be the single most important decision commonly made. As soon as we accept that we, or our work are “good enough” and “fit to purpose” we have lost the battle for the future. The frequency of the default setting of “good enough” is sufficient to ensure that mediocrity creeps inevitably into the frame.

A goal ensures progress. But one gets much further without a goal.

― Marty Rubin

A large part of the problem with our environment is an obsession with measuring performance by the achievement of goals or milestones. Instead of working to create a super productive and empowering work place where people work exceptionally by intrinsic motivation, we simply set “lofty” goals and measure their achievement. The issue is the mindset implicit in the goal setting and measuring; this is the lack of trust in those doing the work. Instead of creating an environment and work processes that enable the best performance, we define everything in terms of milestones. These milestones and the attitudes that surround them sew the seeds of destruction, not because goals are wrong or bad, but because the behavior driven by achieving management goals is so corrosively destructive.

The result is loss of an environment that can enable the best results as a focus, and goal setting that becomes increasingly risk adverse. When goals and milestones are used to judge people, they start to set the bar lower to make sure they meet the standard. The better approach is to create the environment, culture and processes that enable the work to be the best, and reap the rewards that flow naturally. Moreover in the process of creating the environment, culture and process the workplace is happier, as well as higher performing. Intrinsic motivation is harnessed instead of crushed. Everyone benefits from a better workplace and better performance, but we lack the trust needed to do this. Setting goals and milestones simply over charges the achievement and leaves little or no room for the risk necessary for innovation. We find ourselves in a system where the innovation is killed by the lack of risk taking that milestone driven management creates.

So how does progress really work? The truth is that there are really very few major breakthroughs, and almost none of them are every planned. Most of the time people simply make incremental changes and improvements, which have small, but positive changes on what they work on. These are bricks in the wall and gentle nudges to the status quo. Occasionally these small positive changes cause something greater. Occasionally the little thing becomes something monumental and creates a massive improvement. The trick is that you typically can’t tell what little change will have the big impact in advance. Without looking for the small changes as a way of life, and a constant property, the next big thing never comes.

This is the trap of planning. You can’t plan breakthroughs and can’t schedule a better future. Getting to massive improvements is more about creating an environment of excellence, and continuous improvement than any sort of change agenda. The key to getting breakthroughs is to get really good people to work on improving the state of the art or state of the knowledge continuously. We need broad and expansive goals with aspirational character. Instead we have overly specific goals that simply ooze a deep distrust for those conducting the work. With the lack of trust and faith in how the work is done people retract to promising the sure thing, or simply the thing they have already accomplished. The death of progress is found by having a culture of simply implementing and staying at the state of the art or being world class.

The reasonable man adapts himself to the world: the unreasonable one persists in trying to adapt the world to himself. Therefore all progress depends on the unreasonable man.

― George Bernard Shaw

Lots of examples exist in the technical world whether it is new numerical methods, or technology (like GPS for example). Almost none of these sought to change the World, but they did by simply taking a key step over a threshold where the change became great. Social movements are another prime example.

. Take the fight for marriage equality as a great example of the small things leading to huge changes. A county clerk in New Mexico (Dona Ana where Las Cruces is located) stood up and granted marriage licenses to gay and lesbian citizens. This step along with other small actions across the country launched a tidal wave of change that culminated in making marriage equality the law for the entire nation.

So the difference is really simple and clear. You must be expanding the state of the art, or defining what it means to be world class. Simply being at the state of the art or world class is not enough. Progress depends on being committed and working actively at improving upon and defining state of the art and world-class work. Little improvements can lead to the massive breakthroughs everyone aspires toward, and really are the only way to get them. Generally all these things are serendipitous and depend entirely on a culture that creates positive change and prizes excellence. One never really knows where the tipping point is and getting to the breakthrough depends mostly on the faith that it is out there waiting to be discovered.

Be the change that you wish to see in the world.

― Mahatma Gandhi

Taking a new step, uttering a new word, is what people fear most.

Computing the solution to flows containing shock waves used to be exceedingly difficult, and for a lot of reasons it is now modestly difficult. Solutions for many problems may now be considered routine, but numerous pathologies exist and the limit of what is possible still means research progress are vital. Unfortunately there seems to be little interest in making such progress from those funding research, it goes in the pile of solved problems. Worse yet, there a numerous preconceptions about results, and standard practices about how results are presented that contend to inhibit progress. Here, I will outline places where progress is needed and how people discuss research results in a way that furthers the inhibitions.

I’ve written on this general topic before along with general advise on how to make good decisions in designing methods, https://williamjrider.wordpress.com/2015/08/14/evolution-equations-for-developing-improved-high-resolution-schemes-part-1/. In a nutshell, shocks (discontinuities) provide a number of challenges and some difficult realities to thetable. To do the best job means making some hard choices that often fly in the face of ideal circumstances. By making these hard choices you can produce far better methods for practical use. It often means sacrificing things that might be nice in an ideal linear world for the brutal reality of a nonlinear world. I would rather have something powerful and functional in reality than something of purely theoretical interest. The published literature seems to be opposed to this point-of-view with a focus on many issues of little practical importance.

It didn’t used to be like this. I’ve highlighted the work of Peter Lax before https://williamjrider.wordpress.com/2015/06/25/peter-laxs-philosophy-about-mathematics/, and it would be an understatement to say that his work paved the way for progress in compressible fluid mechanics. Other fields such as turbulence, solid mechanics, electro-magnetics have all suffered from the lack of similar levels of applied mathematical rigor and foundation. Despite this shining beacon of progress other fields have failed to build upon this example. Worse yet, the difficulty of extending Lax’s work is monumental. Moving into high dimensions invariably leads to instability and flow that begins to become turbulent, and turbulence is poorly understood. Unfortunately we are a long way from recreating Lax’s legacy in other fields (see e.g., https://williamjrider.wordpress.com/2014/07/11/the-2014-siam-annual-meeting-or-what-is-the-purpose-of-applied-mathematics/).

If one takes a long hard look at problems that pace our modeling and simulation, turbulence figures prominently. We don’t understand turbulence worth a damn. Our physical understanding is terrible and not sufficient to simply turn our understanding over to supercomputers to crush (see https://williamjrider.wordpress.com/2016/07/04/how-to-win-at-supercomputing/). In truth, this is an example where our computing hubris exceeds our intellectual grasp considerably. We need significantly greater modeling understanding to power progress. Such understanding is far too often assumed to exist where it does not. Progress in turbulence is stagnant and clearly lacks key conceptual advances necessary to chart a more productive path. It is vital to do far more than simply turn codes loose on turbulent problems and let great solutions come out because they won’t. Nonetheless, it is the path we are on. When you add shocks and compressibility to the mix, everything gets so much worse. Even the most benign turbulence is poorly understood much less anything complicated. It is high time to inject some new ideas into the study rather than continue to hammer away at the failed old ones. In closing this vignette, I’ll offer up a different idea: perhaps the essence of turbulence is compressible and associated with shocks rather than being largely divorced from these physics. Instead of building on the basis of the decisively unphysical aspects of incompressibility, turbulence might be better built upon a physical foundation of compressible (thermodynamic) flows with dissipative discontinuities (shocks) that fundamental observations call for and current theories cannot explain.

Further challenges with shocked systems occur with strong shocks where nonlinearity is ramped up to a level that exposes any lingering short-comings. Multiple materials are another key physical difficulty that exposes any solution methodology’s weaknesses to acute focus. Again and again the greatest rigor in simpler settings provide a foundation for good performance when things get more difficult. Methods that ignore a variety of difficult and seemingly unfortunate realities will underperform compared to those that confront these realities directly. Usually the methods that underperform simply add more dissipation to overcome things. The dissipation usually is added in a rather heavy-handed manner because it is unguided by theory and works in opposition to unpleasant realities. Rather than seeing these realities as being the result of being pessimistic, it is the result of pragmatism. The result of being irrationally optimistic is always worse than pragmatic realism.

Let’s get to one of the biggest issues that confounds the computation of shocked flows, accuracy, convergence and order-of-accuracy. For computing shock waves, the order of accuracy is limited to first-order for everything emanating from any discontinuity (Majda & Osher 1977). Further more nonlinear systems of equations will invariably and inevitably create discontinuities spontaneously (Lax 1973). In spite of these realities the accuracy of solutions with shocks still matters, yet no one ever measures it. The reasons why it matter are far more subtle and refined, and the impact of accuracy is less pervasive in its victory. When a flow is smooth enough to allow high-order convergence, the accuracy of the solution with high-order methods is unambiguously superior. With smooth solutions the highest order method is the most efficient if you are solving for equivalent accuracy. When convergence is limited to first-order the high-order methods effectively lower the constant in front of the error term, which is less efficient. One then has the situation where the gains with high-order must be balanced with the cost of achieving high-order. In very many cases this balance is not achieved.

What we see in the published literature is convergence and accuracy only being assessed for smooth problems where the full order of accuracy may be seen. In the cases that are actually driving the development of methods where shocks are present accuracy and convergence is ignored. If you look at the published papers and the examples, the order of accuracy is measured and demonstrated on smooth problems almost as a matter of course. Everyone knows that the order of accuracy cannot be maintained with a shock or discontinuity, and no one measures the solution accuracy or convergence. The problem is that these details still matter! You need convergent methods, and you have interest in the magnitude of the numerical error. Moreover there are still significant differences in these results on the basis of methodological differences. To up the ante, the methodological differences carry significant changes in the cost of solution. What one finds typically is a great deal of cost to achieve formal order of accuracy that provides very little benefit with shocked flows (see Greenough & Rider 2005, Rider, Greenough & Kamm 2007). This community in the open, or behind closed doors rarely confronts the implications of this reality. The result is a damper on all progress.

The standard for complex flow is well-known and documented before (i.e., “swirlier is better” https://williamjrider.wordpress.com/2014/10/22/821/). When combined with our appallingly poor understanding of turbulence, you have a perfect recipe for computing and selling complete bullshit (https://williamjrider.wordpress.com/2015/12/10/bullshit-is-corrosive/). The side-dish for the banquet of bullshit is the even broader use of the viewgraph norm (https://williamjrider.wordpress.com/2014/10/07/the-story-of-the-viewgraph-norm/) where nothing quantitative is used for comparing results. At its worst, the viewgraph norm is used in comparing results where an analytical solutions is available. So we have a case where an analytical solution is available to do a complete assessment of error and we ignore its utility perhaps only using it for plotting. What a massive waste! More importantly it masks problems that need attention.

Underlying this awful practice is a viewpoint that the details, and magnitude of the error does not matter. Nothing could be further from the truth, the details matter a lot and there are huge differences from method to method. All these differences are systematically swept under the proverbial rug. With shock waves one has a delicate balance between the sharpness of the shock and the creation of post-shock oscillations. Allowing a shock wave to be slightly broader can remove many pathologies and produce a cleaner looking solution, but also increases the error. Determining the relative quality of the solutions is left to expert pronouncements, and experts determine what is good and bad instead of the data. I’ve written about how to do this right several times before, and its not really difficult, https://williamjrider.wordpress.com/2015/01/29/verification-youre-doing-it-wrong/. What ends up being difficult is honestly confronting reality and all the very real complications it brings to the table. It turns out that most of us simply prefer to be delusional.

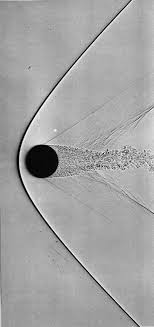In the end shocks are a well-trod field with a great deal of theoretical support for a host issues of broader application. If one is solving problems in any sort of real setting, the behavior of solutions is similar. In other words you cannot expect high-order accuracy almost every solution is converging at first-order (at best). By systematically ignoring this issue, we are hurting progress toward better, more effective solutions. What we see over and over again is utility with high-order methods, but only to a degree. Rarely does the fully rigorous achievement of high-order accuracy pay off with better accuracy per unit computational effort. On the other hand methods which are only first-order accurate formally are complete disasters and virtually useless practically. Is the sweet spot second-order accuracy? (Margolin and Rider 2002) Or just second-order accuracy for nonlinear parts of the solution with a limited degree of high-order as applied to the linear aspects of the solution? I think so.

Perfection is not attainable, but if we chase perfection we can catch excellence

Lax, Peter D. Hyperbolic systems of conservation laws and the mathematical theory of shock waves. Vol. 11. SIAM, 1973.

Majda, Andrew, and Stanley Osher. “Propagation of error into regions of smoothness for accurate difference approximations to hyperbolic equations.”Communications on Pure and Applied Mathematics 30, no. 6 (1977): 671-705.

Rider, William J., Jeffrey A. Greenough, and James R. Kamm. “Accurate monotonicity-and extrema-preserving methods through adaptive nonlinear hybridizations.” Journal of Computational Physics 225, no. 2 (2007): 1827-1848.

Greenough, J. A., and W. J. Rider. “A quantitative comparison of numerical methods for the compressible Euler equations: fifth-order WENO and piecewise-linear Godunov.” Journal of Computational Physics 196, no. 1 (2004): 259-281.

Margolin, Len G., and William J. Rider. “A rationale for implicit turbulence modelling.” International Journal for Numerical Methods in Fluids 39, no. 9 (2002): 821-841.

Simplicity is the ultimate sophistication.

― Clare Boothe Luce

When one is solving problems involving a flow of some sort, conservation principles are quite attractive since these principles follow nature’s “true” laws (true to the extent we know things are conserved!). With flows involving shocks and discontinuities, the conservation brings even greater benefits as the Lax-Wendroff theorem demonstrates (https://williamjrider.wordpress.com/2013/09/19/classic-papers-lax-wendroff-1960/). In a nutshell you have guarantees about the solution through the use of conservation form that are far weaker without it. A particular set of variables is the obvious variables because they arise naturally in conservation form. For fluid flow these are density, momentum and total energy. The most seemingly straightforward thing to do is use these same variables to discretize the equations. This is generally a bad choice and should be avoided unless one does not care about the quality of results.

While straightforward and obvious, the choice of using conserved variables is almost always a poor one, and far better results can be achieved through the use of primitive variables for most of the discretization and approximation work. This is even true if one is using characteristic variables (which usually imply some sort of entirely one-dimensional character). The primitive variables have simple and intuitive meaning physically, and often equate directly to what can be observed in nature (conservedvariables don’t). The beauty of primitive variables is that they trivially generalize to multiple dimensions in ways that characteristic variables do not. The other advantages are equally clear specifically the ability to extend the physics of the problem in a natural and simple manner. This sort of extension usually causes the characteristic approach to either collapse or at least become increasingly unwieldy. A key aspect to keep in mind at all times is that one returns to the conservation variables for the final approximation and update of the equations. Keeping the conservation form for the accounting of the complete solution is essential.

To keep the bulk of the discussion simple, I will focus on the Euler equations of fluid dynamics. These equations describe the conservations of mass, , momentum, and total energy, in one dimension. Even in this very simple setting the primitive variables are immensely useful as demonstrated by HT Huynh, in another of his massively under-appreciated papers. In this paper he masterfully covers the whole of the techniques and utility of primitive variables. Arguably, the use of primitive variables went mainstream with the papers of Colella and Woodward. In spite of the broad appreciation of that paper, the use of primitive variables in work is still more a niche than common practice. The benefits become manifestly obvious whether one is analyzing the equations (which is equivalent to the more complex variable set!), or discretizing the solutions.

Study the past if you would define the future.

― Confucius

The use of the “primitive variables” came from a number of different directions. Perhaps the earliest use of the term “primitive” came from meteorology in terms of the work of Bjerknes (1921) whose primitive equations formed the basis of early work in computing weather in an effort led by Jules Charney (1955). Another field to use this concept is the solution of incompressible flows. The primitive variables are the velocities and pressure, which is distinguished from the vorticity-streamfunction approach (Roache 1972). In two dimensions the vorticity-streamfunction solution is more efficient, but lacks simple connection to measurable quantities. The same sort of notion separates the conserved variables from the primitive variables in compressible flow. The use of primitive variables as an effective approach computationally may have begun in the computational physics work at Livermore in the 1970’s (see e.g., Debar). The connection of the primitive variables to classical analysis of compressible flows and simple physical interpretation also plays a role.

What are the primitive variables? The basic conserved variables form compressible fluid flow are density, , momentum, , and total energy, . Here the velocity is and the internal energy is . One also has the equation of state as the constitutive relation. Let’s take the Euler equations and rewrite them using the primitive variables, the conservations of mass, , momentum, and total energy, . Except for the energy equation, the expressions are simpler to work with, but this is the veritable tip of the proverbial iceberg.

What are the equations for the primitive variables? The primitive variables can be expressed and evolved using simpler equations, which are primarily evolution equations dependent on differentiability, which must be present for any sort of accuracy to be in play anyway. The mass equation is the same although one might expand the derivative, . The momentum equation is replaced by an equation of motion, . The energy equation could be replaced with a pressure equation, ( is the generalized isentropic derivative ) or an internal energy equation, . One can use either energy representation to good measure, or better yet, use both and avoid having to evaluate the equation of state. Moreover if one wants you can evaluate the difference between the pressure from the evolution equation and the state relation as an error measure.

How does on convert to the primitive variables, and convert back to the conserved variables? If one is interested in analysis of the conservative equations, then one linearizes the equations about a point, where is the vector of conserved varibles, and is the flux function. The matrix is the flux Jacobian. One does an eigenvalue decomposition, $ to analyze the equations. From this decomposition, , one can get the eigenvalues, , and the characteristic variables, . The analysis is difficult and non-intuitive with the conserved variables.

Here we get to the cool part of this whole thing, there is a much easier and more intuitive path through the primitive variables. One can get a matrix representation of the primitive variables which I’ll call in vector form, . One can get the terms in easily from the differential forms, and recognizing that , with being the speed of sound, the eigen-analysis is so simple that it can be done by hand (and it’s a total piece of cake for Mathematica). Using similar notation as the conserved form, . The first thing to note is that is exactly the same, i.e., the eigenvalues are identical. One then gets a result for the characteristics, that matches the textbooks, and that . All the differences in the transformation are bound up in the right eigenvectors and , and the ease of physical insight provided by the analysis.

Now we can elucidate how to move between these two forms, and even use the primitive variables for the analysis of the conserved form directly. Using Huynh’s paper as a guide and repeating the main results one defines a matrix of partial derivatives of the conserved variables, with respect to the primitive variables, , . This matrix then can be inverted into and we then may define an identity, , which might allow the conserved eigen-analysis to be executed in terms of the more convenient primitive variables. The eigenvalues of and are the same. We can get the left and right eigenvectors through and . All of this follows the simple application of the chain rule to the linearized versions of the governing equations.

The primitive variable idea can be extended in a variety of nifty and useful ways. One can augment the variable set in ways that can yield some extra efficiency to the solution by avoiding extra evaluations of the constitutive (or state) relations. This would most classically involve using both a pressure and energy equation in the system. Miller and Puckett provide a nice example of this technique in practice, building upon the work of Colella, Glaz and Ferguson where expensive equation of state evaluations are avoided. One must note that the system of equations being used to discretize the system is carrying redundant information that may have utility beyond efficiency.

One can go beyond this to add variables to the system of equations that are redundant, but carry information implicit in their approximation that may be useful in solving equations. One might add an equation for the specific volume of the fluid to compare with density. Similar things could be done with kinetic energy, vorticity, or entropy. In each case the redunency might be used to discover or estimate error or smoothness of the underlying solution and perhaps adapt the solution method on the basis of this information.

Using the primitive variables for discretization is almost as good as using characteristic variables in terms of solution fidelity. Generally if you can get away with 1-D ideas, the characteristic variables are unambiguously the best. The primitive variables are almost as good. The key is to use a local transformation to the primitive variables for the work of discretization even when your bookkeeping is all in conserved variables. Even if you are doing characteristic variables, the construction and use of them is enabled by primitive variables. The resulting expressions for the characteristics are simpler in primitive variables. Perhaps almost as important the expressions for the variables themselves are far more intuitively expressed in primitive variables.

A real source of power of the primitive variables comes when you extend past the simpler case of the Euler equations to things like magneto-hydrodynamics (MHD i.e., compressible magnetic fluids). Doing discretization of the MHD with conserved variables is a severe challenge and analysis of their mathematical characteristic structure can be a decent into utter madness. Doing the work in these more complex systems using the primitive variables is extremely advantageous. It is an approach that is far too often left out and the quality and fidelity of numerical methods suffers as a result.

Any intelligent fool can make things bigger, more complex, and more violent. It takes a touch of genius — and a lot of courage to move in the opposite direction.

― Ernst F. Schumacher

Lax, Peter, and Burton Wendroff. “Systems of conservation laws.”Communications on Pure and Applied mathematics 13, no. 2 (1960): 217-237.

Huynh, Hung T. “Accurate upwind methods for the Euler equations.” SIAM Journal on Numerical Analysis 32, no. 5 (1995): 1565-1619.

Colella, Phillip, and Paul R. Woodward. “The piecewise parabolic method (PPM) for gas-dynamical simulations.” Journal of computational physics 54, no. 1 (1984): 174-201.

Woodward, Paul, and Phillip Colella. “The numerical simulation of two-dimensional fluid flow with strong shocks.” Journal of computational physics54, no. 1 (1984): 115-173.

Van Leer, Bram. “Upwind and high-resolution methods for compressible flow: From donor cell to residual-distribution schemes.” Communications in Computational Physics 1, no. 192-206 (2006): 138.

Bjerknes, V. “The Meteorology of the Temperate Zone and the General Atmospheric CIRCULATION. 1.” Monthly Weather Review 49, no. 1 (1921): 1-3.

Charney, J. “The use of the primitive equations of motion in numerical prediction.” Tellus 7, no. 1 (1955): 22-26.

Roache, Patrick J. Computational fluid dynamics. Hermosa publishers, 1972.

DeBar, R. B. Method in two-D Eulerian hydrodynamics. No. UCID-19683. Lawrence Livermore National Lab., CA (USA), 1974.

Miller, Gregory Hale, and Elbridge Gerry Puckett. “A high-order Godunov method for multiple condensed phases.” Journal of Computational Physics128, no. 1 (1996): 134-164.

Colella, P., H. M. Glaz, and R. E. Ferguson. “Multifluid algorithms for Eulerian finite difference methods.” preprint (1996).