Progress, productivity, quality, independence, value, … Compliance kills almost everything I prize about work as a scientist. Compliance is basically enslavement to mediocrity and subservience to authority unworthy of being followed.

In the republic of mediocrity, genius is dangerous.

― Robert G. Ingersoll

Earlier this week I had an interesting exchange on Twitter with my friend Karen and a current co-worker Si. It centered around the fond memories that Karen and I have about working at Los Alamos. The gist of the conversation was that the Los Alamos we worked at was wonderful, even awesome. To me the experience at Los Alamos from 1989-1999 was priceless and the result of an impressively generous and technically masterful organization. I noted that it isn’t the way it was and that fact is absolutely tragic. Si countered that it’s still full of good people that are great to interact with. All of this can be true and not the slightest bit contradictory. Si tends to be positive all the time, which can be a wonderful characteristic, but I know what Los Alamos used to mean, and it causes me a great deal of personal pain to see the magnitude of the decline and damage we have done to it. The changes at Los Alamos have been done in the name of compliance, to bring an unruly institution to heel and conform to imposed mediocrity.

How the hell did we come to this point?

In relative terms, Los Alamos is still a good place largely because of the echos of the same culture that Karen and I so greatly benefited from. Organizational culture is a deep well to draw from. It shapes so much of what we see from different institutions. At Los Alamos it has formed the underlying resistance to the imposition of the modern compliance culture. On the other hand, my current institution is tailor made to complete compliance, even subservience to the demands of our masters. When those masters have no interest in progress, quality, or productivity, the result in unremitting mediocrity. This is the core of the discussion, our master’s prime directive is compliance, which bluntly and specifically means “don’t ever fuck up!” In this context Los Alamos is the king of the fuck-ups, and others simply keep places nose clean thus succeeding in the eyes of the masters..

The second half of the argument comes down to recognizing that accomplishment and productivity is never a priority in the modern world. This is especially true once the institutions realized that they could bullshit their way through accomplishment without risking the core value of compliance. Thus doing anything real and difficult is detrimental because you can more easily BS your way to excellence and not run the risk of violating the demands of compliance. In large part compliance assures the most precious commodity in the modern research institution, funding. Lack of compliance is punished by lack of funding. Our chains are created out of money.

In the end they will lay their freedom at our feet and say to us, Make us your slaves, but feed us.

― Fyodor Dostoyevsky

A large part of the compliance is lack of resistance to intellectually poor programs. There was once a time when the Labs helped craft the programs that fund them. With each passing year this dynamic breaks down, and the intellectual core of crafting well-defined programs to accomplish important National goals wanes. Why engage in the hard work of providing feedback when it threatens the flow of money? Increasingly the only sign of success is the aggregate dollar figure flowing into a given institution or organization. Any actual quality or accomplishment is merely coincidental. Why focus on excellence or quality when it is so much easier to simply generate a press release that looks good.

We make our discoveries through our mistakes: we watch one another’s success: and where there is freedom to experiment there is hope to improve.

― Arthur Quiller-Couch

This entire compliance dynamic is at the core of so many aspects dragging us into the mire of mediocrity. Instead of working to produce a dynamic focused on excellence, progress and impact, we simply focus on following rules and bullshitting something that resembles an expected product. Managing a top rate scientific or engineering institution is difficult and requires tremendous focus on the things that matter. Every bit of our current focus is driving us away from the elements of success. Our masters are incapable
of supporting hard-nosed, critical peer reviews, allowing failure to positively arise from earnest efforts, empowering people to think independently, and rewarding efforts essential for progress. At the heart of everything is an environment that revolves around
fear, and control. We have this faulty belief that we can manage everything to avoid any bad things ever happening. In the end the only way to do this is stop all progress and make sure no one ever accomplishes anything substantial.

So in the end make sure you get those TPS reports in on time. That’s all that really matters.

Disobedience is the true foundation of liberty. The obedient must be slaves.

― Henry David Thoreau

Any physical theory is always provisional, in the sense that it is only a hypothesis: you can never prove it. No matter how many times the results of experiments agree with some theory, you can never be sure that the next time the result will not contradict the theory.

― Stephen Hawking

Over the past few decades there has been a lot of sturm and drang around the prospect that computation changed science in some fundamental way. The proposition was that computation formed a new way of conducting scientific work to compliment theory, experiment/observation. In essence computation had become the third way for science. I don’t think this proposition stands the test of time and should be rejected. A more proper way to view computation is as a new tool that aids scientists. Traditional computational science is primarily a means of investigating theoretical models of the universe in ways that classical mathematics could not. Today this role is expanding to include augmentation of data acquisition, analysis, and exploration well beyond the capabilities of unaided humans. Computers make for better science, but recognizing that it does change science at all is important to make good decisions.

The key to my rejection of the premise that computation is a close examination of what science is. Science is a systematic endeavor to understand and organize knowledge of the universe in a testable framework. Standard computation is conducted in a systematic manner to conduct studies of the solution to theoretical equations, but the solutions always depend entirely on the theory. Computation also provides more general ways of testing theory and making predictions well beyond the approaches available prior to computation. Computation frees us of limitations for solving the equations comprising the theory, but nothing about the fundamental dynamic in play. The key point is that utilizing computation is as an enhanced tool set to conduct science in an otherwise standard way.

I suppose it is tempting, if the only tool you have is a hammer, to treat everything as if it were a nail.

― Abraham H. Maslow

Why is this discussion worth having now?

Some of the best arguments for the current obsession with exascale computing are couched in advertising computing as a new way of doing science that somehow is game changing. It just isn’t a game changer; computation is an incredible tool that opens new options for progress. Looking at computing, as simply a really powerful tool that enhances standard science just doesn’t sound as good or as compelling for generating money. The problem is that computing is just that, a really useful and powerful tool, and little more. The proper context for computing carries with it important conclusions about how it should be used, and how it should not be used, neither is evident in today’s common rhetoric. As with any tool, computation must be used correctly to yield its full benefits.

This correct use and full benefit is the rub with current computing programs. The current programs focus almost no energy on doing computing correctly. None. They treat computing as a good unto itself rather than treating it as a deep, skillful endeavor that must be completely entrained within the broader scientific themes. Ultimately science is about knowledge and understanding of the World. This can only come from two places: the observation of reality, and theories to explain those observations. We judge theory by how well it predicts what we observe. Computation only serves as a vehicle for more effectively apply theoretical models and/or wrangling our observations practically. Models are still the wellspring of human thought. Computation does little to free us from the necessity for progress to be based on human creativity and inspiration.

Observations still require human ingenuity and innovation to be achieved. This can take the form of the mere inspiration of measuring or observing a certain factor in the World. Another form is the development of measurement devices that allow measurements. Here is a place where computation is playing a greater and greater role. In many cases computation allows the management of mountains of data that are unthinkably large by former standards. Another way of changing data that is either complementary or completely different is analysis. New methods are available to enhance diagnostics or see effects that were previously hidden or invisible. In essence the ability to drag signal from noise and make the unseeable, clear and crisp. All of these uses are profoundly important to science, but it is science that still operates as it did before. We just have better tools to apply to its conduct.

One of the big ways for computation to reflect the proper structure of science is verification and validation (V&V). In a nutshell V&V is the classical scientific method applied to computational modeling and simulation in a structured, disciplined manner. The high performance computing programs being rolled out today ignore verification and validation almost entirely. Science is supposed to arrive via computation as if by magic. If it is present it is an afterthought. The deeper and more pernicious danger is the belief by many that modeling and simulation can produce data of equal (or even greater) validity than nature itself. This is not a recipe for progress, but rather a recipe for disaster. We are priming ourselves for believing some rather dangerous fictions.

This is a healthy attitude expressed by Einstein. Replace theory with computation and ask the same question then inquire whether our attitudes toward models and simulation are equally healthy?

You make experiments and I make theories. Do you know the difference? A theory is something nobody believes, except the person who made it. An experiment is something everybody believes, except the person who made it.

― Albert Einstein

The archetype of this thought process is direct numerical simulation (DNS). DNS is most prominently associated with turbulence, but the mindset presents itself in many fields. The logic behind DNS is the following: if we solve the governing equations without any modeling in a very accurate manner, the solutions are essentially exact. These very accurate and detailed solutions are just as good as measurements of nature. Some would contend that the data from DNS is better because it doesn’t have any measurement error. Many modelers are eager to use DNS data to validate their models, and eagerly await more powerful computers to expand the grasp of DNS to more complex situations. This entire mindset is unscientific and prone to the creation of bullshit. A big part of the problem is a lack of V&V with DNS, but the core issue is deeper. The belief that the equations are exact, not simply accepted models from currently accepted theory.

Let me explain why I would condemn such a potentially useful and powerful activity so strongly. The problem with DNS used in this manner is that it does include a model of reality. Of course this ignores the fact that the equations themselves are a model of reality. The argument behind DNS is that the equations being solved are unquestioned. This lack of questioning is itself unscientific on the face of it, but let me go on. Others will argue that the equations being solved have been formally validated, thus their validity for modeling reality established. Again, this has some truth to it, but the validation is invariably for quantities that may be observed directly, and generally statistically. In this sense the data being used from DNS is validated by inference, but not directly. Using such unvalidated data for modeling is dangerous (it may be useful too, but needs to be taken with a big grain of salt). The use of DNS data needs to exercise caution and be applied in a circumspect manner, not in evidence today.

Perhaps one of the greatest issues with the application of DNS is its failure to utilize V&V systematically. The first leap of faith with DNS believes that no modeling is happening. The equations being solved are not exact, but rather models of reality. Next the error associated with the numerical integration of the equations is rarely (to never) quantified simply assumed to be negligibly small. Even if we were to accept DNS as equivalent to experimental data, the error needs to be defined as part of the data set (in essence the error bar). Other uncertainties almost required for any experimental dataset are also lacking with DNS. The treatment of data from DNS should be higher than any experimental data reflecting the caution such artificial information should be used with. Instead, the DNS computations are treated with less caution. In this way standard practice today veers all the way into cavalier.

The deepest issue with current programs pushing forward on the computing hardware is their balance. The practice of scientific computing requires the interaction and application of great swathes of scientific disciplines. Computing hardware is a small component in the overall scientific enterprise and among the aspect least responsible for the success. The single greatest element in the success of scientific computing is the nature of the models being solved. Nothing else we can focus on has anywhere close to this impact. To put this differently, if a model is incorrect no amount of computer speed, mesh resolution or numerical accuracy can rescue the solution. This is the statement of how scientific theory applies to computation. Even if the model is unyieldingly correct, then the method and approach to solving the model is the next largest aspect in terms of impact. The damning thing about exascale computing is the utter lack of emphasis on either of these activities. Moreover without the application of V&V in a structured, rigorous and systematic manner, these shortcomings will remain unexposed.

In summary, we are left to draw a couple of big conclusions: computation is not a new way to do science, but rather an enabling tool for doing standard science better. If we want to get the most out of computing requires a deep and balanced portfolio of scientific activities. The current drive for performance with computing hardware ignores the most important aspects of the portfolio, if science is indeed the objective. If we want to get the most science out of computation, a vigorous V&V program is one way to inject the scientific method into the work. V&V is the scientific method and gaps in V&V reflect gaps in scientific credibility. Simply recognizing how scientific progress occurs and following that recipe can achieve a similar effect. The lack of scientific vitality in current computing programs is utterly damning.

A computer lets you make more mistakes faster than any other invention with the possible exceptions of handguns and Tequila.

― Mitch Ratcliffe

 

 

The problem with incompetence is its inability to recognize itself.

― Orrin Woodward

My wife has a very distinct preference in late night TV shows. First, the show cannot be on late night TV, she is fast asleep by 9:30 most nights. Secondly, she is quite loyal. More than twenty years ago she was essentially forced to watch late night TV while breastfeeding our newborn daughter. Conan O’Brien kept her laughing and smiling through many late night feedings. He isn’t the best late night host, but he is almost certainly the silliest. His shtick is simply stupid with a certain sophisticated spin. One of the dumb bits on his current show is “Why China is kicking our ass”. It features Americans doing all sorts of thoughtless and idiotic things on video with the premise being that our stupidity is the root of any loss of American hegemony. As sad as this might inherently be, the principle is rather broadly applicable and generally right on the money. The loss of preeminence nationally is more due to shear hubris; manifest overconfidence and sprawling incompetence on the part of Americans than anything being done by our competitors.

The conventional view serves to protect us from the painful job of thinking.

― John Kenneth Galbraith

High performance computing is no different. By our chosen set of metrics, we are losing to the Chinese rather badly through a series of self-inflicted wounds instead of superior Chinese execution. Nonetheless, we are basically handing the crown of international achievement to them because we have become so incredibly incompetent at intellectual endeavors. Today, I’m going to unveil how we have thoughtlessly and idiotically run our high performance computing programs in a manner that undermines our success. My key point is that stopping the self-inflicted damage is the first step toward success. One must take careful note that the measure of superiority is based on a benchmark that has no practical value. Having metric of success with no practical value is a large part of the underlying problem.

Never attribute to malevolence what is merely due to incompetence

― Arthur C. Clarke

As a starting point I’ll state that current program kicking off, the Exascale Computing Project is a prime example of how we are completely screwing things up. It is basically a lexicon of ignorance and anti-intellectual thought paving the way to international mediocrity. The biggest issue is the lack of intellectual depth in the whole basis of the program, “The USA must have the faster computer”. The fastest computer does not mean anything unless we know how to use it. The fastest computer does not matter if it is fastest at doing meaningless things, or it isn’t fast doing things that are important. The fastest computer is simply a tool in a much larger “ecosystem” of computing. This fastest computer is the modern day equivalent of the “missile gap” from the cold war, which ended up being nothing but a political vehicle.

If part of this ecosystem is unhealthy, the power of the tool is undermined. The extent to which it is undermined should be a matter of vigorous debate. This current program is inadvertently designed to further unbalance an ecosystem that has been under duress for decades. We have been focused on computer hardware for the past quarter of a century while failing to invest in physics, engineering, modeling and mathematics all essential to the utility of the tool of computing. We have starved innovation in the use of computing and the set of most impactful aspects of the computing ecosystem. The result is an intellectually hollow and superficial program that will be a relatively poor investment in terms of benefit to society for dollar spent. In essence the soul of computing is being lost. Our quest for exascale computing belies a program that is utterly and unremittingly hardware focused. This hardware focus is myopic in the extreme and starves the ecosystem of major elements of its health. These elements are the tie to experiments, modeling, numerical methods and solution algorithms. The key to Chinese superiority, or not is whether they are making the same mistakes as we are making. If they are, their “victory” is hollow; if they aren’t their victory will be complete.

If you conform, you miss all of the adventures and stand against the progress of society.

― Debasish Mridha

Scientific computing has been a thing for about 70 years being born during World War 2. During that history there has been a constant push and pull of capability of computers, software, models, mathematics, engineering, method and physics. Experimental work has been essential to keep computations tethered to reality. An advance in one area would spur the advances in another in a flywheel of progress. A faster computer would make new problems previously seeming impossible to solve suddenly tractable. Mathematical rigor may suddenly give people faith in a method that previously seemed ad hoc and unreliable. Physics might ask new questions counter to previous knowledge, or experiments would confirm or invalidate model applicability. The ability to express ideas in software allows algorithms and models to be used that may have been too complex with older software systems. Innovative engineering provides new applications for computing that extend the scope and reach of computing to new areas of societal impact. Every single one of these elements is subdued in the present approach to HPC, and robs the ecosystem of vitality and power. We have learned these lessons in the recent past, yet swiftly forgotten them when composing this new program.

Control leads to compliance; autonomy leads to engagement.

― Daniel H. Pink

This alone could be a recipe for disaster, but it’s the tip of the iceberg. We have been mismanaging and undermining our scientific research in the USA for a generation both at research institutions like Labs and our universities. Our National Laboratories are mere shadows of their former selves. When I look at how I am managed the conclusion is obvious: I am well managed to be compliant to a set of conditions that have nothing to do with succeeding technically. Good management is applied to following rules and basically avoid any obvious “fuck ups”. Good management is not applied to successfully executing a scientific program. This being the prime directive today, the entire scientific enterprise is under siege. The assault on scientific competence is broad-based and pervasive as expertise is viewed with suspicion rather than respect. Part of this problem is the lack of intellectual stewardship reflected in numerous empty thoughtless programs. The second piece is the way we are managing science. A couple of easy things engrained into the way we do things that lead to systematic underachievement is inappropriately applied project planning and intrusive micromanagement into the scientific process. The issue isn’t management per se, but its utterly inappropriate application and priorities that are orthogonal to technical achievement.

One of the key elements in the downfall of American supremacy in HPC is the inability to tolerate failure as a natural outgrowth of any high-end endeavor. Our efforts are simply not allowed to fail at anything lest it be seen as a scandal or waste of money. In the process we deny ourselves the high-risk, but high-payoff activities that yield great leaps forward. Of course a deep-seated fear is at the root of the problem. As a direct result of this attitude, we end up not trying very hard. Failure is the best way to learn anything, and if you aren’t failing, your aren’t learning. Science is nothing more than a giant learning exercise. The lack of failure means that science simply doesn’t get done. All of this is obvious, yet our management of science has driven failure out. It is evident across a huge expanse of scientific endeavors, and HPC is no different. The death of failure is also the death of accomplishment. Correcting this problem alone would allow for significantly greater achievement, yet our current governance attitude seems utterly incapable of making progress here.

Tied like a noose around a neck is the problem of short-term focus. The short-term focus is the twin of the “don’t fail” attitude. We have to produce results and breakthroughs on a quarterly basis. We have virtually no idea where we are going beyond an annual basis, and the long-term plans continually shift with political whims. This short-term myopic view is being driven harder with each passing year. We effectively have no big long-term goals as a nation beyond simple survival. Its like we have forgotten to dream big and produce any sort of inspirational societal goals. Instead we create big soulless programs in the place of big goals. Exascale computing is perfect example. It is a goal without a real connection to anything societally important and is crafted solely for the purpose of getting money. It is absolutely vacuous and anti-intellectual at its core by viewing supercomputing as a hardware-centered enterprise. Then it is being managed like everything else with relentless short-term focus and failure avoidance. Unfortunately, even if it succeeds, we will continue our tumble into mediocrity.

This tumble into mediocrity is fueled by an increasingly compliance oriented attitude toward all work. Instead of working to conduct a balanced and impactful program to drive the capacity of computing to impact the real World, our programs simply comply with the intellectually empty directives from above. There is no debate about how the programs are executed because PI’s and Labs are just interested in getting money. The program is designed to be funded instead of succeed, and the Labs don’t act as honest brokers any longer being primarily interested in filling their own coffers. In other words, the program is designed as a marketing exercise, not a science program. Instead of a flywheel of innovative excellence and progress we produce a downward spiral of compliance driven mediocrity serving intellectually empty and unbalanced goals. If everyone gets their money and can successfully fill out their time sheets and gets a paycheck, it is a success.

At the end of the Cold War in the early 1990’s the USA’s Nuclear Weapons’ Labs were in danger of a funding free fall. Nuclear weapons’ testing ended in 1992 and the prospect of maintaining the nuclear weapons’ stockpile without testing, loomed large. A science-based stockpile stewardship (SBSS) program was devised to serve as a replacement, and HPC was one of the cornerstones of the program. SBSS provided a backstop against financial catastrophe at the Labs and provided long-term funding stability. This HPC element in SBSS was the ASCI program (which became the ASC program as it matured). The original ASCI program was relentlessly hardware focused with lots of computer science, along with activities to port older modeling and simulation codes to the new computers. This should seem very familiar to anyone looking at the new ECP program. The ASCI program is the model for the current exascale program. Within a few years it became clear that ASCI’s emphasis on hardware and computer science was inadequate to provide modeling and simulation support for SBSS with sufficient confidence. Important scientific elements were added to ASCI including algorithm and method development, verification and validation, and physics model development as well as stronger ties to experimental programs. These additions were absolutely essential for success of the program. That being said, these elements are all subcritical in terms of support, but they are much better than nothing.

If one looks at the ECP program the composition and emphasis looks just like the original ASCI program without the changes made shortly into its life. It is clear that the lessons learned by ASCI were ignored or forgotten by the new ECP program. It’s a reasonable conclusion that the main lesson taken from ASC program was how to get money by focusing on hardware. Two issues dominate the analysis of this connection:

1. none of the lessons learned by ASC necessary to conduct science have been learned by the exascale program. The exascale program is designed like the original ASCI program and fails to implement any of the programmatic modifications necessary for applied success. It is reasonable to conclude that the program has no serious expectation of applied scientific impact. Of course they won’t say this, but actions do speak louder than words!
2. The premise that exascale computing is necessary for science is an a priori assumption that has been challenged repeatedly (see JASONS reviews for example). The unfunded and neglected aspects of modeling, methods and algorithms all provide historically validated means to answer these challenges. Rather than address these challenges, they were rejected out of hand and never technically addressed. We simply see an attitude that bigger is better by definition and its been sold more as a patriotic call to arms than a balanced scientific endeavor. It remains true that faster computers are better, if you do everything right, we are not supporting the activities to do everything right (V&V, experimental connection and model development being primal in this regard).

Beyond the troubling lack of learning from past mistakes other issues remain. Perhaps the most obviously damning aspect of our current programs is their lack of connection to massive national goals. We simply don’t have any large national goals beyond being “great” or being “#1”. The HPC program is a perfect example. The whole program is tied to simply making sure that the USA is #1. In the past when computing came of age, the supercomputer was merely a tool that demonstrated utility in accomplishing something important to the nation or the world. It was not an end unto itself. This assured a definite balance in how the HPC was executed because the success was measured by HPC’s impact on a goal beyond itself. Today there is no goal beyond the HPC and the supercomputing as an activity suffers greatly. It has no measure of success outside itself. Any science done by supercomputer is largely for marketing, and press release. Quite often the results have little or no importance aside from the capacity to generate a flashy picture to impress people who know little or nothing about science.

Taken in sufficient isolation the objectives of the exascale program are laudable. An exascale computer is useful if it can be reasonably used. The issue is that such a computer does not live in isolation; it exists in a complex trade space where other options exist. My premise has never been that better or faster computer hardware is inherently bad. My premise is that the opportunity cost associated with such hardware is too high. The focus on the hardware is starving other activities essential for modeling and simulation success. The goal of producing an exascale computer is not an objective of opportunity, but rather a goal that we should actively divest ourselves of. Gains in supercomputing are overly expensive and work to hamper progress in related areas simply by the implicit tax produced by how difficult the new computers are to use. Improvements in real modeling and simulation capability would be far greater if we invested our efforts in different aspects of the ecosystem.

The key to holding a logical argument or debate is to allow oneself to understand the other person’s argument no matter how divergent their views may seem.

― Auliq Ice

 

 

 

God save me from idealists.

― Jim Butcher

Coming up with detailed mathematical analysis, much less the solution of (partial) differential equations is extremely difficult. In the effort to progress on this important, but critically difficult task various simplifications and idealizations can make all the difference between success and failure. This difficulty highlights the power and promise of numerical methods for solving such equations because simplifications and idealizations are not absolutely necessary for solution. Nonetheless, much of the faith in a numerical method is derived by congruence of the solution numerically with analytical solutions. This process is known as verification and paly an essential role in helping to provide evidence of the credibility of numerical simulations. Our faith in the ability of numerical simulations to solve difficult problems is thus grounded to some degree by the scope and span of our analytical knowledge. This tie is important to both recognize and carefully control because of analytical knowledge is necessarily limited in ways that numerical methods should not be.

In developing and testing computational methods, we spend a lot of time working on solving the ideal equations for a phenomenon. This is true in fluids, plasma, and many other fields. These ideal equations are usually something that comes from the age of classical physics and mathematics. Most commonly these ideal equations are associated with the names of greats of science, Newton, Euler, Poincare. This near obsession is one of the greatest dangers to progress I can think of. The focus on the ideal is the consequence of some almost religious devotion to classical ideas, and deeply flawed. By focusing on the classical ideal equations many of the important, critical and interesting aspects of reality escape attention. We remain anchored to the past in a way that undermines our ability to master reality with modernity.

Whenever a theory appears to you as the only possible one, take this as a sign that you have neither understood the theory nor the problem which it was intended to solve.

― Karl R. Popper

These ideal equations are starting points for investigations of the physical world, and arose in an environment where analytical work was the only avenue for understanding. Simplicity and stripping away the complexities of reality were the order of the day. Today we are freed to a very large extent from the confines of analytical study by the capacity to approximate solutions to equations. We are free to study the universe as it actually is, and produce a deep study of reality. The analytical methods and ideas still have utility for gaining confidence in these numerical methods, but their lack of grasp on describing reality should be realized. Our ability to study the reality should be celebrated and be the center of our focus. Our seeming devotion to the ideal simply distracts us and draws attention from understanding the real World.

The more pernicious and harmful aspect of ideality was a reverence for divinity insolutions. The ideal equations are supposed to represent the perfect, and in a sense the “hand of God” working in the cosmos. As such they represent the antithesis of moderni
ty. As such they represent the inappropriate injection of religiosity into the study of reality. For this reason alone the ideal equations should be deeply suspect at a philosophical level. These sort of religious ideas should not be polluting the unfettered investigation of reality. More than this we can see that the true engine of beauty in the cosmos is removed from these equations. So much of what is extraordinary about the universe is the messiness driven by the second law of thermodynamics. This law takes many forms and always removes the ideal from the equations, and injects the hard, yet beautiful face of reality.

A thing can be fine on paper but utterly crummy in the field.

― Robert A. Heinlein

Not only are these equations suspect for philosophical reasons, they are suspect for the imposed simplicity of the time they are taken from. In many respects the ideal equations miss most of fruits of the last Century of scientific progress. We have faithfully extended our grasp of reality to include more and more “dirty” features of the actual physical World. To a very great extent the continued ties to the ideal contribute to the lack of progress in some very important endeavors. Perhaps no case more amply demonstrates this handicapping of progress as well as turbulence. Our continued insistence that turbulence is tied to the ideal nature of incompressibility is becoming patently ridiculous. It highlights that important aspects of the ideal are synonymous with the unphysical.

I have spoken out about the issues with incompressibility several times in the past (https://williamjrider.wordpress.com/2014/03/07/the-clay-prize-and-the-reality-of-the-navier-stokes-equations/, https://williamjrider.wordpress.com/2015/03/06/science-requires-that-modeling-be-challenged/, https://williamjrider.wordpress.com/2016/04/08/the-singularity-abides/, https://williamjrider.wordpress.com/2016/04/15/the-essential-asymmetry-in-fluid-mechanics/, https://williamjrider.wordpress.com/2016/09/27/the-success-of-computing-depends-on-more-than-computers/). Here I will simply reiterate these points from the perspective of the concept of ideal equations. Incompressibility is a simple and utterly ideal in the sense that no nontrivial flow is exactly incompressible (). Real and nontrivial flow fields are only approximately incompressible. It is important to recognize that approximate and exactly incompressible are very different at their core. Exactly incompressible flows are fundamentally unphysical and unrealizable in the real world. Put differently, they are absolutely pathological.

An important thing to recognize in this discussion is the number of important aspects of reality that are sacrificed with incompressibility. The list is stunning and gives a hint of the depth of the loss. Gone is the second law of thermodynamics unless viscous effects are present. Gone is causality. Gone are important nonlinearities. This approximation is taken to the extreme of being an unphysical constraint that produces a deeply degenerate system of equations. Of greater consequence is the demolition of physics that may be at the heart of explaining turbulence itself. The essence of turbulence needs a singularity formation to make sense of observations. This is at the core of the Clay Prize, yet in the derivation of the incompressible equations, the natural nonlinear process for singularity formation is removed by fiat. Incompressibility creates a system of equations that is simple and yet only a shadow of the more general equations it claims to represent. I fear it is an albatross about the neck of fluid mechanics.

There are other idealities that need to be overturned. In many corners of fluid mechanics symmetries are assumed. Many scientists desire that they should be maintained under all sorts of circumstances. They rarely ask whether the symmetry is maintained in the face of perturbations from the symmetry that would reasonably be expected to exist in reality (in fact it is absolutely unreasonable to assume perfect symmetry). Some assumptions are reasonable in some situations where the flows are stable, but other cases would destroy these symmetries for any realistic flow. Pushing a numerical method to maintain symmetry under such circumstances where the instability would grow should be abhorrent and avoided. In the physical actual universe the destruction of symmetry is the normal evolution of a system and preservation is rarely observed. As such expectations of symmetry preservation in all cases define an unhealthy community norm.

A great example of this sort of dynamic occurs in modeling stars that end their lives in an explosion like type II supernovas. The classic picture was a static spherical star that burned elements in a series of concentric spheres or increasing mass as one got deeper into the star. Eventually the whole process becomes unstable as the nuclear reactions shift from exothermic to endothermic when iron is created. We observe explosions in such stars, but the idealized stars would not explode. Even if we forced the explosion, the evolution of the post-explosion could not match important observational evidence that implied deep mixing of heavy elements into the expanding envelope of the star.

It is a place where the idealized view stood in the way of progress of decades and the release of ideality allowed progress and understanding. Once these extreme symmetries were released and the star was allowed to rotate, have magnetic fields, and mix elements across the concentric spheres models and simulations started to match observations. We got exploding stars; we got the deep mixing necessary for both the explosion itself and the post explosion evolution. The simulations began to explain what we saw in nature. The process of these exploding stars is essential for the understanding of the universe because such stars are the birthplace of the matter that our World is built from. When things were more ideal the simulations failed to a very large extent.

This sort of issue appears over and over in science. Time and time again, the desire to study things in an ideal manner acts to impede the unveiling of reality. By now we should know better, but it is clear that we don’t. The idea of sustaining the ideal equations and evolution as the gold standard is quite strong. Another great example of this is the concept of kinetic energy conservation. Many flows and numerical methods are designed to exactly conserve kinetic energy. This only occurs in the most ideal of circumstances when flows have no natural dissipation (itself deeply unphysical) while retaining well-resolved smooth structure. So the properties are only seen in flows that are unphysical. Many believe that such flows should be exactly preserved as the foundation for numerical methods. This belief is somehow impervious to the observation that such flows are utterly unphysical and could never be observed in reality. It is difficult to square this belief system with the desire to model anything practical.

We need to recognize the essential tension between the need to test methods using the solution to idealized equations with the practical simulation of reality. We need to free ourselves of the limiting aspects of the mindset around the ideal equations. The important aspect of matching solutions to ideal equations must be acknowledged without imposing unphysical limits on the simulation. The imperative for numerical methods is modeling reality. To match aspects of the ideal equations solution many sacrifice physical aspect of numerical methods. Modeling reality should always be the preeminent concern for the equations and the methods for solution. Numerical methods unleash many of the constraints that analytical approaches abide by and these should be taken advantage of to a maximal degree.

Quite frequently, the way that numerical methods developers square their choices is an unfortunate separation of modeling from the numerical solutions. In some cases the choice that is followed is the philosophy where the ideal equations are solved along with the explicit modeling of any non-ideal physics. As such the numerical method is desired to be unwaveringly true to the ideal equations. Quite often the problem with this approach is that the non-ideal effects are necessary for the stability and quality of the solution. Moreover the coupling between the numerical solution and modeling is not clean, and the modeling can’t be ignored in the assessment of the numerical solution.

A great example of this dichotomy is turbulent fluid mechanics and it’s modeling. It is instructive to explore the issues surrounding the origin of the models with connections to purely numerical approaches. There is the classical thinking about modeling turbulence that basically comes down to solving the ideal equations as perfectly as possible, and modeling the entirety of turbulence with additional models added to the ideal equations. It is the standard approach and by comparison to many other areas of numerical simulation, a relative failure. Nonetheless this approach is followed with almost a religious fervor. I might surmise that the lack of progress in understanding turbulence is somewhat related to the combination of adherence to a faulty basic model (incompressibility) and the solution approach that supposes that all the non-ideal physics can be modeled explicitly.

It is instructive in closing to peer more keenly at the whole turbulence modeling problem. A simple, but very successful model for turbulence is the Smagorinsky model originally devised for climate and weather modeling, but forming the foundation for the practice of large eddy simulation (LES). What is under appreciated about the Smagorinsky model is its origins. This model was originally created as a way of stabilizing shock calculations by Robert Richtmyer and applied to an ideal differencing method devised by John Von Neumann. The ideal equation solution without Richtmyer’s viscosity was unstable and effectively useless. With the numerically stabilizing term added to the solution, the method was incredibly powerful and forms the basis of shock capturing. The same term was then added to weather modeling to stabilize those equations. It did just that and remarkably it suddenly transformed into a “model” for turbulence. In the process we lost the role it played for numerical stability, but also the strong and undeniable connection between the entropy generated by a shock and observed turbulence behavior. This connection was then systematically ignored because the unphysical incompressible equations we assume turbulence is governed by do not admit shocks. In this lack perspective we find the recipe for lack of progress. It is too powerful for a connection not to be present. Such connections creates issues that undermine some core convictions in the basic understanding of turbulence that seem too tightly held to allow the lack of progress to question.

We cannot become what we need by remaining what we are.

― John C. Maxwell

 

 

What’s measured improves

― Peter F. Drucker

In area of endeavor standards of excellence are important. Numerical methods are no different. Every area of study has a standard set of test problems that researchers can demonstrate and study their work on. These test problems end up being used not just to communicate work, but also test whether work has been reproduced successfully or compare methods. Where the standards are sharp and refined the testing of methods has a degree of precision and results in actionable consequences. Where the standards are weak, expert judgment reigns and progress is stymied. In shock physics, the Sod shock tube (Sod 1978) is such a standard test. The problem is effectively a “hello World” problem for the field, but suffers from weak standards of acceptance focused on expert opinion of what is good and bad without any unbiased quantitative standard being applied. Ultimately, this weakness in accepted standards contributes to stagnant progress we are witnessing in the field. It also allows a rather misguided focus and assessment of capability to persist unperturbed by results (standards and metrics can energize progress, https://williamjrider.wordpress.com/2016/08/22/progress-is-incremental-then-it-isnt/).

Sod’s shock tube is an example of a test problem being at the right time in the right place. It was published right at the nexus of progress in hyperbolic PDE’s, but before breakthroughs were well publicized. The article introduced a single problem applied to a large number of methods all of which performed poorly in one way or another. The methods were an amalgam of old and new methods demonstrating the general poor state of affairs for shock capturing methods in the late 1970’s. Since its publication is has become the opening ante for a method to demonstrate competence in computing shocks. The issues with this problem were highlighted in an earlier post, https://williamjrider.wordpress.com/2016/08/18/getting-real-about-computing-shock-waves-myth-versus-reality/, where a variety of mythological thoughts are applied to computing shocks.

This problem is a very idealized shock problem in one dimension that is amenable to semi-analytical solution. As a result an effectively exact solution may be obtained via solution of nonlinear equations. The evaluation of the exact solution appropriately for comparison with numerical solutions is itself slightly nontrivial. The analytical solution needs to be properly integrated over the mesh cells to represent the correct integrated control volume values (more over this integration needs to be done for the correct conserved quantities). Comparison is usually done via the primitive variables, which may be derived from the conserved variable using standard techniques (I wrote about this a little while ago https://williamjrider.wordpress.com/2016/08/08/the-benefits-of-using-primitive-variables/ ). A shock tube is the flow that is results when two semi-infinite slabs of gas at different state conditions are held separately. They are then allowed to interact and a self-similar flow is created. This flow can contain all the basic compressible flow structures, shocks, rarefactions, and contact discontinuities.

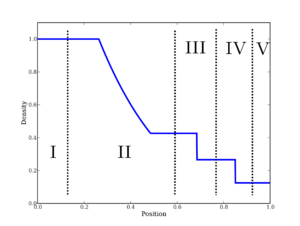Specifically, Sod’s shock tube (https://en.wikipedia.org/wiki/Sod_shock_tube) has the following conditions: in a one dimensional domain filled with an ideal gamma law gas, , , the domain is divided into two equal regions; on , ; on , . The flow is described by the compressible Euler equations (conservation of mass, , momentum and energy ), and an equation of state, . At time zero the flow develops a self-similar structure with a right moving shock followed by a contact discontinuity, and a left moving rarefaction (expansion fan). This is the classical Riemann problem. The solution may be found through semi-analytical means solving a nonlinear equation defined by the Rankine-Hugoniot relations (see Gottlieb and Groth for a wonderful exposition on this solution via Newton’s method).

The crux of the big issue with how this problem is utilized is that the analytical solution is not used for more than display in plotting comparisons with numerical solutions. The quality of numerical solutions is then only assessed qualitatively. This is a huge problem that directly inhibits progress. This is a direct result of having no standard beyond expert judgment on the quality. It leads to the classic “hand waving” argument for the quality of solutions. Actual quantitative differences are not discussed as part of the accepted standard. The expert can deftly focus on the parts of the solution they want to and ignore the parts that might be less beneficial to their argument. Real problems can persist and effectively be ignored (such as the very dissipative nature of some very popular high-order methods). Under this lack of standard relatively poorly performing methods can retain a high level of esteem while better performing methods are effectively ignored.

With all these problems, why does this state of affairs persist year after year? The first thing to note is that the standard of expert judgment is really good for experts. The expert can rule by asserting their expertise creating a bit of a flywheel effect. For experts whose favored methods would be exposed by better standards, it allows their continued use with relative impunity. The experts are then gate keepers for publications and standards, which tends to further the persistence of this sad state of affairs. The lack of any standard simply energizes the status quo and drives progress into hiding.

The key thing that has allowed this absurdity to exist for so long is the loss of accuracy associated with discontinuous solutions. For nonlinear solutions of the compressible Euler equations, high order accuracy is lost in shock capturing. As a result the designed order of accuracy for a computational method cannot be measured with a shock tube solution. As a result, one of the primary aims of verification is not achieved using this problem. One must always remember that order of accuracy is the confluence of two aspects, the method and the problem. Those stars need to align for the order of accuracy to be delivered.

Order of accuracy is almost always shown in results for other problems where no discontinuity exists. Typically a mesh refinement study, error norms, order of accuracy is provided as a matter of course. The same data is (almost) never shown for Sod’s shock tube. For discontinuous solutions the order of accuracy is (less than one). Ideally, the nonlinear features of the solution (shocks and expansions) converge at first-order, and the linearly degenerate feature (shears and contacts) converge at less than first order based on the details of the method (see the paper by Aslam, Banks and Rider (me). The core of the acceptance of the practice of not showing the error or convergence for shocked problems is the lack of differentiation of methods due to similar convergence rates for all methods (if they converge!). The relative security offered by the Lax-Wendroff theorem further emboldens people to ignore things (the weak solution guaranteed by it has to be entropy satisfying to be the right one!).

This is because the primal point of verification cannot be satisfied, but other aspects are still worth (or even essential) to pursue. Verification is also all about error estimation, and when the aims of order verification cannot be achieved, this becomes a primary concern. What people do not report and the aspect that is missing from the literature is the relatively large differences in error levels from different methods, and the impact of these differences practically. For most practical problems, the design order of accuracy cannot be achieved. These problems almost invariably converge at the lower order, but the level of error from a numerical method is still important, and may vary greatly based on details. In fact, the details and error levels actually have greater bearing on the utility of the method and its efficacy pragmatically under these conditions.

For all these reasons the current standard and practice with shock capturing methods are doing a great disservice to the community. The current practice inhibits progress by hiding deep issues and failing to expose the true performance of methods. Interestingly the source of this issue extends back to the inception of the problem by Sod. I want to be clear that Sod wasn’t to blame because none of the methods available to him were acceptable, but within 5 years very good methods arose, but the manner of presentation chosen originally persisted. Sod on showed qualitative pictures of the solution at a single mesh resolution (100 cells), and relative run times for the solution. This manner of presentation has persisted to the modern day (nearly 40 years almost without deviation). One can travel through the archival literature and see this pattern repeated over and over in an (almost) unthinking manner. The bottom line is that it is well past time to do better and set about using a higher standard.

At a bare minimum we need to start reporting errors for these problems. This ought to not be enough, but it is an absolute minimum requirement. The problem is that the precise measurement of error is prone to vary due to details of implementation. This puts the onus on the full expression of the error measurement, itself an uncommon practice. It is uncommonly appreciated that the difference between different methods is actually substantial. For example in my own work with Jeff Greenough, the error level for the density in Sod’s problem between fifth order WENO, and a really good second-order MUSCL method is a factor of two in favor of the second-order method! (see Greenough and Rider 2004, the data is given in the tables below from the paper). This is exactly the sort of issue the experts are happy to resist exposing. Beyond this small step forward the application of mesh refinement with convergence testing should be standard practice. In reality we would be greatly served by looking at the rate of convergence to problems feature-by-feature. We could cut up the problem into regions and measure the error and rate of convergence separately for the shock, rarefaction and contact. This would provide a substantial amount of data that could be used to measure quality of solutions in detail and spur progress.

Two tables of data from Greenough and Rider 2004 displaying the density error for Sod’s problem (PLMDE = MUSCL).

We still use methods quite commonly that do not converge to the right solution for discontinuous problems (mostly in “production” codes). Without convergence testing this sort of pathology goes undetected. For a problem like Sod’s shock tube, it can still go undetected because the defect is relatively small. Usually it is only evident when the testing is on a more difficult problem with stronger shocks and rarefactions. Even then it is something that has to be looked for showing up as reduced convergence rates, or the presence of constant un-ordered error in the error structure, instead of the standard . This subtlety is usually lost in a field where people don’t convergence test at all unless they expect full order of accuracy for the problem.

Now that I’ve thrown a recipe for improvement out there to consider, I think it’s worthwhile to defend expert judgment just a bit. Expertise has its role to play in progress. There are aspects of science that are not prone to measurement, science is still a human activity with tastes and emotion. This can be a force of good and bad, the need for dispassionate measurement is there as a counter-weight to the worst instincts of mankind. Expertise can be used to express a purely qualitative assessment that can make the difference between something that is merely good and great. Expert judgment can see through complexity to remediate results into a form with greater meaning. Expertise is more of a tiebreaker than the deciding factor. The problem today is that current practice means all we have is expert judgment and this is a complete recipe for the status quo and an utter lack of meaningful progress.

The important outcome from this discussion is crafting a path forward that makes the best use of our resources. Apply appropriate and meaningful metrics to the performance of methods and algorithms to make progress or lack of it concrete. Reduce, but retain the use of expertise and apply it to the qualitative aspects of results. The key to doing better is striking an appropriate balance. We don’t have it now, but getting to an improved practice is actually easy. This path is only obstructed by the tendency of the experts to hold onto their stranglehold.

An expert is someone who knows some of the worst mistakes that can be made in his subject, and how to avoid them.

― Werner Heisenberg

Historical montage of Sod shock tube results from Sod 1978, Harten 1983, Huynh 1996, Jiang and Shu 1996.  First Sod’s result for perhaps the best performing method from his paper (just expert judgment on my part LOL).

Harten, Ami. “High resolution schemes for hyperbolic conservation laws.”Journal of computational physics 49, no. 3 (1983): 357-393.

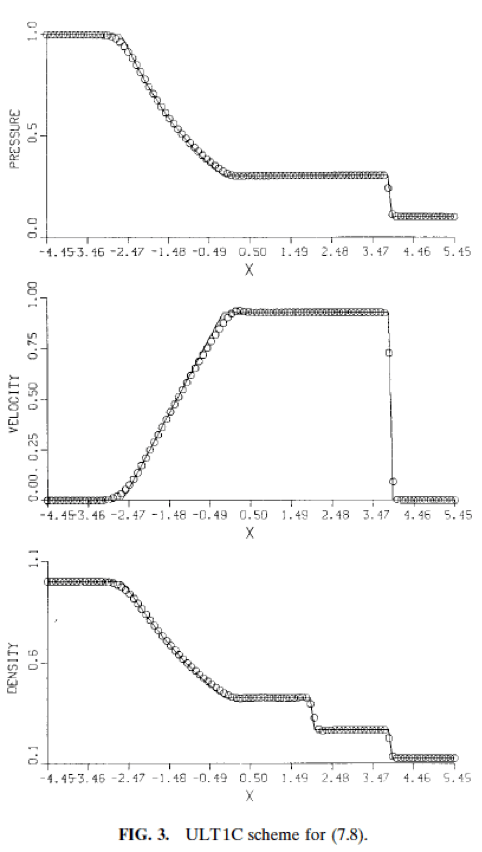
Suresh, A., and H. T. Huynh. “Accurate monotonicity-preserving schemes with Runge–Kutta time stepping.” Journal of Computational Physics 136, no. 1 (1997): 83-99.

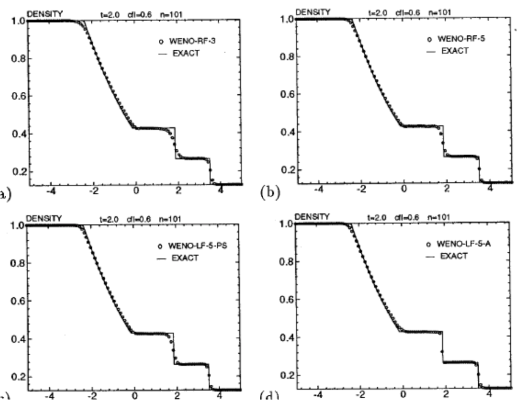
Jiang, Guang-Shan, and Chi-Wang Shu. “Efficient Implementation of Weighted ENO Schemes.” Journal of Computational Physics 126, no. 1 (1996): 202-228.

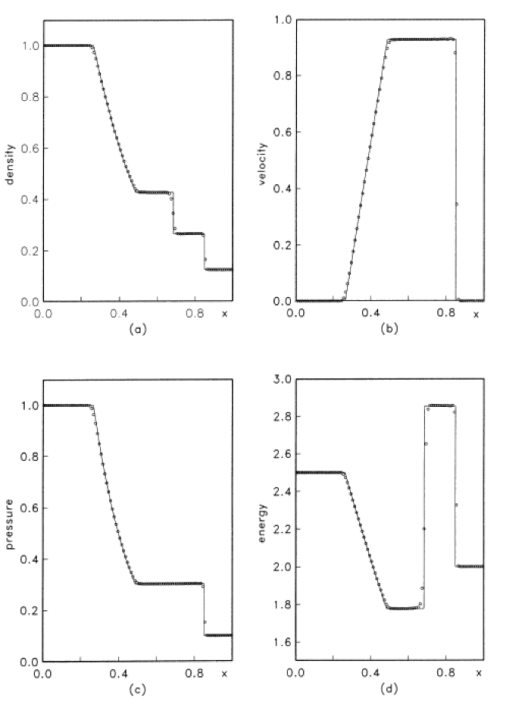
Sod, Gary A. “A survey of several finite difference methods for systems of nonlinear hyperbolic conservation laws.” Journal of computational physics 27, no. 1 (1978): 1-31.

Gottlieb, J. J., and C. P. T. Groth. “Assessment of Riemann solvers for unsteady one-dimensional inviscid flows of perfect gases.” Journal of Computational Physics 78, no. 2 (1988): 437-458.

Banks, Jeffrey W., T. Aslam, and W. J. Rider. “On sub-linear convergence for linearly degenerate waves in capturing schemes.” Journal of Computational Physics 227, no. 14 (2008): 6985-7002.

Greenough, J. A., and W. J. Rider. “A quantitative comparison of numerical methods for the compressible Euler equations: fifth-order WENO and piecewise-linear Godunov.” Journal of Computational Physics 196, no. 1 (2004): 259-281.