Von Neumann told Shannon to call his measure entropy, since “no one knows what entropy is, so in a debate you will always have the advantage.

― Jeremy Campbell

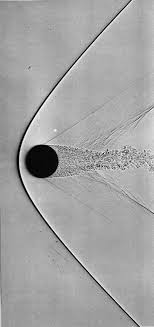Too often in seeing discourse about numerical methods, one gets the impression that dissipation is something to be avoided at all costs. Calculations are constantly under attack for being too dissipative. Rarely does one ever hear about calculations that are not dissipative enough. A reason for this is the tendency for too little dissipation to cause outright instability contrasted with too much dissipation with low-order methods. In between too little dissipation and instability are a wealth of unphysical solutions, oscillations and terrible computational results. These results may be all too common because of people’s standard disposition toward dissipation. The problem is that too few among the computational cognoscenti recognize that too little dissipation is as poisonous to results as too much (maybe more).

Why might I say that it is more problematic than too much dissipation? A big part of the reason is the nature physical realizability of solutions. A solution with too much dissipation is utterly physical in the sense that it can be found in nature. The solutions with too little dissipation more often than not are not found in nature. This is not because those solutions are unstable, but rather solutions that are stable, and have some dissipation; however, they simply aren’t dissipative enough to match natural law. What many do not recognize is that natural systems actually produce a large amount of dissipation without regard to the size of the mechanisms for explicit dissipative physics. This is both a profound physical truth, and the result of acute nonlinear focusing. It is important for numerical methods to recognize this necessity. Furthermore, this fact of nature reflects an uncomfortable coming together of modelling and numerical methods that many simply choose to ignore as an unpleasant reality.

In this house, we obey the laws of thermodynamics!

– Homer Simpson

Entropy stability is an increasingly important concept in the design of robust, accurate and convergent methods for solving systems defined by nonlinear conservation laws (see Tadmor 2016) The schemes are designed to automatically satisfy an entropy inequality that comes from the second law of thermodynamics, . Implicit in the thinking about the satisfaction of the entropy inequality is a view that approaching the limit of $latex d S / d t = 0$ as viscosity becomes negligible (i.e., inviscid) is desirable. This is a grave error in thinking about the physical laws of direct interest, as the solution of conservation laws does not satisfy this limit when flows are inviscid. Instead the solutions of interest (i.e., weak solutions with discontinuities) in the inviscid limit approach a solution where the entropy production is proportional to variation in the large scale solution cubed, . This scaling appears over and over in the solution of conservation laws including Burgers’ equation, the equations of compressible flow, MHD, and incompressible turbulence (Margolin & Rider, 2001). The seeming universality of these relations and their implications for numerical methods are discussed below in more detail, but follow the profound implications turbulence modelling are explored in detail for implicit LES modelling (our book edited by Grinstein, Margolin & Rider, 2007). Valid solutions will invariably produce the inequality, but the route to achievement varies greatly.

The satisfaction of the entropy inequality can be achieved in a number of ways and the one most worth avoiding is oscillations in the solution. Oscillatory solutions from nonlinear conservation laws are as common as they are problematic. In a sense, the proper solution is strong attractor for solutions and solutions will adjust to produce the necessary amount of dissipation in the solution. One vehicle for entropy production is oscillations in the solution field. Such oscillations are unphysical and can result in a host of issues undermining other physical aspects of the solution such as positivity of quantities such as density and pressure. They are to be avoided to whatever degree possible. If explicit action isn’t taken to avoid oscillations, one should expect them to appear.

There ain’t no such thing as a free lunch.

― Pierre Dos Utt

A more proactive approach to dissipation leading to entropy satisfaction is generally desirable. Another path toward entropy satisfaction is offered by numerical methods in control volume form. For second-order numerical methods the analysis of the approximation via the modified equation methodology unveils nonlinear dissipation terms that provide the necessary form for satisfying the entropy inequality via a nonlinearly dissipative term in the truncation error. This truncation error takes the form , which integrates to replicate inviscid dissipation as a residual term in the “energy” equation, . This term comes directly from being in conservation form and disappears when the approximation is in non-conservative from. In large part the overly large success of these second-order methods is related to this character.

Other options to add this character to solutions may be achieved by an explicit nonlinear (artificial) viscosity or through a Riemann solver. The nonlinear hyperviscosities discussed before on this blog work well. One of the pathological misnomers in the community is the belief that the specific form of the viscosity matters. This thinking infests direct numerical simulation (DNS) as it perhaps should, but the reality is that the form of dissipation is largely immaterial to establishing physically relevant flows. In other words inertial range physics does not depend upon the actual form or value of viscosity its impact is limited to the small scales of the flow. Each approach has distinct benefits as well as shortcomings. The key thing to recognize is the necessity of taking some sort of conscious action to achieve this end. The benefits and pitfalls of different approaches are discussed and recommended actions are suggested.

Enforcing the proper sort of entropy production through Riemann solvers is another possibility. A Riemann solver is simply a way of upwinding for a system of equations. For linear interaction modes the upwinding is purely a function of the characteristic motion in the flow, and induces a simple linear dissipative effect. This shows up as a linear even-order truncation error in modified equation analysis where the dissipation coefficient is proportional to the absolute value of the characteristic speed. For nonlinear modes in the flow, the characteristic speed is a function of the solution, which induces a set of entropy considerations. The simplest and most elegant condition is due to Lax, which says that the characteristics dictate that information flows into a shock. In a Lagrangian frame of reference for a right running shock this would look like, with being the sound speed. It has a less clear, but equivalent form through a nonlinear sound speed, . The differential term describes the fundamental derivative, which describes the nonlinear response of the sound speed to the solution itself. This same condition can be seen in a differential form and dictates some essential sign conventions in flows. The key is that these conditions have a degree of equivalence. The beauty is that the differential form lacks the simplicity of Lax’s condition, but establishes a clear connection to artificial viscosity.

The key to this entire discussion is realizing that dissipation is a fact of reality. Avoiding it is simply a demonstration of an inability to confront the non-ideal nature of the universe. This is simply contrary to progress and a sign of immaturity. Let’s just deal with reality.

The law that entropy always increases, holds, I think, the supreme position among the laws of Nature. If someone points out to you that your pet theory of the universe is in disagreement with Maxwell’s equations — then so much the worse for Maxwell’s equations. If it is found to be contradicted by observation — well, these experimentalists do bungle things sometimes. But if your theory is found to be against the second law of thermodynamics I can give you no hope; there is nothing for it but to collapse in deepest humiliation.

– Sir Arthur Stanley Eddington

References

Tadmor, E. (2016). Entropy stable schemes. Handbook of Numerical Analysis.

Margolin, L. G., & Rider, W. J. (2002). A rationale for implicit turbulence modelling. International Journal for Numerical Methods in Fluids, 39(9), 821-841.

Grinstein, F. F., Margolin, L. G., & Rider, W. J. (Eds.). (2007). Implicit large eddy simulation: computing turbulent fluid dynamics. Cambridge university press.

Lax, Peter D. Hyperbolic systems of conservation laws and the mathematical theory of shock waves. Vol. 11. SIAM, 1973.

Harten, Amiram, James M. Hyman, Peter D. Lax, and Barbara Keyfitz. “On finite‐difference approximations and entropy conditions for shocks.” Communications on pure and applied mathematics 29, no. 3 (1976): 297-322.

Dukowicz, John K. “A general, non-iterative Riemann solver for Godunov’s method.” Journal of Computational Physics 61, no. 1 (1985): 119-137.

People almost invariably arrive at their beliefs not on the basis of proof but on the basis of what they find attractive.

― Blaise Pascal

When we hear about supercomputing, the media focus, press release is always talking about massive calculations. The bigger is always better with as many zeros as possible with some sort of exotic name for the rate of computation, mega, tera, peta, eta, zeta,… Up and to the right! The implicit proposition is that bigger the calculation, the better the science. This is quite simply complete and utter bullshit. These big calculations providing the media footprint for supercomputing and winning prizes are simply stunts, or more generously technology demonstrations, and not actual science. Scientific computation is a much more involved and thoughtful activity involving lots of different calculations many at a vastly smaller scale. Rarely, if ever, do the massive calculations come as a package including the sorts of evidence science is based upon. Real science has error analysis, uncertainty estimates, and in this sense the massive calculations produce a disservice to computational science by skewing the picture of what science using computers should look like.

This post aims to correct this rather improper vision, and replace it with a discussion of what computational science should be.

With a substantial amount of focus on the drive toward the first exascale supercomputer, it is high time to remind everyone that a single massive calculation is a stunt meant to sell the purchase of said computers, and not science. This week the supercomputing community is meeting in Salt Lake City for a trade show masquerading as a scientific conference. It is simply another in a phalanx of echo chambers we seem to form with increasing regularity across every sector of society. I’m sure the cheerleaders for supercomputing will be crowing about the transformative power of these computers and the boon for science they represent. There will be celebrations of enormous calculations and pronouncements about their scientific value. There is a certain lack of political correctness to the truth about all this; it is mostly pure bullshit.

The entire enterprise pushing toward exascale is primarily a technology push program. It is a furious and futile attempt to stave off the death of Moore’s law. Moore’s law has provided an enormous gain in the power of computers for 50 years and enabled much of the transformative power of computing technology. The key point is that computers and software are just tools; they are incredibly useful tools, but tools nonetheless. Tools allow a human being to extend their own biological capabilities in a myriad of ways. Computers are marvelous at replicating and automating calculations and thought operations at speeds utterly impossible for humans. Everything useful done with these tools is utterly dependent on human beings to devise. My key critique about this approach to computing is the hollowing out of the investigation into devising better ways to use computers and focusing myopically on enhancing the speed of computation.

Truth is only relative to those that ignore hard evidence.

― A.E. Samaan

The core of my assertion that its mostly bullshit comes from looking at the scientific method and its application to these enormous calculations. The scientific method is fundamentally about understanding the World (and using this understanding via engineering). The World is observed either in its natural form, or through experiments devised to unveil difficult to see phenomena. We then produce explanations or theories to describe what we see, and allow us to predict what we haven’t see yet. The degree of comparison between the theory and the observations confirms our degree of understanding. There is always a gap between our theory and our observations, and each is imperfect in its own way. Observations are intrinsically prone to a variety of errors, and theory is always imperfect. The solutions to theoretical models are also imperfect especially when solved via computation. Understanding these imperfections and the nature of the comparisons between theory and observation is essential to a comprehension of the state of our science.

As I’ve stated before, the scientific method applied to scientific computing is embedded in the practice of verification and validation. Simply stated, a single massive calculation cannot be verified or validated (it could be, but not with current computational techniques and the development of such capability is a worthy research endeavor). The uncertainties in the solution and the model cannot be unveiled in a single calculation, and the comparison with observations cannot be put into a quantitative context. The proponents of our current approach to computing want you to believe that massive calculations have intrinsic scientific value. Why? Because they are so big, they have to be the truth. The problem with this thinking is that any single calculation does not contain steps necessary for determining the quality of the calculation, or putting any model comparison in context.

The context of any given calculation is determined by the structure of the errors associated with the computational modeling. For example it is important to understand the nature of any numerical errors, and producing an estimate of these errors. In some (many, most) cases a very good comparison between reality and a model is the result of calibration of uncertain model parameters. In many cases the choices for the modeling parameters are mesh dependent, which produces the uncomfortable outcome where a finer mesh produces a systematically worse comparison. This state of affairs is incredibly common, and generally an unadvertised feature.

An important meta-feature of the computing dialog is the skewing of computer size, design and abilities. For example, the term capability computer comes up where these computers can produce the largest calculations we see, the ones on press releases. These computers are generally the focus of all the attention and cost the most money. The dirty secret is that they are almost completely useless for science and engineering. They are technology demonstrations and little else. They do almost nothing of value to the myriad of programs reporting to use computations to do produce results. All of the utility to actual science and engineering come from the homely cousins of these supercomputers, the capacity computers. These computers are the workhorses of science and engineering because they are set up to do something useful. The capability computers are just show ponies, and perfect exemplars of the modern bullshit based science economy. I’m not OK with this; I’m here to do science and engineering. Are our so-called leaders OK with the focus of attention (and bulk of funding) being non-scientific, media-based, press release generators?

How would we do a better job with science and high performance computing?

The starting point is the full embrace of the scientific method. Taken at face value the observational or experimental community is expected to provide observational uncertainties with their data. These uncertainties should be de-convolved between errors/uncertainties in raw measurement and any variability in the phenomena. Those of us using such measurements for validating codes should demand that observations always come with these uncertainties. By the same token, computational simulations have uncertainties from a variety numerical errors and modeling choices and assumptions that should be demanded. Each of these error sources needs to be characterized to put any comparison with observations/experimental data into context. Without knowledge of these uncertainties on both sides of the scientific process, any comparison is completely untethered.

If nothing else, the uncertainty in any aspect of this process provides a degree of confidence and impact of comparative differences. If a comparison between a model and data is poor, but the data has large uncertainties, the comparison suddenly becomes more palatable. On the other hand small uncertainties with the data would imply that the model is potentially too incorrect. This conclusion would be made once the modeling uncertainty has been explored. One reasonable case would be the identification of large numerical errors in the model’s solution. This is the case where a refined calculation might be genuinely justified. If the bias with a coarse grid is sufficient, a finer grid calculation could be a reasonable way of getting more agreement. There are certainly cases where exascale computing is enabling for model solutions with small enough error to make models useful. This case is rarely made or justified in any massive calculation rather being asserted by authority.

On the other hand numerical error could be a small contributor to the disagreement. In this case, which is incredibly common, a finer mesh does little to rectify model error or uncertainty. The lack of quality comparison is dominated by modeling error, or uncertainty about the parameterization of the models. Worse yet, the models are poor representations of the physics of interest. If the model is a poor representation solving it very accurately is a genuinely wasteful exercise, at least if your goal is scientific in nature. If you’re interested in colorful graphics and a marketing exercise, computer power is your friend, but don’t confuse this with science (or at least good science). The worst case of this issue is a dominant model form error. This is the case where the model is simply wrong, and incapable of reproducing the data. Today many examples exist where models we know are wrong are beat to death with a supercomputer. This does little to advance science, which needs to work at producing a new model that ameliorates the deficiencies in the old model. Unfortunately our supercomputing programs are sapping the vitality from our modeling programs. Even worse, many people seem to confuse computing power as a remedy to model form error.

Equidistributed error is probably the best goal of modeling and simulation that is a balance of numerical and modeling error/uncertainty. This would be the case where the combination of modeling error and uncertainty with a numerical solution has the smallest value. The standard exascale computing driven model would have the numerical error driven to be nearly zero without regard for the modeling error. This ends up being a small numerical error by fiat or proof by authority, proof by overwhelming power. Practically, this is foolhardy and technically indefensible. 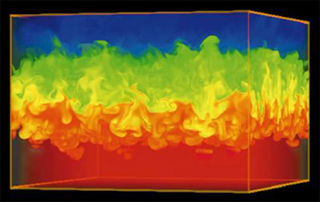The issue is the inability to effectively hunt down modeling uncertainties under these conditions, which is hamstrung by the massive calculations. The most common practice is to assess the modeling uncertainty via some sort of sampling approach. This requires many calculations because of the high-dimensional nature of the problem. Sampling converges very slowly with any mean value for the modeling being proportional to the inverse square root of the number of samples and the measure of the variance of the solution.

Thus a single calculation will have an undefined variance. With a single massive calculation you have no knowledge of the uncertainty either modeling or numerical (at least without have some sort of embedded uncertainty methodology). Without assessing the uncertainty of the calculation you don’t have a scientific or engineering activity. For driving down the inherent uncertainties especially where the modeling uncertainty dominates, you are aided by smaller calculations that can be executed over and over as to drive down the uncertainty. These calculations are always done on capacity computers and never on capability computers. In fact if you try to use a capability computer to do one of these studies, you will be punished and get kicked off. In other words the rules of use enforced via the queuing policies are anti-scientific.

The uncertainty structure can be approached at a high level, but to truly get to the bottom of the issue requires some technical depth. For example numerical error has many potential sources: discretization error (space, time, energy, … whatever we approximate in), linear algebra error, nonlinear solver error, round-off error, solution regularity and smoothness. Many classes of problems are not well posed and admit multiple physically valid solutions. In this case the whole concept of convergence under mesh refinement needs overhauling. Recently the concept of measure-valued (statistical) solutions has entered the fray. These are taxing on computer resources in the same manner as sampling approaches to uncertainty. Each of these sources requires specific and focused approaches to their estimation along with requisite fidelity.

Modeling uncertainty is similarly complex and elaborate. The hardest aspect to evaluate is the form of the physical model. In cases where multiple reasonable models exist, the issue is evaluating the model’s (or sub-model’s) influence on solutions. Models often have adjustable parameters that are unknown or subject to calibration. Most commonly the impact of these parameters and their values are investigated via sampling solutions, an expensive prospect. Similarly there are modeling issues that are purely random, or statistical in nature. The solution to the problem is simply not determinate. Again sampling the solution of a range of parameters that define such randomness is a common approach. All this sampling is very expensive and very difficult to accurately compute. All of our focus on exascale does little to enable good outcomes.

The last area of error is the experimental or observational error and uncertainty. This is important in defining the relative quality of modeling, and the sense and sensibility of using massive computing resources to solve models. We have several standard components in the structure of the error in experiments: the error in measuring a quantity, and then the variation in the actual measured quantity. In one case there is some intrinsic uncertainty in being able to measure something with complete precision. The second part of this is the variation of the actual value in the experiment. Turbulence is the archetype of this sort of phenomena. This uncertainty is intrinsically statistical, and the decomposition is essential to truly understand the nature of the world, and put modeling in proper and useful context.

The bottom line is that science and engineering is evidence. To do things correctly you need to operate on an evidentiary basis. More often than not, high performance computing avoids this key scientific approach. Instead we see the basic decision-making operating via assumption. The assumption is that a bigger, more expensive calculation is always better and always serves the scientific interest. This view is as common as it is naïve. There are many and perhaps most cases where the greatest service of science is many smaller calculations. This hinges upon the overall structure of uncertainty in the simulations and whether it is dominated by approximation error, modeling form or lack of knowledge, and even the observational quality available. These matters are subtle and complex, and we all know that today neither subtle, nor complex sells.

What can be asserted without evidence can also be dismissed without evidence.

― Christopher Hitchens

There is nothing more frightful than ignorance in action.

Our political climate and capability as a nation to engage each other in meaningful, respectful conversations has plummeted to dismal lows. The best description of our 2016 political campaign is a “rolling dumpster fire.” At the core of all of our dysfunction is a critical break from fact-based discussion, confronting objective reality and the ascendency of emotion and spin into the fact-vacuum and alternative reality. One might think that working at a scientific-engineering Laboratory would free me from this appalling trend, but the same dynamic is acutely felt there too. The elements undermining facts and reality in our public life are infesting my work. Many institutions are failing society and contributing to the slow-motion disaster we have seen unfolding. We need to face this issue head-on and rebuild our important institutions and restore our functioning society, democracy and governance.

A big part of the public divorce from facts is the lack of respect and admiration for expertise. Just as the experts and the elite have become suspicious and suspect in the broader public sphere, the same thing has happened in the conduct of science. In many ways the undermining of expertise in science is even worse and more corrosive. Increasingly, there is no tolerance or space for the intrusion of expertise into the conduct of scientific or engineering work. The way this tolerance manifests itself is subtle and poisonous. Expertise is tolerated and welcomed as long as it is confirmatory and positive. Expertise is not allowed to offer strong criticism or the slightest rebuke without regard for the shoddiness of work. If an expert does offer anything that seems critical or negative they can expect to be dismissed and never invited back to provide feedback again. Rather than welcome their service and attention, they are derided as troublemakers and malcontents. We see in every corner of the scientific and technical World a steady intrusion of mediocrity and outright bullshit into our discourse as a result.

Let’s give an example of how this plays out. I’ve seen this happen personally and witnessed it play out via external reviews I observed. I’ve been brought in

to to review technical work for a large important project. The expected outcome was a “rubber stamp” that said the work was excellent, and offered no serious objections. Basically the management wanted me to sign off on the work as being awesome. Instead, I found a number of profound weaknesses in the work, and pointed these out along with some suggested corrective actions. These observations were dismissed and never addressed by the team conducting the work. It became perfectly clear that no such critical feedback was welcome and I wouldn’t be invited back. Worse yet, I was punished for my trouble. I was sent a very clear and unequivocal message, “don’t ever be critical of our work.” 

This personal example of dysfunction is simply the tip of the iceberg for an adversarial attitude toward critical feedback. . We have external review committees visit and treated the same. Most seasoned reviewers know that this is not to be a critical review. It is a light touch and everyone expects to get a glowing report. Any real issues are addressed on the down low and even that is treated with kid gloves. If any reviewer has the audacity to raise an important issue they can expect not to be ever invited back. The end result is the increasingly meaningless nature of any review, and the hollowing out of expertise’s seal of approval. In the process experts and expertise become covered in the bullshit they pedal and become diminished in the end.

This dynamic in review is widespread and fuels the rise of bullshit in public life as well as science and engineering. This propensity to bullshit is driven by a system that cannot deal with conflict or critical feedback. Moreover the system is tilted toward a preconceived result, all is well and no changes are necessary. When this is not the case one is confronted with engaging in conflict against these expectations, or simply getting in line with the bullshit. More and more the bullshit is winning the day. I’ve been personally punished for not towing the line and making a stink. I’ve seen others punished too. It is very clear that failing to provide the desired result bullshit will be punished. The punishments for honesty means that bullshit is on the rise as nothing exists to produce a drive toward quality and results. In the end bullshit is a lot less effort and rewarded a lot more highly.

At the end of the day we can see that the system starts to seriously erode integrity at every level. This is exactly what we are witnessing society-wide. Institutions across the spectrum of public and private life are losing their integrity. Such erosion of integrity in an environment that cannot deal with critical feedback produces a negative loop that feeds upon itself. Bullshit begets more bullshit until the whole thing collapses. We may have just witnessed what the collapse of our political system looks like. We had an election that was almost completely bullshit start to finish. We have elected a completely and utterly incompetent bullshit artist president. Donald Trump was completely unfit to hold office, but he is a consummate con man and bullshit artist. In a sense he is the emblem of the age and the perfect exemplar of our addiction to bullshit over substance.

I personally see myself as a person of substance and integrity. It is increasingly difficult to square who I am with the system I am embedded in. I am not a bullshitter, when I produce bullshit people notice, and I am embarrassed. I am a straight shooter who is committed to progress and excellence. I have a broad set of expertise in science and engineering with a deep desire to contribute to meaningful things. This fundamental nature is increasingly at odds with how the World operates today. I feel a deep drive on the part of the workplace to squash everything positive I stand for. In the place of standing up for my basic nature as a scientific expert, a member of the elite, if you will, I am expected to tow the line and produce bullshit. This bullshit is there to avoid dealing with real issues head on and avoid conflict. The very nature of things stands in opposition to progress and quality, which are threatened by the current milieu.

This gets to the heart of the discussion about what we are losing in this dynamic. We are losing progress society wide. When we allow bullshit to creep into every judgment we make, progress is sacrificed. We bury immediate conflict for long-term decline and plant the seeds for far more deep, widespread and damaging conflict. Such horrible conflict may be unfolding right in front of us in the nature of the political process. By finding our problems and being critical we identify where progress can be made, where work can be done to make the World better. By bullshitting our way through things, the problems persist and fester and progress is sacrificed.

In the current environment where expertise is suspect we see wrong beliefs persist without any real resistance. Falsehoods and myths stand shoulder to shoulder with trust and get treated with equivalence. In this atmosphere the sort of political movements founded completely on absolute bullshit can thrive. Make no mistake, Donald Trump is a master bullshitter, and completely lacks all substance, yet in today’s World he has complete viability. All of us are responsible because we have allowed bullshit to stand on even footing with fact. We have allowed the mechanisms and institutions standing in the way of such bullshit to be weakened and infested with bullshit too. It is time to stand up for truth, integrity and expertise as a shield against this assault against society.

Everything present in the political rise of Donald Trump is playing out in the dynamic at my workplace. It is not as extreme and its presence is subtle, but it is there. We have allowed bullshit to become ubiquitous and accepted. We turn away from calling bullshit out and demanding that real integrity be applied to our work. In the process we implicitly aid and abed the forces in society undermining progress toward a better future. The result of this acceptance of bullshit can be seen in the reduced production of innovation, and breakthrough work, but most acutely in the decay of these institutions.

We have lost the ability to demand difficult decisions to solve seemingly intractable problems. When we do not operate on facts, we can turn away from difficulties and soothe ourselves with falsehoods. Instead of identifying problems and working toward progressive solutions, the problems are minimized and allowed to fester. This is true in the broader public sphere as well as in our scientific environment. I have been actively discouraged from pointing out problems or being critical. The result is stagnation and the steady persistence of problematic states. Instead of working to solve weaknesses, we are urged to accept them or explain them away. This will ultimately yield a catastrophic outcome. At the National level we may have just witnessed such a catastrophe play out in plain view.

In the workplace I feel the key question to ask is “If we don’t look for problems, how can we do important work?” Progress depends on finding weakness and attacking it. This is the principle that I focus on. Confidence comes from being sure you know where to look for problems and up to the challenge of solving them. Empty positivity is a sign of weakness. Yet this is exactly what I am being asked to do at work. The resulting bullshit is a sign of weakness and lack of confidence is being able to constructively solve problems. The need to be positive all the time and avoid criticism is weakness, lack of drive, and lack of conviction in the possibility of progress. We need to refresh out commitment to be constructively critical in the knowledge and belief that we are equal to the task of making the World better. This means stamping out bullshit wherever we see it. There is a lot to do because today we are drowning in it.

With the benefit of time i have a couple projections for the future:

1. The GOP and President Trump will do little or nothing to help the people that voted for them. The key to our democracy is whether they will take any responsibility. If history is our guide they will deflect the blame onto minorities, LBGT, women and
   

   U.S. Republican presidential candidate Donald Trump speaks at a rally in Columbus, Ohio, November 23, 2015. REUTERS/Jay LaPrete – RTX1VIY0

   everyone, but themselves. Will the people fall for the same con as they did when they elected these charlatans?

2. Things will be very dark and dismal for an extended time, and we will spiral toward violence. This may be violence directed by the new ruling class against “enemies of the state”. It also may be violence directed toward the ruling class. Mark my words blood will be shed by Americans at the hands of other Americans.
3. The only way out of this darkness is to work steadfastly to repair our institutions and figure out how to solve our problems in a collective manner for the benefit of all. I work for one of these institutions and we should be taking a long hard look at our role in the great unraveling we are in the midst of.

Facts are stubborn things; and whatever may be our wishes, our inclinations, or the dictates of our passion, they cannot alter the state of facts and evidence.

― John Adams

Footnote: I started writing this on Monday, and like almost everyone I thought the election would turn out differently. It was a genuinely shocking result that makes this topic all the more timely. Instead the results amplified the importance of this entire discussion immensely. The prospect of a President Trump fills me with dread because of the very issues discussed here. Trump exists in an alternative reality and his lack of presence in an objective reality will have real consequences. He is a reality TV star and professional buffoon. He is the most stunningly unqualified person to ever hold that office. I fear what is coming. I also feel the need to be resolved to pick up the pieces from the disaster that will likely unfold. We need to rebuild our institutions and reinstitute a knowledge/facts/reality based governance to guide society forward.

In the past quarter century the role of software in science has made a huge change in importance. I work in a computer research organization that employs many applied mathematicians. One would think that we have a little maelstrom of mathematical thought. Very little actual mathematics takes place with most of them writing software as their prime activity. A great deal of emphasis is placed on software as something to be preserved or invested in. This dynamic places a great deal of other forms of work on the backburner like mathematics (or modeling or algorithmic-methods investigation). The proper question to think about is whether the emphasis on software along with collateral decreases in focus on mathematics or physical modeling is a benefit to the conduct of science.

Doing mathematics should always mean finding patterns and crafting beautiful and meaningful explanations.

― Paul Lockhart

I’ll focus on my wife’s favorite question, “what is code?”(I put this up on a slide when she was in the audience, and she rolled her eyes at me and walked out). If we understand what exactly code is we can answer the question of whether it can be preserved and whether it is worthwhile to do.

The simplest answer to the question at hand is that code is a set of instructions that a computer can understand that provides a recipe provided by humans for conducting some calculations. These instructions could integrate a function, or a differential equations, sort some data out, filter an image, or millions of other things. In every case the instructions are devised by humans to do something, and carried out by a computer with greater automation and speed than humans can possibly manage. Without the guidance of humans, the computer is utterly useless, but with human guidance it is a transformative tool. We see modern society completely reshaped by the computer. Too often the focus of humans is on the tool and not the things that give it power, skillful human instructions devised by creative intellects. Dangerously, science is falling into this trap, and the misunderstanding of the true dynamic may have disastrous consequences for the state of progress. We must keep in mind the nature of computing and man’s key role in its utility.

Mathematics is the cheapest science. Unlike physics or chemistry, it does not require any expensive equipment. All one needs for mathematics is a pencil and paper.

― George Pólya

The manner of treating applied mathematics today serves as an instructive lesson in how out of balance the dynamic is today. Among the sciences mathematics may be the most purely thoughtful endeavor. Some have quipped that mathematics is the most cost efficient discipline, requiring nothing more than time, pen and paper. Often massive progress happens without pen and paper whole the mathematical mind ponders and schemes about theorem, proof and conceptual breakthroughs. Increasingly this idealized model is foreign to mathematicians and the desire for a more concrete product has taken hold. This is most keenly seen in the drive for software as a tangible end product.

Nothing is remotely wrong with creating working software to demonstrate a mathematical concept. Often mathematics is empowered by the tangible demonstration of the utility of the ideas expressed in code. The problem occurs when the code becomes the central activity and mathematics is subdued in priority. Increasingly, the essential aspects of mathematics are absent from the demands of the research being replaced by software. This software is viewed as an investment that must be transferred along to new generations of computers. The issue is that the porting of libraries of mathematical code has become the raison d’etre for research. This porting has swallowed innovation in mathematical ideas whole, and the balance in research is desperately lacking.

Instead of focusing on being mathematicians, we increasingly see software engineering and programming as the focal point for people’s work. Software engineering and maintenance of complex software is a worthy endeavor (more later), but our talented mathematicians should be discovering math, not porting code and finding bugs as their principle professional focus. The discovery of deep, innovative and exciting mathematics promises to provide far more benefit to the future of computing than any software instantiation. New mathematical ideas if focused upon and delivered will ultimately unleash far greater benefits in the long run. This is an obvious thing, yet focus is entirely away from this model. We are steadfastly turning our mathematicians into software engineers.

Let’s get to the crux of the problem with current thinking about software. Mathematical software is like a basic plumbing of lots of codes used for scientific activities, but this model is deeply flawed. It is not like infrastructure at all where the code would be repaired and services after it is built. This leads to the current maintainers of the code to not innovate or extend the intellectual ideas in software, which I would contend is necessary to intellectually own the software. Instead a mathematical body of code is more like an automobile. The auto must be fueled and services, but over time becomes old and outdated needing to be replaced. The classic car has a certain luster and beauty, but its efficiency and utility is far less than a new car. Any automobile can take you places, but eventually the old car cannot compete with the new car. This is how we should think about our mathematical software. It should be serviced and maintained by software professionals, but mathematicians should be working on a new model all the time.

For so much of what we do with computers mathematics forms the core and foundation of the capability. The lack of focus on the actual execution of mathematical research will have long lasting effects on our future. In essence we are living on the mathematical (and physics, engineering, …) research of the past without reinvesting in the next generation of breakthroughs. We are emptying the pipeline of discovery and impoverishing our future. In addition we are failing to take advantage of the skills, talents and imagination of the current generation of scientists. We are creating a deficit of possibility that will harm our future in ways we can scarcely imagine. The guilt lies in the failure of our leaders to have sufficient faith in the power of human thought and innovation to continue to march forward into the future in the manner we have in the
past. People if turned loose on challenging problems will solve them; we always have and past is prolog.

Progress is possible only if we train ourselves to think about programs without thinking of them as pieces of executable code.

― Edsger W. Dijkstra

The key to this notion is putting software in its proper place. Just as a computer itself, software is a tool. Software is an expression of intellect plain and simple. If the intellectual capital isn’t present the value of the software is diminished. Intellectual ownership is a big deal and the key to real value. Increasingly we are creating software where no one working on really owns the knowledge encoded. This is a massively dangerous trend. Unfortunately we are not funding the basic process where the ownership is obtained. Full ownership is established through the creative process, the ability to innovate and create new knowledge grants ownership. Without the creation of new knowledge the intellectual ownership is incomplete. An additional benefit of the ownership is new capability for mankind. The foundation of all of this is mathematical research.

Our foundation is crumbling beneath our feet from abject neglect. Again, like everything else today, the reason for this is a focus on money as the arbitrator of all that is good or bad. We simply do what we are paid to do, no more and no less. No one is paying for math, they are paying for software, it’s as simple as that.

Programs must be written for people to read, and only incidentally for machines to execute.

― Harold Abelson