Rigor alone is paralytic death, but imagination alone is insanity.

― Gregory Bateson

Solving hyperbolic conservation laws provides a rich vein of knowledge to mine and utilize more generally. Most canonically this involves solving the equations of gas dynamics, but the lessons apply to a host of other equations such as magneto-hydrodynamics, multi-material hydrodynamics, oil-water flow, solid mechanics, and on and on. Gas dynamics is commonly visible in the real world, and includes lots of nonlinearity, structure and complexity to contend with. The structures and complexity includes compressible flow structures such as shock waves, rarefactions and contract discontinuities. In more than one dimension you have shear waves, and instabilities that ultimately lead to turbulent flows. With all of these complications to deal with, these flows present numerous challenges to their robust, reliable and accurate simulation. As such, gas dynamics provides a great springboard for robust methods in many fields as well as a proving ground for much of applied math, engineering and physics. It provides a wonderful canvas for the science and art of modeling and simulation to be improved in the vain, but beneficial at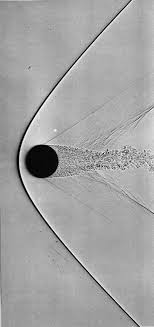tempt at perfection.

Getting a basic working code can come through a variety of ways using some basic methods that provide lots of fundamental functionality. Some of the common options are TVD methods (ala Sweby for example), high order Godunov methods (ala Colella et al), FCT methods (ala Zalesak), or even WENO (Shu and company). For some of these methods the tricks leading to robustness make it into print (Colella, Zalesak come to mind in this regard). All of these will give a passable to even a great solution to most problems, but still all of them can be pushed over the edge with a problem that’s hard enough. So what defines a robust calculation? Let’s say you’ve taken my advice and brutalized your code https://williamjrider.wordpress.com/2017/06/09/brutal-problems-make-for-swift-progress/ and now you need to fix your method https://williamjrider.wordpress.com/2017/06/16/that-brutal-problem-broke-my-code-what-do-i-do/. This post will provide you with a bunch of ideas about techniques, or recipes to get you across that finish line.

You can’t really know what you are made of until you are tested.

― O.R. Melling

The starting basis for getting a robust code is choosing a good starting point, a strong foundation to work from. Each of the methods above would to a significant degree define this. Opinions differ on which of the available options are best, so I won’t be prescriptive about it (I prefer high-order Godunov methods in the interest of transparency). For typical academic problems, this foundation can be drawn from a wide range of available methods, but these methods often are not up to the job in “real” codes. There are a lot more things to add to a method to get you all the way to a production code. These are more than just bells and whistles; the techniques discussed here can be the difference between success and failure. Usually these tricks of the trade are found through hard fought battles and failures. Each failure offers the opportunity to produce something better and avoid problems. The best recipes produce reliable results for the host of problems you ask the code to solve. A great method won’t fall apart when you ask it to do something new either.

The methods discussed above all share some common things. First and foremost is reliance upon a close to bulletproof first order method as the ground state for the higher order method. This is the first step in building robust methods, start with a first-order method that is very reliable and almost guaranteed to give a physically admissible solution. This is easier said than done for general cases. We know that theoretically the lowest dissipation method with all the necessary characteristics is Godunov’s method (see Osher’s work from the mid-1980’s). At the other end of the useful first-order method spectrum is Lax-Friedrichs method, the most dissipative stable method. In a sense these methods give us our bookends. Any method we use as a foundation will be somewhere between these two. Still coming up with a good foundational first-order method is itself an art. The key is choosing a Riemann solver that provides a reliable solution under even pathological circumstances (in lieu of a Riemann solver, a dissipation that is super reliable).

You cannot build a dream on a foundation of sand. To weather the test of storms, it must be cemented in the heart with uncompromising conviction.

― T.F. Hodge

Without further ado let’s get to the techniques that one ought to use. The broadest category of techniques involves adding smart dissipation to methods. This acknowledges that the methods we are using already have a lot of dissipative mechanisms built into them. As a result the added dissipation needs to be selective as hell. The starting point is a careful statement of where the methods already have dissipation. Usually it lies in two distinct places, the most obvious being Riemann solvers or artificial viscosity. The Riemann solver adds an upwind bias to the approximation, which has an implicit dissipative content. The second major source of dissipation is the discretization itself, which can include biases that provide implicit dissipation. For sufficiently complex or nonlinear problems the structural dissipation in the methods are not enough for nonlinear stability. One of the simplest forms for this dissipation is the addition of another dissipative form. For Godunov methods the Lapidus viscosity can be useful because it works at shocks, and adds a multidimensional character. Other viscosity can be added through the Riemann solvers (via so-called entropy fixes, or selecting larger wavespeeds since dissipation is proportional to that). It is important that the dissipation be mechanistically different than the base viscosity, meaning that hyperviscosity (https://williamjrider.wordpress.com/2016/03/24/hyperviscosity-is-a-useful-and-important-computational-tool/) can really be useful to augment dissipation. A general principle is to provide multiple alternative routes to nonlinear stability to support each other effectively.

The building blocks that form the foundation of your great and successful future, are the actions you take today

― Topsy Gift

The second source of dissipation is the fundamental discretization, which implicitly provides it. One of the key aspects of modern discretization are limiters that provide nonlinear stability through effectively adapting the discretization to the solution. These limiters come in various forms, but they all provide the means for the method to choose a favorable discretization for the nature of the solution (https://williamjrider.wordpress.com/2016/06/22/a-path-to-better-limiters/, https://williamjrider.wordpress.com/2016/06/14/an-essential-foundation-for-progress/, https://williamjrider.wordpress.com/2016/06/03/nonlinear-methods-a-key-to-modern-modeling-and-simulation/ ). One of the ways for additional dissipation to enter the method is through a deliberate choice of different limiters. One can bias the adaptive selection of discretization toward more dissipative methods when the solution calls for more care. These choices are important to make when solutions have shock waves, complex nonlinear structures, oscillations, or structural anomalies. For example the minmod limiter based method is the most dissipative second-order, monotonicity-preserving method. It can be used as a less dissipative alternative safety net instead of the first-order methods although its safety is predicated on a bulletproof first order method as a foundation.

Except for all but the most ideal circumstances, the added dissipation is not sufficient to produce a robust method. Very strong nonlinear events that confound classical analysis can still produce problems. All oscillations are very difficult to remove from the solutions and can work to produce distinct threats to the complete stability of the solution. Common ways to deal with these issues in a rather extreme manner are floors and ceilings for various variables. One of the worst things that can happen is a physical quantity moving outside its physically admissible bounds. The simplest example is a density going negative. Density is a positive definite quantity and needs to stay that way for the solution to be physical. It behooves robustness to make sure this does not happen. If it does it is usually catastrophic for the code. This is a simple case and in general quantities should lie within reasonable bounds. Usually when quantities fall outside reasonable bounds the code’s solutions are compromised. It makes sense to explicitly guard against this specifically where a quantity being out of bounds would general a catastrophic effect. For example, sound speeds involve densities and pressure plus a square root operation; a negative value would be disaster.

One can take things a long way toward robustness through using methods that more formally produce bounded approximations. The general case of positivity, or more bounded approximation has been pursued actively. I described the implementation of methods of this sort earlier, (https://williamjrider.wordpress.com/2015/08/06/a-simple-general-purpose-limiter/ ). These methods can go a very long way to giving the robust character one desires, but other means discussed above are still necessary. A large production code with massive meshes and long run times will access huge swaths of phase space and as the physical complexity of problems increases, almost anything that can happen will. It is foolish to assume that bad states will not occur. One also must contend with people using the code in ways the developers never envisioned, and putting the solver into situations where it must survive even when it was designed for them. As a consequence it would be foolish to completely remove the sorts of checks that avert disaster (this could be done, but only with rigorous testing far beyond what most people ever do).

What to concretely do is another question where there are multiple options. One can institute a floating-point trap that locally avoids the possibility of using a negative value for the square root. This can be done in a variety of ways with differing benefits and pitfalls. One simple approach is to take the square root of the absolute value, or one might choose the max of the density and some sort of small floor value. This does little to address the core reason that the approximations produced an unphysical value. There is also little control on the magnitude of the density (the value can be very small), which has rather unpleasant side effects. A better approach would get closer to the root of the problems, which almost without fail comes from the inappropriate application of high-order approximations. One way for this to be applied is to replace the high-order approximations with a physically admissible low-order approximation. This relies upon the guarantees associated with the low-order (first order) approximation as a general safety net for the computational method. The reality is that the first-order method can also go bad, and the floating-point trap may or certainly be necessary even there.

A basic part of the deterministic solution to many problems is the ability to maintain symmetry. The physical world almost invariably breaks symmetry, but it is arguable that numerical solutions to the PDEs should not (I could provide the alternative argument vigorously too). If you want to maintain such symmetry, the code must be carefully designed to do this. A big source of the symmetry breaking is upwind approximations, especially if one choses a bias where zero isn’t carefully and symmetrically treated. One approach is the use of smoothed operators that I discussed at length (https://williamjrider.wordpress.com/2017/03/24/smoothed-operators/, https://williamjrider.wordpress.com/2017/03/29/how-useful-are-smoothed-operators/, https://williamjrider.wordpress.com/2017/04/04/results-using-smoothed-operators-in-actual-code/ ). More generally the use of “if” tests in the code will break symmetry. Another key area for symmetry breaking is the solution of linear systems by methods that are not symmetry preserving. This means numerical linear algebra needs to be carefully approached.

For gas dynamics, the mathematics of the model provide us with some very general character to the problems we solve. Shock waves are the preeminent feature of compressible gas dynamics, and a relatively predominant focal point for methods’ development and developer attention. Shock waves are nonlinear and naturally steepen thus countering dissipative effects. Shocks benefit through their character as garbage collectors, they are dissipative features and as a result destroy information. Some of this destruction limits the damage done by poor choices of numerical treatment. Being nonlinear one has to be careful with shocks. The very worst thing you can do is to add too little dissipation because this will allow the solution to generate unphysical noise or oscillations that are emitted by the shock. These oscillations will then become features of the solution. A lot of the robustness we seek comes from not producing oscillations, which can be best achieved with generous dissipation at shocks. Shocks receive so much attention because their improper treatment is utterly catastrophic, but they are not the only issue; the others are just more subtle and less apparently deadly.

Rarefactions are the benign compatriot to shocks. Rarefactions do not steepen and usually offer modest challenges to computations. Rarefactions produce no dissipation and their spreading nature reduces the magnitude of anything anomalous produced by the simulation. Despite their ease relative to shock waves, the rarefactions do produce some distinct challenges. The simplest case involves centered rarefactions where the characteristic velocity of the rarefaction goes to zero. Since dissipation in methods is proportional to the characteristic velocity, the presence of zero dissipation can trigger disaster and can generate completely unphysical rarefaction shocks (rarefaction shocks can be physical for exotic BZT fluids). More generally for very strong rarefactions one can see small and very worrisome deviations from adhering to the second law, these should be viewed with significant suspicion. The other worrisome feature of most computed rarefactions is the structure of the head of the rarefaction. Usually there is a systematic bump there that is not physical and may produce unphysical solutions for problems featuring very strong expansion waves. This bump actually looks like a shock when viewed through the lens of Lax’s version of the entropy conditions (based on characteristic velocities). This is an unsolved problem at present and represents a challenge to our gas dynamics simulations. The basic issue is that a strong enough rarefaction cannot be solved in an accurate, convergent manner by existing methods.

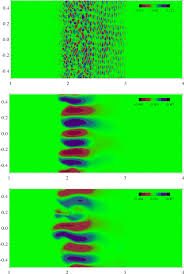
A third outstanding feature of gas dynamics are contact discontinuities, which are classified as linearly degenerate waves. They are quite similar to linear waves meaning that the characteristics do not change across the wave; for the ideal analysis the jumps neither steepen nor spread across the wave. One of the key results is that any numerical error is permanently encoded into the solution. One needs to be careful with dissipation because it never goes away. For this reason people consider steepening the wave to keep it from artificially spreading. It is a bit of an attempt to endow the contact with a little of the character of a shock courting potential catastrophe in the process. This can be dangerous if it is applied to with an interaction with a nonlinear wave, or instability for multidimensional flows. Another feature of the contact is their connection to multi-material interfaces as a material interface can ideally be viewed as a contact. Multi-material flows are a deep well of significant problems and a topic of great depth unto themselves (Abgrall and Karni is an introduction which barely scratches the surface!).

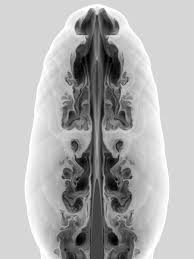
The fourth standard feature is shear waves, which are a different form of linearly degenerate waves. Shear waves are heavily related to turbulence, thus being a huge source of terror. In one dimension shear is rather innocuous being just another contact, but in two or three dimensions our current knowledge and technical capabilities are quickly overwhelmed. Once you have a turbulent flow, one must deal with the conflation of numerical error, and modeling becomes a pernicious aspect of a calculation. In multiple dimensions the shear is almost invariably unstable and solutions become chaotic and boundless in terms of complexity. This boundless complexity means that solutions are significantly mesh dependent, and demonstrably non-convergent in a point wise sense. There may be a convergence in a measure-valued sense, but these concepts are far from well defined, fully explored and technically agreed upon.

A couple of general tips for developing a code involves the choice of solution variables. All most without fail, the worst thing you can do is define the approximations using the conserved quantities. This is almost always a more fragile and error prone manner to compute solutions. In general the best approach is to use the so-called primitive variables (https://williamjrider.wordpress.com/2016/08/08/the-benefits-of-using-primitive-variables/ ). The variables are clear in their physical implications and can be well-bounded using rational means. Using primitive variables is better for almost anything you want to do. The second piece of advice is to use characteristic variables to as great an extent as possible. This always implies some sort of one-dimensional thought. Despite this limitation, the benefits of characteristic variables are so extreme as to justify their use even under these limited circumstances.

A really good general rule is to produce thermodyanically consistent solutions. In other words, don’t mess with thermodynamic consistency, and particularly with the second law of thermodynamics. Parts of this thermodynamic consistency are the dissipative nature of physical solutions and the active adherence to entropy conditions. There are several nuances to this adherence that are worth discussing in more depth. It is generally and commonly known that shocks increase entropy. What isn’t so widely appreciated is the nature of this increase being finite and adheres to a scaling that is proportional to the size of the jump. The dissipation does not converge toward zero, but rather toward a finite value related to the structure of the solution.

The second issue is dissipation free nature of the rest of the flow especially rarefactions. The usual aim of solvers is to completely remove dissipation, but that runs the risk of violating the second law. It may be more advisable to keep a small positive dissipation working (perhaps using a hyperviscosity partially because control volumes add a nonlinear anti-dissipative error). This way the code stays away from circumstances that violate this essential physical law. We can work with other forms of entropy satisfaction too. Most notably is Lax’s condition that identifies the structures in a flow by the local behavior of the relevant characteristics of the flow. Across a shock the characteristics flow into the shock, and this condition should be met with dissipation. These structures are commonly present in the head of rarefactions.

One of the big things that can be done to improve solutions is the systematic use of high-order approximations within methods. These high-order elements often involve formal accuracy that is much higher than the overall accuracy of the methods. For example a fourth-order approximation to the first derivative can be used to great effect with a method that only provides an overall second-order accuracy. With methods like PPM and FCT this can be taken to greater extremes. There one might use a fifth or sixth-order approximation for edge values even though the overall method is third order in one dimension or second-order in two or three dimensions. Another aspect of high order accuracy is better accuracy at local extrema. A usual approach to limiting to provide nonlinear stability clips extrema and computes them at first-order accuracy. In moving to limiters that do not clip extrema so harshly, excessive care must be taken so that the resulting method is not fragile and prone to oscillations. Alternatively, extrema-preserving methods can be developed that are relatively dissipative even compared to the better extrema clipping methods. Weighted ENO methods of almost any stripe are examples where the lack of extrema clipping is purchased at the cost of significant dissipation and relatively low overall computational fidelity. A better overall approach would be to use methods I have devised or the MP methods of Suresh and Huynh. Both of these methods are significantly more accurate than WENO methods.

One of the key points of this work is to make codes robust. Usually these techniques are originally devised as “kludges” that are crude and poorly justified. They have the virtue of working. The overall development effort is to guide these kludges into genuinely defensible methods, and then ultimately to algorithms. One threads the needle between robust solutions and technical rigor that lends confidence and faith in the simulation. The first rule is get an answer, then get a reasonable answer, then get an admissible answer, and then get an accurate answer. The challenges come through the systematic endeavor to solve problems of ever increasing difficulty and expand the capacity of simulations to address an ever-broader scope. We then balance this effort with the availability of knowledge to support the desired rigor. Our standards are arrived at philosophically through what constitutes an acceptable solution to our modeling problems.

Consistency and accuracy instills believability

― Bernard Kelvin Clive

Sweby, Peter K. “High resolution schemes using flux limiters for hyperbolic conservation laws.” SIAM journal on numerical analysis 21, no. 5 (1984): 995-1011.

Jiang, Guang-Shan, and Chi-Wang Shu. “Efficient implementation of weighted ENO schemes.” Journal of computational physics 126, no. 1 (1996): 202-228.

Colella, Phillip, and Paul R. Woodward. “The piecewise parabolic method (PPM) for gas-dynamical simulations.” Journal of computational physics 54, no. 1 (1984): 174-201.

Colella, Phillip. “A direct Eulerian MUSCL scheme for gas dynamics.” SIAM Journal on Scientific and Statistical Computing 6, no. 1 (1985): 104-117.

Bell, John B., Phillip Colella, and John A. Trangenstein. “Higher order Godunov methods for general systems of hyperbolic conservation laws.” Journal of Computational Physics 82, no. 2 (1989): 362-397.

Zalesak, Steven T. “Fully multidimensional flux-corrected transport algorithms for fluids.” Journal of computational physics 31, no. 3 (1979): 335-362.

Zalesak, Steven T. “The design of Flux-Corrected Transport (FCT) algorithms for structured grids.” In Flux-Corrected Transport, pp. 23-65. Springer Netherlands, 2012.

Quirk, James J. “A contribution to the great Riemann solver debate.” International Journal for Numerical Methods in Fluids 18, no. 6 (1994): 555-574.

Woodward, Paul, and Phillip Colella. “The numerical simulation of two-dimensional fluid flow with strong shocks.” Journal of computational physics 54, no. 1 (1984): 115-173.

Abgrall, Rémi, and Smadar Karni. “Computations of compressible multifluids.” Journal of computational physics 169, no. 2 (2001): 594-623.

Osher, Stanley. “Riemann solvers, the entropy condition, and difference.” SIAM Journal on Numerical Analysis 21, no. 2 (1984): 217-235.

Suresh, A., and H. T. Huynh. “Accurate monotonicity-preserving schemes with Runge–Kutta time stepping.” Journal of Computational Physics 136, no. 1 (1997): 83-99.

Rider, William J., Jeffrey A. Greenough, and James R. Kamm. “Accurate monotonicity-and extrema-preserving methods through adaptive nonlinear hybridizations.” Journal of Computational Physics 225, no. 2 (2007): 1827-1848.

 

 

The mystery of human existence lies not in just staying alive, but in finding something to live for.

― Fyodor Dostoyevsky

There is little doubt that we are living through monumental times in the history of humanity. I was born the child of the Cold War seeing that conflict end as I transitioned to adulthood and my professional life then seeing the birth of globalism powered by technology and communication unthinkable a generation before. My chosen profession looks increasingly like a relic of that Cold War, and increasingly irrelevant to the World that unfolds before me. My workplace is failing to keep pace with change, and I’m seeing it fall behind modernity in almost every respect. It’s a safe, secure job, but lacks most of the edge the real World offers. All of the forces unleashed in today’s World make for incredible excitement, possibility, incredible terror and discomfort. The potential for humanity is phenomenal, and the risks are profound. In short, we live in simultaneously in incredibly exciting and massively sucky times. Yes, both of these seemingly conflicting things can be true.

We are seeing a massive collision of the past and future across the globe pitting the forces of stability and progress against each other. We see the political power of conservative, anti-progress forces gaining the upper hand recently. The resurgent right wing seeks to push back against the changes pushed by demographics and empowered by technology. The reinvigorated tendency to use bigotry, hate and violence increasingly in a state-sponsored way is increasing. The violence against change is growing whether it is by governments or terrorists. What isn’t commonly appreciated is the alliance in violence of the right wing and terrorists. Both are fighting against the sorts of changes modernity is bringing. The fight against terror is giving the violent right wing more power. The right wing and Islamic terrorists have the same aim, undoing the push toward progress with modern views of race, religion and morality. The only difference is the name of the prophet the violence is done in name of.

This unholy alliance draws its power from the bookends of society. On one hand you have the poorer, uneducated masses of the population, and on the other you have the entrenched interests of the rich and powerful. The poor and uneducated are not able to manage the changes in society and want the brakes put on progress. The rich and powerful like the status quo and fear progress because it might not favor them as well. Together they ally against the middle class, who stands to benefit the most from progress. The alliance empowers violence among the poor, grows their ranks through polices that favor the wealthy. We see this happening across the globe where right wing, racist, Nationalist, overtly religious movements are attacking any societal progress. The rich and powerful pull the strings for their own purposes, enhancing their power and wealth at the expense of society as a whole.

The most insidious force of this unhealthy alliance is terrorism. The right wing wants to fight terrorism through enhancing the police-National-security state, which provides the rich and powerful the tools to control their societies as well. They also wage war against the sources of terrorism creating the conditions and recruiting for more terrorists. The police states have reduced freedom and lots of censorship, imprisonment, and opposition to personal empowerment. The same police states are effective at repressing minority groups within nations using the weapons gained to fight terror. Together these all help the cause of the right wing in blunting progress. The two allies like to kill each other too, but the forces of hate; fear and doubt work to their greater ends. In fighting terrorism we are giving them exactly what they want, the reduction of our freedom and progress. This is also the aim of right wing; stop the frightening future from arriving through the imposition of traditional values. This is exactly what the religious extremists want be they Islamic or Christian.

Driving the conservatives to such heights of violence and fear are changes to society of massive scale. Demographics are driving the changes with people of color becoming impossible to ignore, along with an aging population. Sexual freedom has emboldened people to break free of traditional boundaries of behavior, gender and relationships. Technology is accelerating the change and empowering people in amazing ways. All of this terrifies many people and provides extremists with the sort of alarmist rhetoric needed to grab power. We see these forces rushing headlong toward each other with society-wide conflict the impact. Progressive and conservative blocks are headed toward a massive fight. This also lines up along urban and rural lines, young and old, educated and uneducated. The future hangs in the balance and it is not clear who has the advantage.

The purpose of life is to contribute in some way to making things better.

― Robert F. Kennedy

The cell phone becoming a platform for communication and commerce at a scale unimaginable a decade ago has transformed the economics of the World. People are now connected globally through the cell phone, and these mini-computers allow new models of economic activity to sprout up constantly. The changes to how we live are incalculable with the cell phone shaping both our social and economic structures in deep and unforeseen ways. The social order is being shaped by the ability to connect to people in deeply personal ways without the necessity of proximity. We meet people online now and form relationships without ever meeting physically. Often people have had ongoing relationships with people they’ve never met or met rarely. They can maintain communication via text, audio or video with amazing ease. This starts to form different communities and relationships that are shaking culture. It’s mostly a middle class phenomenon and thus the poor are left out, and afraid.

The way we live, work, sleep, eat, and relate to each other has transformed completely in a decade. The balance of personal empowerment and threat to privacy sits at the precipice. The cell phone has made the Internet personal and ubiquitous redefining our social order. This excites people like me, and scares the shit out of others. We are seeing a change in our society at a pace unseen in the course of history. Violence is a likely result of the pace and intensity of this change. Economic displacements are accelerating, and our standard systems are poor at coping with everything. Everything from schools too many employers are incapable of evolving fast enough to benefit from the change. I perfect example are institutions like I work for. Despite being high tech and full of educated people, it is conservative, rule following, compliant, security conscious (too a paranoid level) and obsessively bureaucratic, largely incapable of adopting technology or taking risks with anything. My level of frustration is growing with each passing day. I’m seeing modernity pull ahead of me in the workplace due to fear and incompetence.

For example in my public life, I am not willing to give up the progress, and feel that the right wing is agitating to push the clock back. The right wing feels the changes are immoral and frightening and want to take freedom away. They will do it in the name of fighting terrorism while clutching the mantle of white nationalism and the Bible in the other hand. Similar mixes are present in Europe, Russia, and remarkably across the Arab world. My work World is increasingly allied with the forces against progress. I see a deep break in the not to distant future where the progress scientific research depends upon will be utterly incongruent with the values of my security-obsessed work place. The two things cannot live together effectively and ultimately the work will be undone by its inability to commit itself to being part of the modern World. The forces of progress are powerful and seemingly unstoppable too. We are seeing the unstoppable force of progress meet the immovable object of fear and oppression. It is going to be violent and sudden. My belief in progress is steadfast, and unwavering. Nonetheless, we have had episodes in human history where progress was stopped. Anyone heard of the dark ages? It can happen.

We’ll be remembered more for what we destroy than what we create.

― Chuck Palahniuk

I’ve been trying to come to grips with the changes in where I work. My workplace is adapting too slowing to modern life, and the meaning in work has become difficult to square with realities. The sense that my work doesn’t matter anymore has become increasingly palpable. I’ve gone from working for a clear sense of purpose and importance to a job that increasingly seethes with irrelevance. Every action from my masters communicates the lack of value of my work. Creating a productive and efficient workplace is never-ever important. We increasingly have no sense of importance in our work. This is delivered with disempowering edicts and policies that conspire to shackle me, and keep me from doing anything. The real message is that nothing you do is important enough to risk fucking up. I’m convinced that the things making work suck are strongly connected to everything else.

With each passing day the nature and forces at work and the rest of my life become more separate. It becomes hard to feel like I’m making the best, most productive use of my time and effort in work when I know so much effective productive effort is being left behind. The motives and rules of my employer are focused on safety and security above all else. Everything that makes modern life tick makes them uncomfortable. In addition things are evolving so fast for technology that organizations like mine cannot keep up. I can adapt quickly and learn, but if I do my desires and knowledge will become a source of tension rather than an advantage. If I keep up with technology I am more likely to be frustrated than productive. This is already happening and it is driving me up the wall.

The problem many organizations (companies, universities, Laboratories) are that they are large and move slowly. With a pace of change that is large by any historical standard, they don’t keep up or adapt. You get into a position where the organization is falling behind, and the forces of fear and hesitation are deadly. Add in a government who supplies the funding with rules galore and strings attached and you have the recipe for falling behind. Unless the organization, its leadership, and its people commit to adapting and pushing themselves forward, the organization will stagnate or be left behind by the exciting innovations shaping the World today. When the motivation of the organization fails to emphasize productivity and efficiency, the recipe is disastrous. Modern technology offers the potential for incredible advances, but only if they’re seeking advantage. If minds are not open to making things better, it is a recipe for frustration.

This ends up being a microcosm of today’s World. Modern advances in technology or society offer tremendous advantages for those willing to be bold, but they come with risk and discomfort. Many are deeply tied to the past and the old way of doing things along with old-fashioned sense of purpose. There is an inability or unwillingness to accept the potential of the modern. Without bold and willing endeavor, the new World passes organization by. This is where I feel the greatest pain, the passive manner in which the modern World passes my organization by. It is not unlike the broader social themes of those who accept the modern World, and the conservative resistance to everything. Organizations who fail to embrace the potential of the modern world unwittingly enter into the opposition to change, and assist the conservative attempt to hold onto the past.

The question to ask is whether these organization whose history and greatness are grounded in a time gone by can evolve into something modern. Do these organizations even want to change? Can they make the change even if they want to while tethered to the past? For those of us who are part of publically focused organizations, we are caught in between the forces raging politically. The institutions of government will almost certainly resist and avoid change. The result will be a slow decline and almost certain death for these organizations as the World changes. The alternative is the World not changing and progress stopping, this outcome is certainly worse for humanity.

History is always written by the winners. When two cultures clash, the loser is obliterated, and the winner writes the history books-books which glorify their own cause and disparage the conquered foe. As Napoleon once said, ‘What is history, but a fable agreed upon?

― Dan Brown

 

The possession of knowledge does not kill the sense of wonder and mystery. There is always more mystery.

― Anaïs Nin

Let’s say you’ve completely bought into my advice and decide to test the hell out of your code. You found some really good problems that “go to eleven.” If you do things right, your code will eventually “break” in some way. The closer you look, the more likely it’ll be broken. Heck your code is probably already broken, and you just don’t know it! Once it’s broken, what should you do? How do you get the code back into working order? What can you do to figure out why it’s broken? How do you live with the knowledge of the limitations of the code? Those limitations are there, but usually you don’t know them very well. Essentially you’ve gone about the process of turning over rocks with your code until you find something awfully dirty-creepy crawly underneath. You then have mystery to solve, and/or ambiguity to live with from the results.

An expert is someone who knows some of the worst mistakes that can be made in his subject, and how to avoid them.

― Werner Heisenberg

I’ll deal with the last question first, how to live with the knowledge of limitations. This is a sort of advice to grow up, and be an adult about things. Any method or code is going to be limited in what it can do. Some of these limitations are imposed by theory, or by practicality, or expense, some of the limitations simply get at the limits of our knowledge and technology today. One of the keys to being an expert in a given field is a deep

understanding of what can and cannot be done, and why. What better way of becoming an expert than purposefully making “mistakes?” Do you understand what the state of the art is? Do you know what is challenging to the state of the art? What are the limits imposed by theory? What do other people do to solve problems and what are the pros and cons to their approach? Exploring these questions, and stepping well outside the confines of comfort provided by success drive a deep knowledge of all of these considerations. When properly applied the art of testing codes delves into a deep knowledge of failures as the fuel for learning and the acquisition of knowledge.

So how might you see your code break? In the worst case the problem might induce an outright instability and the code will blow up. Sometimes the blow up will happen through the production of wild solutions, or even violations of the floating number limits of the computer (NaN’s or not a number will appear in output). Other problems look like corrupted data where the solution doesn’t blow up, but the solution is clearly very wrong. Moving down the chain of bad things we might simply see solutions outside the bounds of what is reasonable or admissible for valid solutions. As we walk through this gallery of bad things each succeeding step is subtler than the last. In our approach to breakage, an analytical solution to a problem can prove invaluable because it provides an unambiguous standard for the solution that can be as accurate as you please.

Next, we simply see solutions that are oscillatory or wiggly. These wiggles can go all the way from dangerous to cosmetic in their character. Sometimes the wiggles might interact with genuinely physical features in a model, and the imperfection is a real modeling problem. Next, we get into the real weeds of solution problems, and start to see failures that can go unnoticed without expert attention. One of the key things is the loss of accuracy in a solution. This could be the numerical level of error being wrong, or the rate of convergence of the solution being outside the theoretical guarantees for the method (convergence rates are a function of the method and the nature of the solution itself). Sometimes this character is associated with an overly dissipative solution where numerical dissipation is too large to be tolerated. At this subtle level we are judging failure by a high standard based on knowledge and expectations driven by deep theoretical understanding. These failings generally indicate you are at a good level of testing and quality.

Once the code is broken in some way, it is time to find out why. The obvious breakage where the solution simply falls apart is the best case to deal with because the failings are so obvious. The first thing you should always do is confirm that you’re solving the problem you think you are, and you’re solving it the way you think you are. This involves examining your input and control of the code to make certain that everything is what you expect it to be. Once you’re sure about this important detail, you can move to the sleuthing. For the obvious code breakdowns you might want to examine how the solution starts to fall apart as early in the process as you can. Is the problem localized near a boundary or a certain feature? Does it happen suddenly? Is there a slow, steady build up toward disaster? The answers all point at different sources for the problem. They tell how and where to look.

One of the key things to understand with any failure is the stability of the code and its methods. You should be intimately familiar with the conditions for stability for the code’s methods. You should assure that the stability conditions are not being exceeded. If a stability condition is missed, or calculated incorrectly, the impact is usually immediate and catastrophic. One way to do this on the cheap is modify the code’s stability condition to a more conservative version usually with a smaller safety factor. If the catastrophic behavior goes away then it points a finger at the stability condition with some certainty. Either the method is wrong, or not coded correctly, or you don’t really understand the stability condition properly. It is important to figure out which of these possibilities you’re subject to. Sometimes this needs to be studied using analytical techniques to examine the stability theoretically.

One of the key things to understand extremely well is the state of the art in a given field. Are there codes and methods that can solve the problem well or without problems? Nothing can replace an excellent working knowledge of what experts in the field are doing. The fastest way to solve a problem is understand and potentially adopt what the best and brightest are already doing. You also have a leg up on understanding what the limits of knowledge and technology are today, and whether you’ve kept up to the boundary of what we know. Maybe it is research to make you code functional, and if you fix it, you might have something publishable! If so, what do they do differently than your code? Can you modify how your code runs to replicate their techniques? If you can do this and reproduce the results that other are getting then you have a blueprint on how to fix your code.

Another approach to take is systematically make the problem you’re solving easier until the results are “correct,” or the catastrophic behavior is replaced with something less odious. An important part of this process is more deeply understand how the problems are being triggered in the code. What sort of condition is being exceeded and how are the methods in the code going south? Is there something explicit that can be done to change the methodology so that this doesn’t happen? Ultimately, the issue is a systematic understanding of how the code and its method’s behave, their strengths and weaknesses. Once the weakness is exposed in the testing can you do something to get rid of it? Whether the weakness is a bug or feature of the code is another question to answer. Through the process of successively harder problems one can make the code better and better until you’re at the limits of knowledge.

The foundation of data gathering is built on asking questions. Never limit the number of hows, whats, wheres, whens, whys and whos, as you are conducting an investigation. A good researcher knows that there will always be more questions than answers.

― Karl Pippart III

Whether you are at the limits of knowledge takes a good deal of experience and study. You need to know the field and your competition quite well. You need to be willing to borrow from others and consider their success carefully. There is little time for pride, if you want to get to the frontier of capability; you need to be brutal and focused along the path. You need to keep pushing your code with harder testing and not be satisfied with the quality. Eventually you will get to problems that cannot be overcome with what people know how to do. At that point your methodology probably needs to evolve a bit. This is really hard work, and prone to risk and failure. For this reason most codes never get to this level of endeavor, its simply too hard on the code developers, and worse on those managing them. Today’s management of science simply doesn’t enable the level of risk and failure necessary to get to the summit of our knowledge. Management wants sure results and cannot deal with ambiguity at all, and striving at the frontier of knowledge is full of it, and usually ends up failing.

The most beautiful experience we can have is the mysterious. It is the fundamental emotion that stands at the cradle of true art and true science.

― Albert Einstein

At the point you meet the frontier, it is time to be willing to experiment with your code (experimentation is great to do even safely within the boundaries of know how). Often the only path forward is changing the way you solve problems. One key is to not undo all the good things you can already do in the process. Quite often one might actually solve the hard problem is some way (like a kludge), only to find out that things that used to be correct and routine for easier problems have been wrecked in the process. That is a back to the drawing board moment! For the very hard problem you may simply be seeking robustness and stability (running the problem to completion), and the measures taken to achieve this do real damage to your bread and butter. You need to be prepared to instrument and study your output in new ways. You are now an explorer, and innovator. Sometimes you need to tackle the problem from a different perspective, challenge your underlying beliefs and philosophies.

The true measure of success is how many times you can bounce back from failure.

― Stephen Richards

At this point its useful to point out that the literature is really bad at documenting what we don’t know. Quite often you are rediscovering something lots of experts already know, but can’t publish. This is one of the worst things about the publishing of research, we really only publish success, and not failure. As a result we have a very poor idea of what we can’t do. It’s only available through inference. Occasionally the state of what can’t be done is published, but usually not. What you may not realize that you are crafting a lens on the problem and a perspective that will shape how you try to solve it. This process is a wonderful learning opportunity and the essence of research. For all these reasons it is very hard and almost entirely unsupportable.

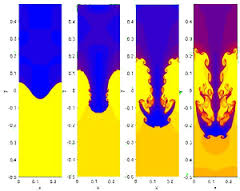Another big issue is finding general purpose fixes for hard problems. Often the fix to a really difficult problem wrecks your ability to solve lots of other problems. Tailoring the solution to treat the difficulty and not destroy the ability to solve other easier problems is an art and the core of the difficulty in advancing the state of the art. The skill to do this requires fairly deep theoretical knowledge of a field study, along with exquisite understanding of the root of difficulties. The difficulty people don’t talk about is the willingness to attack the edge of knowledge and explicitly admit the limitations of what is currently done. This is an admission of weakness that our system doesn’t support. When fixes aren’t general purpose, one clear sign is a narrow range of applicability. If its not general purpose and makes a mess of existing methodology, you probably don’t really understand what’s going on.

Let’s get to a general theme in fixing problems, add some dissipation to stabilize things and get rid of worrisome features. In the process you often end up destroying the very features of the solution you most want to produce. The key is to identify the bad stuff and keep the good stuff, and this comes from a deep understanding plus some vigorous testing. Dissipation almost always results in a more robust code, but the dissipation needs to be selective, or the solution is arrived at in a wasteful manner. As one goes even deeper into the use of dissipation, the adherence to the second law of thermodynamics rears its head, and defines a tool of immense power if wielded appropriately. A key is to use deep principles to achieve a balanced perspective on dissipation where it is used appropriately in clearly defensible, but limited ways. Even today applying dissipation is still an art, and we struggle to bring more science and principle to its application.

I’ve presented a personally biased view of how to engage in this sort of work. I’m sure other fields will have similar, but different rules for engaging in fixing codes. The important thing is putting simulation codes to the sternest tests they can take, exposing their weaknesses and repairing them. One wants to continually do this until you hit the proverbial wall of our knowledge and ability. Along the way you create a better code, learn the field of endeavor and grow the knowledge and capability of yourself. Eventually the endeavor leads to research and the ability to push the field ahead. This is also the way of creating experts, and masters of a given field. People move from simply being competent practitioners to masters and leaders. This is an unabashed good for everyone, and not nearly encouraged enough. It definitely paves the way forward and produces exceptional results.

A pessimist sees the difficulty in every opportunity; an optimist sees the opportunity in every difficulty.

― Winston S. Churchill

 

or the alternative title “These Problems go to Eleven!”

Fortunate are those who take the first steps.

― Paulo Coelho

When thinking about problems to run with a computer code there is both a fun and a harsh way to think about them. I’ll start with the fun way, borrowing from the brilliant movie “This is Spinal Tap” and the hilarious interview with the lead guitarist from the band,

Nigel Tufnel: The numbers all go to eleven. Look, right across the board, eleven, eleven, eleven and…

Marty DiBergi: Oh, I see. And most amps go up to ten?

Nigel Tufnel: Exactly.

Marty DiBergi: Does that mean it’s louder? Is it any louder?

Nigel Tufnel: Well, it’s one louder, isn’t it? It’s not ten. You see, most blokes, you know, will be playing at ten. You’re on ten here, all the way up, all the way up, all the way up, you’re on ten on your guitar. Where can you go from there? Where?

Marty DiBergi: I don’t know.

Nigel Tufnel: Nowhere. Exactly. What we do is, if we need that extra push over the cliff, you know what we do?

Marty DiBergi: Put it up to eleven.

Nigel Tufnel: Eleven. Exactly. One louder.

Marty DiBergi: Why don’t you make ten a little louder, make that the top number and make that a little louder?

Nigel Tufnel: [pauses] These go to eleven.

To make the best progress we need to look for problems that “go to eleven.” Even if the difficulty is somewhat artificial, the best problems are willfully extreme, if not genuinely silly. They expose the mechanisms that break methods. Often these problems are simplified versions of what we know brings the code to its knees, and serve as good blueprints for removing these issues from the code’s methods. Alternatively, they provide proof that certain pathological behaviors do or don’t exist in a code. Really brutal problems that “go to eleven” aid the development of methods by highlighting where improvement is needed clearly. Usually the simpler and cleaner problems are better because more codes and methods can run them, analysis is easier and we can successfully experiment with remedial measures. This allows more experimentation and attempts to solve it using diverse approaches. This can energize rapid progress and deeper understanding.

The greater the obstacle, the more glory in overcoming it.

― Molière

I am a deep believer in the power of brutality at least when it comes to simulation codes. I am a deep believer that we are generally too easy on our computer codes; we should endeavor to break them early and often. A method or code is never “good enough”. The best way to break our codes is attempt to solve really hard problems that are beyond our ability to solve today. Once the solution of these brutal problems is well enough in hand, one should find a way of making the problem a little bit harder. The testing should actually be more extreme and difficult than anything we need to do with codes. One should always be working at, or beyond the edge of what can be done instead of safely staying within our capabilities. Today we are too prone to simply solving problems that are well in hand instead of pushing ourselves into the unknown. This tendency is harming progress.

Stark truth, is seldom met with open arms.

― Justin K. McFarlane Beau

Easy problems make codes look good because they don’t push the boundaries. Easy problems are important for checking the code’s ability to be correct and work when everything is going right. The codes need to continue working when everything is going wrong too. A robust code is functional under the worst of circumstances one might encounter. The brutal problems are good at exposing many of the conditions where things go wrong, and pushing the codes to be genuinely robust. These conditions almost invariably appear in real problems, and good codes can navigate the difficulties without falling apart. Over time good codes can go from falling apart to solving these brutal problems accurately. When this happens we need to come up with new problems to brutalize the codes. We should always be working on the edge or over the edge of what is possible; safe and sound is no way to make things better.

Happiness is not the absence of problems; it’s the ability to deal with them.

― Steve Maraboli

The use of brutal problems has helped drive codes forward for decades. A long time ago simple problems that we routinely solve today brought codes to their collective knees. Examples of such problems for shock physics codes are the Sedov-Taylor blast wave and Noh’s problem. Scientists came up with new ways to solve problems that brought these problems to heel. Rather than rest upon our laurels, we found new problems to bring the codes down. We still solve the older, now tamed brutal problems, but now they are easy. Once we slay one dragon, it is time to construct a bigger, more dangerous dragon to do battle with. We should always test our mettle against a worthy opponent rather than matching up with a patsy. Getting fabulous results on a super-easy problem looks great, but does little or nothing to improve us. Through this process we progress and our codes get better and better. This is how we challenge ourselves systematically always working with the premise that we can improve and get better. Brutal problems provide a concrete focus for improvement.

A challenge only becomes an obstacle when you bow to it.

― Ray A. Davis

What does this process look like concretely? We have problems that used to push the boundaries of our ability such as the Sod shock tube. It used to be a problem we couldn’t solve well. Shock tube problems have the added benefit of having exact solutions (Noh and Sedov-Taylor do too), so agreement and error have little to no ambiguity. Solutions either had oscillations or they were inaccurate and very heavily diffused. Often important features in the solution were seriously corrupted. This problem appeared in the literature at a seminal time in the development of numerical methods for shock physics and offered a standard way of testing and presenting results.

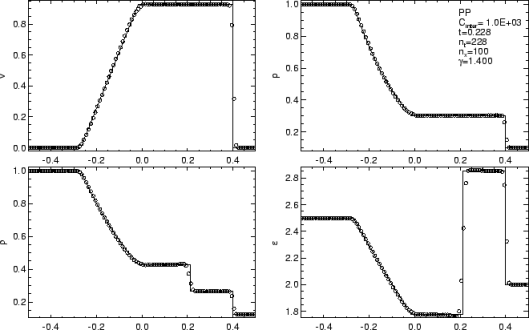By the time a decade had passed after the introduction of Sod’s problem almost all of the pathological solutions we used to see had disappeared and far better methods existed (not because of Sod’s problem per se, but something was “in the air” too). The existence of a common problem to test and present results was a vehicle for the community to use in this endeavor. Today, the Sod problem is simply a “hello World” for shock physics and offers no real challenge to a serious method or code. It is difficult to distinguish between very good and OK solutions with results. Being able to solve the Sod problem doesn’t really qualify you to attack really hard problems either. It is a fine opening ante, but never the final call. The only problem with using the Sod problem today is that too many methods and codes stop their testing there and never move to the problems that challenge our knowledge and capability today. A key to making progress is to find problems where things don’t work so well, focus attention on changing that.

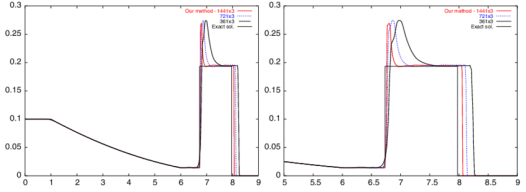Therefore, if we want problems to spur progress and shed light on what works, we need harder problems. For example, we could systematically up the magnitude of the variation in initial conditions in shock tube problems until results start to show issues. This usefully produces harder problems, but really hasn’t been done (note to self this is a really good idea). One problem that produces this comes from the National Lab community in the form of LeBlanc’s shock tube, or its more colorful colloquial name, “the shock tube from Hell.” This is a much less forgiving problem than Sod’s shock tube, and that is an understatement. Rather than jumps in pressure and density of about one order of magnitude, the jump in density is 1000-to-1 and the jump in pressure is one billion-to-one. This stresses methods far more than Sod and many simple methods can completely fail. Most industrial or production quality methods can actually solve the problem albeit with much more resolution than Sod’s problem requires (I’ve gotten decent results on Sod’s problem on mesh sequences of 4-8-16 cells!). For the most part we can solve LeBlanc’s problem capably today, so its time to look for fresh challenges.

One such challenge is posed by problems with void in them, or those that dynamically produce vacuum conditions. We have found that this class of problems simply is not solved effectively with current methods. Every method I’ve looked at fails in some way shape or form. None of them converge to the correct solution once the problem gets close enough to vacuum or void conditions. The only methods that appear to work at all explicitly track the position of the vacuum, so my statement of dysfunction should be applied to shock capturing methods. It does not seem to be a well-appreciated or well-studied problem thus may be ripe for the picking. Running this problem and focusing on results would provide impetus for improving this clearly poor state of affairs.

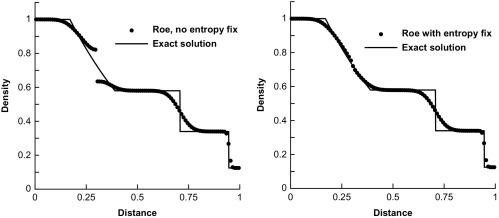Other good problems are devised though knowing what goes wrong in practical calculation. Often those who know how to solve the problem create these problems. A good example is the issue of expansion shocks, which can be seen by taking Sod’s shock tube and introducing a velocity to the initial condition. This puts a sonic point (where the characteristic speed goes to zero) in the rarefaction. We know how to remove this problem by adding an “entropy” fix to the Riemann solver defining a class of methods that work. The test simply unveils whether the problem infests a code that may have ignored this issue. This detection is a very good side-effect of a well-designed test problem.

Another great example is the carbuncle instability where mesh aligned shock wave exhibit and symmetry breaking bounded instability. This problem was seen first in blunt body simulation of re-entry vehicles, but inhabits frightfully many simulations in a host of applications. The issue still remains inadequately solved although some remedies exist, none is fully satisfactory. The progress made to date has largely arisen through its more clear identification and the production of simplified test problems that exhibit its fundamental behavior. In my own experience if a code doesn’t explicitly stabilize the carbuncle instabilities, the problem will be present and manifest itself. These manifestations will often be subtle and difficult to detect often masquerading as valid physical effects. A good test problem will expose the difficulty and force the code to be robust to it.

One of the best carbuncle exposing problems simply propagates a strong shock wave in one dimension, hardly a challenge today. The wrinkle in the problem is to make the problem two or three dimensional even though the extra dimensions should be ignorable. It introduces a small perturbation to the problem and tests whether the shock wave induces an unphysical growth in the resulting solution. Codes that exhibit the carbuncle instability allow the perturbations to grow and ultimately corrupt the solution. The problem is simple and elegant, but brutally effective for the purpose it was designed. It was inspired by the path to successful analysis of the core issues leading to the carbuncle instability.

The key idea to the modeling and simulation enterprise is identifying problems that expose weaknesses in current methods and codes. Once these weaknesses are addressed they provide a codec of wisdom about problems that have solved, and whether such wisdom was accounted for in a new method or code. New problems working at the boundaries of our knowledge are needed to push the community and spur progress. Meaningful progress can be measured through the conversion of such challenging problems from those that break methods and codes, to reasonable solution by methods and codes, and finally to accurate solution. When a problem has moved from a threat to success, it is time to create a new harder problem to continue progress.

Ultimately the brutal problems are an admission of where the method or code is vulnerable. This reflects on the personal vulnerability of those who professionally associated themselves with the code. This makes testing the code rigorously and brutally impossibly hard especially in today’s “no failure allowed” accountability culture. Its much easier to simply stop where everything appears to work just fine. Brutal problems spur growth, but also challenge our belief of mastery and success. It takes strong people to continually confront the boundaries of their knowledge and capability push it back, and confront it anew over and over.

At a deeply personal level testing codes becomes an exercise in leaving one’s comfort zone. The comfort zone is where you know how to solve problems, and you feel like you have mastery of things. Breaking your code, fixing it and breaking it again is a process of stepping out of the comfort zone as a principle in energizing progress. In my experience we have a culture that increasingly cannot deal with failure successfully. We must always succeed and get punished mercilessly for failure. Risk must be identified and avoided at all costs. The comfort zone is success, and for codes this looks like successful operation, and bona fide healthy convergence all of which is provided by easy problems. Brutal problems expose not just code weaknesses, but personal weakness and intellectual failings or gaps. Rather than chase personal excellence we are driven to choose comfortable acquiescence to the status quo. Rather than be vulnerable and admit our limitations, we choose comfort and false confidence.

Vulnerability is the birthplace of love, belonging, joy, courage, empathy, and creativity. It is the source of hope, empathy, accountability, and authenticity. If we want greater clarity in our purpose or deeper and more meaningful spiritual lives, vulnerability is the path.

― Brené Brown

Sod, Gary A. “A survey of several finite difference methods for systems of nonlinear hyperbolic conservation laws.” Journal of computational physics 27, no. 1 (1978): 1-31.

Pember, R. B., and R. W. Anderson. A Comparison of Staggered-Mesh Lagrange Plus Remap and Cell-Centered Direct Eulerian Godunov Schemes for Rulerian Shock Hydrodynamics. No. UCRL-JC-139820. Lawrence Livermore National Lab., CA (US), 2000.

Gottlieb, J. J., and C. P. T. Groth. “Assessment of Riemann solvers for unsteady one-dimensional inviscid flows of perfect gases.” Journal of Computational Physics 78, no. 2 (1988): 437-458.

Munz, C‐D. “A tracking method for gas flow into vacuum based on the vacuum Riemann problem.” Mathematical methods in the applied sciences 17, no. 8 (1994): 597-612.

Quirk, James J. “A contribution to the great Riemann solver debate.” In Upwind and High-Resolution Schemes, pp. 550-569. Springer Berlin Heidelberg, 1997.

 

Simply, in a word, NO, I’m not productive.

Most of us spend too much time on what is urgent and not enough time on what is important.

― Stephen R. Covey

A big part of productivity is doing something worthwhile and meaningful. It means attacking something important and creating innovative solutions. I do a lot of things every day, but very little of it is either worthwhile or meaningful. At the same time I’m doing exactly what I am supposed to be doing! This means that my employer (or masters) are asking me to spend all of my valuable time doing meaningless, time wasting things as part of my conditions of employment. This includes trips to stupid, meaningless meetings with little or no content of value, compliance training, project planning, project reports, e-mails, jumping through hoops to get a technical paper, and a smorgasbord of other paperwork. Much of this is hoisted upon us by our governing agency, coupled with rampant institutional over-compliance, or managerially driven ass covering. All of this equals no time or focus on anything that actually matters squeezing out all the potential for innovation. Many of the direct actions result in creating an environment where risk and failure are not tolerated thus killing innovation before it can attempt to appear.

Worse yet, the environment designed to provide “accountability” is destroying the very conditions innovative research depends upon. Thus we are completely accountable for producing nothing of value.

Every single time I do what I supposed to do at work my productivity is reduced. The only thing not required of me at work is actual productivity. All my training, compliance, and other work activities are focused on things that produce nothing of value. At some level we fail to respect our employees and end up wasting our lives by having us invest time in activities devoid of content and value. Basically the entire apparatus of my work is focused on forcing me to do things that produce nothing worthwhile other than providing a wage to support my family. Real productivity and innovation is all on me and increasingly a pro bono activity. The fact that actual productivity isn’t a concern for my employer is really fucked up. The bottom line is that we aren’t funded to do anything valuable, and the expectations on me are all bullshit and no substance. Its been getting steadily worse with each passing year too. When my employer talks about efficiency, it is all about saving money, not producing anything for the money we spend. Instead of focusing on producing more or better with the funding and unleashing the creative energy of people, we focus on penny pinching and making the workplace more unpleasant and genuinely terrible. None of the changes make for a better, more engaging workplace and simply continually reduce the empowerment of employees.

One of the big things to get to is what is productive in the first place?

There is nothing quite so useless, as doing with great efficiency, something that should not be done at all.

― Peter F. Drucker

Productivity is creating ideas and things whether it is science or art. Done properly science is art. I need to be unleashed to provide value for my time. Creativity requires focus and inspiration making the best of opportunities provided by low hanging fruit. Science can be inspired by good mission focus producing clear and well-defined problems to solve. None of these wonderful things is the focus of efficiency or productivity initiatives today. Every single thing my employer does put a leash on me, and undermines productivity at every turn. This leash is put into a seemingly positive form of accountability, but never asks or even allows me to be productive in the slightest.

Poorly designed and motivated projects are not productive. Putting research projects into a project management straightjacket makes everything worse. We make everything myopic and narrow in focus. This kills one of the biggest sources of innovation. Most breakthroughs aren’t totally original, but rather the adaptation of a mature idea from one field into another. It is almost never a completely original thing. Our focused and myopic management destroys the possibility of these innovations. Increasingly our projects and proposals are all written to illicit funding, not produce the best results. We produce a system that focuses on doing things that are low risk and nearly guaranteed payoff, which results in terrible outcomes where progress is incremental at best. The result is a system where I am almost definitively not productive if I do exactly what I’m supposed to do. The entire apparatus of accountability is absurd and an insult to productive work. It sounds good, but its completely destructive, and we keep adding more and more of it.

Why am I wasting my time, I could produce so much with a few hours of actual work. I read article after article that says I should be able to produce incredible results working only four hours a day. The truth is that we are creating systems at work that keep us from doing anything productive at all. The truth is that I have to go to incredible lengths to get anything close to four hours of actual scientific focus time. We are destroying the ability for us to work effectively all in the name of accountability. We destroy work in the process of assuring that work is getting done. Its ironic, its tragic, and its totally unnecessary.

If you want something new, you have to stop doing something old

― Peter F. Drucker

The key is how do we get the point of not wasting my time with this shit? Accountability sounds good, but underneath its execution is a deep lack of trust. The key to allowing me to be productive is to trust me. We need to realize that our systems at work are structured to deal with a lack of trust. Implicit in all the systems is a feeling that people need to be constantly being checked up on. If people aren’t constantly being checked up on they are fucking off. The result is an almost complete lack of empowerment, and a labyrinth of micromanagement. To be productive we need to be trusted, and we need to be empowered. We need to be chasing big important goals that we are committed to achieving. Once we accept the goals, we need to be unleashed to accomplish them. In the process we need to solve all sorts of problems, and in the process we can provide innovative solutions that enrich the knowledge of humanity and enrich society at large. This is a tried and true formula for progress that we have lost faith in, and with this lack of faith we have lost trust in our fellow citizens.

The whole system needs to be oriented toward the positive and away from the underlying premise that people cannot be trusted. This goes hand in hand with the cult of the manager today. If one looks at the current organizational philosophy, the manager is king and apex of importance. Work is to be managed and controlled. The workers are just cogs in the machine, interchangeable and utterly replicable. To be productive, the work itself needs to be celebrated and enabled. The people doing this work need to be the focus of the organization and getting wonderful work done enabled by its actions. The organization needs to enable and support productive work, and create an environment that fosters the best in people. Today’s organizations are centered on expecting and controlling the worst in people with the assumption that they can’t be trusted. If people are treated like they can’t be trusted, you can’t expect them to be productive. To be better and productive, we need to start with a different premise. To be productive we need to center and focus our work on the producers, not the managers. We need to trust and put faith in each other to solve problems, innovate and create a better future.

To be happy we need something to solve. Happiness is therefore a form of action;

― Mark Manson