Question, Analyze, Understand and Create,… Repeat

28 Friday Jul 2017

We don’t receive wisdom we must discover it for ourselves.

― Marcel Proust

Work is best when you start with a good question, analyze and learn until you discover and understand an answer to the question (questions often have many answers). Then you use this understanding to create something wonderful so that you can find a new and better question to answer. This virtuous cycle leads to be best work and provides the foundation for excellence. It is precisely the recipe for the best work experiences I’ve had, built my expertise and definitely how I’d prefer to keep doing work.

I’m on vacation this week (San Francisco is an amazing city!) and it is the perfect opportunity to think deeply about life and work. Work is an extremely important part of life, and I’ve concluded that some key things determine whether or not it is really good. The same things determine your ability to achieve excellence. What I’ve observed is a process that takes place leading up to my happiness and satisfaction. More importantly, it leads to great work, productivity and excellence. The elements of this successful recipe are founded on attacking a question that needs to be answered. This question can either come from something larger than myself, or simple innate personal curiosity. At the end of the process the question has been refined and answered yielding new understanding, knowledge, learning and tools to create something better. For me, the act of creation is the ultimate in job satisfaction for me. This is a virtuous cycle that leads to deep knowledge and the ability to recycle this process with an even better question using what has been learned and created.

Our real discoveries come from chaos, from going to the place that looks wrong and stupid and foolish.

― Chuck Palahniuk

The largest portion and most important part of this process is the analysis that allows us to answer the question. Often the question needs to be broken down into a series of simpler questions some of which are amenable to easier solution. This process is hierarchical and cyclical. Sometimes the process forces us to step back and requires us to ask an even better or more proper question. In sense this is the process working in full with the better and more proper question being an act of creation and understanding. The analysis requires deep work and often study, research and educating oneself. A new question will force one to take the knowledge one has and combine it with new techniques producing enhanced capabilities. This process is on the job education, and fuels personal growth and personal growth fuels excellence. When you are answering a completely new question, you are doing research and helping to push the frontiers of science forward. When you are answering an old question, you are learning and you might answer the question in a new way yielding new understanding. At worst, you are growing as a person and professional.

This is an utterly noble endeavor and embodies the best of mankind. At times you are simply pushing your self forward into areas others know very well already, but to you it is fresh and new. This is OK and even essential to get to the place where your work is unique. An under appreciated aspect of this sort of learning is the path you take is the potential to learn things in new ways. Your path is likely to be different than anyone else’s and grafts your own experience and understanding on to the topic anew. This is immensely valuable and can unveil new paths and depth to existing knowledge. Today this sort of thing is wholly unsupported and under appreciated. We need to make a new commitment to use this path to excellence.

The real voyage of discovery consists not in seeking new landscapes, but in having new eyes.

― Marcel Proust

Sometimes the question being answered has been well studied and one is simply discovering knowledge others have already mastered. This is important growth for a professional getting to the point where the frontier of knowledge exists. This is a necessary element in getting to research, which doesn’t happen automatically. One needs to climb up the mountain of human knowledge before getting to the apex. This is the process of education as a professional and an immensely exciting calling. The mastery of a topic requires many essential elements be mastered drawing together knowledge from diverse forces. Often the best research draws together rather pedestrian bits of knowledge from diverse fields in novel manners heretofore unseen before. When we don’t support this sort of endeavor, we smother important avenues of discovery and deny our society of the most important discoveries. Charting new paths to knowledge is either a wondrous personal journey and/or an alternative way to understand.

Discovery consists of looking at the same thing as everyone else and thinking something different.

― Albert Szent-Györgyi

Ultimately the elements are drawn together and allow the question to be answered productively. This often produces a new kernel of understanding. This knowledge can often be harnessed to produce the wherewithal for something new. The understanding will allow a new and unique act of creation. Sometimes you are creating something that others already know about, but for you it is new. That is enough for excellence; it is the engine of personal excellence. If you complete this cycle often enough eventually the creation will be genuinely original and new. The deep and powerful educational elements of this process leads to outstanding professionals well before one gets to genuinely new and unique research. It is essential to realize that very few creations are completely original with most discoveries being the combination of elements that are well known in other applications. In many cases the analysis and study of the answer to the original question itself creates something new and wonderful of many forms.

What is wanted is not the will to believe, but the will to find out, which is the exact opposite.

― Bertrand Russell

Once this creation is available, new questions can be posed and solved. These creations allow new questions to be asked answered. This is the way of progress where technology and knowledge builds the bridge something better. If we support excellence and a process like this, we will progress. Without support for this process, we simply stagnate and whither away. The choice is simple either embrace excellence by loosening control, or chain people to mediocrity.

Science is the process that takes us from confusion to understanding…

― Brian Greene

The Foundations of Verification: Solution Verification

21 Friday Jul 2017

Posted by Bill Rider in Uncategorized

≈ 1 Comment

A very great deal more truth can become known than can be proven.

― Richard Feynman

Solution verification involves examining error and results without the knowledge the imgres exact solution. This makes it a more difficult task than code verification where an exact solution is known removing a major uncertainty. A secondary issue associated with not knowing the exact solution is the implications on the nature of the solution itself. With an exact solution, a mathematical structure exists allowing the solution to be achievable analytically. Furthermore, exact solutions are limited to relatively simple models that often cannot model reality. Thus, the modeling approach to which solution verification is applied is necessarily more complex. All of these factors are confounding and produce a more perilous environment to conduct verification. The key product of solution verification is an estimate of numerical error and the secondary product is the rate of convergence. Both of these quantities are important to consider in the analysis.

The way to cope with this generally more hostile analysis environment involves improved analysis methods. One of the key elements in the analysis is contending with the lack of certainty about the solution, its nature and character mathematically. For this reason the knowledge and guarantees about the results is missing. For instance we don’t know what order of convergence to reasonably expect from the analysis and cannot use this to screen our results. Generally speaking if the verification result shows convergence at the theoretical rate for the method we can be sure we are solving a relatively simple “easy” problem. Usually the applied problems that modeling & simulation are attacking are mathematically difficult. Philosophically, the whole reason for modeling & simulation is solving problems that are beyond our analytical grasp. In a deep sense the complex and difficult character to problems is unavoidable for the practical a use of modeling with computers. When we’ve successfully attacked the problem of verification for a problem without an exact solution, the same analysis methodology can improve our code verification practice. chart-with-huge-error-bars

It is important to understand solution verification within the broader context of computational modeling. Solution verification contributes to the overall enterprise of analysis uncertainty quantification. The most classical investigation will involve comparing the modeled results with observations in the real World (ideally an experiment). There are many elements to the uncertainty in this case including the model parameters, the constitutive properties, the experimental measurements and the numerical solution. Solution verification is the process for examining and estimating the numerical error and specifying its uncertainty. Sometimes this is applied in the use of computational modeling for purposes of decision-making or scenario testing where no real World data exists. In this case the numerical error is an important element in the overall lack of certainty about the results. If the numerical error is well behaved it will be a bias from the exact continuum solution to the model. This bias is important to understand in how it might skew the results and any advise.

There are two ways to do great mathematics. The first is to be smarter than everybody else. The second way is to be stupider than everybody else — but persistent.

― Raoul Bott

When one lays out the mathematical framework for solution verification, the immediate impression is the added difficulty compared to code verification is the lack of direct knowledge of the precise solution. The full solution to the problem is inferred from the inaccurate numerical solutions. The equation to solve is the following $S_0 = S_k + C h_k^a$ where the new unknown is the obstensible estimate of the exact solution $S_0$ that is the solution where $h=0$ . The solutions used to determine this estimate are $S_k$ the solutions found with $h_k$ . We notice that we have images three unknowns, $S_0, C, a$ meaning the well-determined solution requires three pieces of determined data, $S_k$ . As we will discuss this problem can be solved in a variety of ways including under-, fully and over-determined forms.

One of the key issues to recognize with solving this problem is an aspect of complexity because of the general nonlinearity of the determination of the model. The solution to this coupled system of nonlinear equations is generally subtle, and necessarily solved numerically. As such, the solution can have its own errors requiring some care and verification. The system of equations admits a simple analytical solution in special cases where the discrete solutions use a sequence of meshes where $r = h_k/h_{k-1}$ is constant. In this case we can write the solution in closed form $\log (E_{1,2}/E_{2,3}) / \log (r)$ , where $E_{k,k-1} = S_k - S_{k-1}$ . More generally we need to attack this with a coupled nonlinear solve. If we deal with an over-determined version of the problem we will use a nonlinear least squares solver (or this is the knee-jerk response). As we discuss next, thinking about this decision opens the door to some more interesting and robust choices.

The general over-determined version of the solution verification equation (i.e., more than three grids) would be amenable to solution via nonlinear least squares method. This is not the only choice, and consideration of this opens the door to other choices. The solution to the over-determined problem is not unique, and the solution has the imprint of the method of solution. As such the choice of least squares implies a number of explicit assumptions that the typical practitioner doesn’t even know they are making. For example, one may choose to solve the over-determined problem in a different norm than the two norm (i.e., least squares). One may choose to solve a constrained problem instead of an unconstrained problem. In addition, one could consider solving an under-determined problem adding either constraints or regularizing the solution. A classical example of regularization is the Tikhonov method where a penalty is added to make the problem well determined. A popular recent approach focuses on a similar regularization, but in the one norm (compressed sensing, LASSO, …).

mediocritydemotivator There are several practical issues related to this whole thread of discussion. One often encountered and extremely problematic issue is insanely high convergence rates. After one has been doing verification or seeing others do verification for a while, the analysis will sometimes provide an extremely high convergence rate. For example a second order method used to solve a problem will produce a sequence that produces a seeming 15^th order solution (this example is given later). This is a ridiculous and results in woeful estimates of numerical error. A result like this usually indicates a solution on a tremendously unresolved mesh, and a generally unreliable simulation. This is one of those things that analysts should be mindful of. Constrained solution of the nonlinear equations can mitigate this possibility and exclude it a priori. This general approach including the solution with other norms, constraints and other aspects is explored in the paper on Robust Verification. The key concept is the solution to the error estimation problem is not unique and highly dependent upon assumptions. Different assumptions lead to different results to the problem and can be harnessed to make the analysis more robust and impervious to issues that might derail it.

The techniques discussed in that paper were originally devised to deal with the all too often case where only one or two different grids are used and the error estimation problem is under-determined. The approach taken to solve this problem involves adding constraints to the solution based on expert knowledge and judgment. The overall approach was then approached when it was realized that the under- fully- and over-determined cases should all be treated consistently. The verification problem is solved repeatedly using different assumptions resulting in a natural variation in the results providing uncertainty in the error estimation and the rate of convergence. If the data is self consistent with a well-defined solution the uncertainty in the error will itself be small and the convergence rate will also be certain. Conversely if the data is conflicting or opposes expert expectations, the uncertainty will be large. This entire methodology produces a more robust numerical uncertainty that adapts to the data, and avoids using fixed size safety factors. It turns out that this expert judgment is usually called into action with verification, but in an ad hoc manner and only when the issues are serious. The robust verification adds the expert judgment from the outset so that more subtle issues are subject to the same treatment.

Instead of solving the verification equation once using a nonlinear least squares approach, robust verification solves the problem in a multitude of ways. This involves solving the verification problem using other error norms in a constrained minimization framework. The data is also used over. One standard assumption is that the solutions on the finer grids (smaller $h$ ) are closer to the exact solution, and this data is more prominent in the solution. The end result of the analysis is a multitude of estimates of the numerical error and convergence. These results are then subjected to robust statistical examination using median statistics. We report the median of the estimates as the error and convergence rate. The median deviation is used to place and uncertainty on this estimate. One of the key benefits of this estimation is its lack of susceptibility to corruption by outliers in the analysis. Outliers are further suppressed in the analysis by the use of expert judgment as constraints. For example, the absurdly large convergence rates are removed by the constraints if the rate of convergence is constrained to be below a given value.

forwardEuler Before moving to examples of solution verification we will show how robust verification can be used for code verification work. Since the error is known, the only uncertainty in the analysis is the rate of convergence. As we can immediately notice that this technique will get rid of a crucial ambiguity in the analysis. In standard code verification analysis, the rate of convergence is never the exact formal order, and expert judgment is used to determine if the results is close enough. With robust verification, the convergence rate has an uncertainty and the question of whether the exact value is included in the uncertainty band can be asked. Before showing the results for this application of robust verification, we need to note that the exact rate of verification is only the asymptotic rate in the limit of $h = 0$ . For a finite step size the rate of convergence should deviate from this value and for simple cases the value can be derived using a modified version of classical numerical analysis.

Our first example of solution verification will repeat our examination of simple ODE integrators, but disregard our knowledge of the exact solution. It is a useful example because we can examine the efficacy of solution verification with a precise knowledge of the true errors. We can use the data from our code verification study to good effect here. Here is the raw data used for the forward Euler study.

h	Solution, t=1	Error, t=1
0.20	0.3277	0.0402
0.10	0.3487	0.0192
0.05	0.3585	0.0094
0.02	0.3642	0.0037
0.01	0.3660	0.0018
estimate	0.3678±0.0002

For the code verification part of the example, the estimated truncation error is $E=0.2030 h^{1.0245\pm0.0124}$ . The error bars do not take us to the theoretical convergence rate of one. The data is consistent with the rate being above one (and this is analytically expected). Using this same data for solution verification yields the following model, $S(h) = 0.3678 \pm 0.0002 - 0.2080 h^{1.0386 \pm 0.0207}$ . Close examination shows that this solution is quite close to the exact solution 0.0001 and within the error bars. If we use the standard techniques of simply least square fitting the data we get the following model, $S(h) = 0.3677 - 0.2239 h^{1.0717}$ . The error estimate here is 0.0017, which ends up being rather over generous when the standard safety factor of 1.25 is applied. Using the robust verification technique we get a better estimate of the exact solution, the actual convergence rate and a tighter error bound.

Supposing is good, but finding out is better.

― Mark Twain

It is also useful to look at a pathological case where the rate of convergence is absurd and standard analysis would be prone to missing it. The case we have at our fingertips involved very coarse grid solutions to large eddy simulation in a complex geometry relevant to heat transfer and fluid flow in nuclear reactors. Early calculations were used to estimate the mesh required for well-resolved calculations. As we found out, this is a perilous enterprise. A couple codes (one production and one research) we enlisted in thi rodbundle s study using some initial grids that were known to be inadequate. One of the codes was relatively well trusted for this class of applications and produced three solutions that for all appearances appeared reasonable. One of the key parameters is the pressure drop through the test section. Using grids 664K, 1224K and 1934K elements we got pressure drops of 31.8 kPa, 24.6 kPa and 24.4 kPa respectively. Using a standard curve fitting for the effective mesh resolution gave an estimate of 24.3 kPa±0.0080 kPa for the resolved pressure drop and a convergence rate of 15.84. This is an absurd result and needs to simply be rejected immediately. Using the robust verification methodology on the same data set, gives a pressure drop of 16.1 kPa±13.5 kPa with a convergence rate of 1.23, which is reasonable. Subsequent calculations on refined grids produced results that were remarkably close to this estimate confirming the power of the technique even when given data that was substantially corrupted.

drekar Our final example is a simple case of validation using the classical phenomena of vortex shedding over a cylinder at a relatively small Reynolds number. This is part of a reasonable effort to validate a research code before using in on more serious problems. The key experimental value to examine is the Stouhal number defined, $St = f \ell/U$ the shedding frequency normalized by the size of cylinder and the velocity, which has the value experimentally of $0.164\pm 0.005$ for a flow of Reynolds number 100 (the Reynolds number is the non-dimensional ratio of inertial to viscous force in a flow).

∆t	RMS h	St
0.002	0.054111988	0.110474853
0.002	0.023801688	0.152492294
0.002	0.010786082	0.164777976
0.002	0.005264375	0.165127187

When we apply the robust verification methodology to this data we find that the code produces a Strouhal number that is slightly larger than the experimental value $St(h) = 0.1657\pm 0.0013 + C h^{1.8486\pm 0.1476}$ . Including error bars recovers the experimental value. This can be regarded as a modest success for the code’s ability to be considered for more complex flows.

The foundation of data gathering is built on asking questions. Never limit the number of hows, whats, wheres, whens, whys and whos, as you are conducting an investigation. A good researcher knows that there will always be more questions than answers.

― Karl Pippart III

Rider, William, Walt Witkowski, James R. Kamm, and Tim Wildey. “Robust verification analysis.” Journal of Computational Physics 307 (2016): 146-163.

The Foundations of Verification: Code Verification

14 Friday Jul 2017

Posted by Bill Rider in Uncategorized

≈ Leave a comment

A very great deal more truth can become known than can be proven.

― Richard Feynman

In modeling and simulation verification is a set of activities broadly supporting the quality. Verification consists of two modes of practice: code verification where the mathematical correctness of the computer code is assessed, or solution (calculation) verification where the numerical error (uncertainty) is estimated. Both activities are closely linked to each other and they are utterly complementary in nature. To a large extent the methodology used for both types of verification are similar, but the differences between the two are important to maintain.

Modeling and simulation is an activity where continuous mathematics is converted to discrete computable quantities. This process involves approximation of the continuous mathematics and in almost every non-pathological circumstance is inexact. The core of modeling and simulation is the solution of (partial) differential equations using approximation methods. Code verification is a means of assuring that the approximations used to make the discrete solution of differential equations tractable on a computer are correct. A key aspect of code verification is determining that the discrete approximation of the differential equation is consistent with the continuous version of the differential equation.

Consistency demands that the order of approximation of the differential equation be at least one. In other words the discrete equations produce solutions that are the original continuous equations plus terms that are proportional to the size of the discretization. This character may be examined by solving problems with an exact analytical solution (or a problem with very well controlled and characterized errors) using several discretization sizes allowing the computation of errors, and determining the order of approximation. The combination of consistency and stability of the approximation means the approximation converges to the correct solution of the continuous differential equation.

We will examine both the nature of different types of problems to determine code verification and the methods of determining the order of approximation. One of the key aspects of code verification is the congruence of the theoretical order of accuracy for a method, and the observed order of accuracy. It is important to note that the theoretical order of convergence also depends upon the problem being solved. The problem must possess enough regularity to support the convergence rate expected. At this point it is important to point out that code verification produces both an order of approximation and an observed error in solution. Both of these quantities are important. For code verification, the order of approximation is the primary quantity of interest. It depends on both the nature of the approximation method and the problem being solved. If the problem being solved is insufficiently regular and smooth, the order of accuracy will not match the theoretical expectations of the method.

The second form of verification is solution verification. This is quite similar to code verification, but its aim is the estimation of approximation errors in a calculation. When one runs a problem without an analytical solution, the estimation of errors is more intricate. One looks at a series of solutions and compute the solution that is indicated by the sequence. Essentially the question of what solution is the approximation appearing to converge toward is being asked. If the sequence of solutions converges, the error in the solution can be inferred. As with code verification the order of convergence and the error is a product of the analysis. Conversely to the code verification, the error estimate is the primary quantity of interest, and the order of convergence is secondary.

The approach, procedure and methodology for both forms of verification are utterly complementary. Much of the mathematics and flow of work are shared in all verification, but details, pitfalls and key tips differ. In this post the broader themes of commonality are examined along with distinctions and a general rubric for each type of verification is discussed.

Code verification

Science replaces private prejudice with public, verifiable evidence.

― Richard Dawkins

When one conducts a code verification study there is a basic flow of activities and practices to conduct. One looks at a code to target and a problem to solve. Several key bits of information should be immediately being focused upon before the problem is solved. What is the order of accuracy for the method in the code being examined, and what is the order of accuracy that the problem being solved can expose? In addition the nature of the analytical solution to the problem should be carefully considered. For example what is the nature of the solution? Closed form? Series expansion? Numerical evaluation? Some of these forms of analytical solution have errors that must be controlled and assessed before the code’s method may be assessed. By the same token are there auxiliary aspects of the code’s solution that might pollute results? Solution of linear systems of equations? Stability issues? Computer roundoff or parallel computing issues? In each case these details could pollute results if not carefully excluded from consideration.

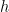Next one needs to produce a solution on a sequence of meshes. For simple verification using a single discretization parameter only two discretizations are needed for verification (two equations to solve for two unknowns). For code verification the model for error is simple, generally a power law, $E = A h^a$ where the error is proportional to the discretization parameter $h$ to the power (order) $a$ . There is also a constant of proportionality. The order, $a$ is the target of the study and one looks at its congruence with the expected theoretical order for the method on the problem being solved. It is almost always advisable to use more than the minimum number of meshes to assure that one simply isn’t examining anamolous behavior from the code.

One of the problems with code verification is the rarity of the observed order of convergence to exactly match the expected order of convergence. The question of how close is close enough haunts investigations. Invariably the observed order will deviate from the expected order by some amount. The question for the practitioner is how close is acceptable? Generally this question is given little attention. There are more advanced verification techniques that can put this issue to rest by producing uncertainties on the observed order, but the standard techniques simply produce a single result. Usually this results in rules of thumb that apply in broad brushes, but undermine the credibility of the whole enterprise. Often the criterion is that the observed order should be within a tenth of the theoretically expected result.

Another key caveat comes up when the problem is discontinuous. In this case the observed order is either set to one for nonlinear solutions, or weakly tied to the theoretical order of convergence. For the wave equation this result was studied by Banks, Aslam and Rider and admits an analytical and firmly determined result. In both cases the issue of inexact congruence with the expected rate of convergence remains. In addition for problems involving systems of equations will have multiple features each having a separate order of convergence, and the rates will combine within a solution. Ultimately in an asymptotic sense the lowest order of convergence will dominate as 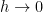$h \rightarrow 0$ . This is quite difficult to achieve practically.

The last major issue that comes up in code verification (and solution verification too) is the nature of the discrete mesh and its connection to the asymptotic range of convergence. All of the theoretical results apply when the discretization parameter is small in a broad mathematical sense. This is quite problem specific and generally ill defined. Examining the congruence of the numerical derivatives of the analytical solution with the analytical derivatives can generally assess this. When these quantities are in close agreement, the solution can be considered to be asymptotic. Again these definitions are loose and generally applied with a large degree of professional or expert judgment.

It is useful to examine these issues through a concrete problem in code verification. The example I’ll use is a simple ordinary differential equation integrator for a linear equation $u_t = - u$ coded up in Mathematica. We could solve this problem in a spreadsheet (like MS Excel), python, or a standard programming language. The example will look at two first order methods, forwards $u^{n+1} + h u^n$ $=u^{n}$ and backwards $u^{n+1} + h u^{n+1} = u^n$ Euler methods. Both of these methods produce leading first order errors in an asymptotic sense, $E = C h + O(h^2)$ . 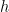If $h$ is large enough, the high order terms will pollute the error and produce deviations from the pure first-order error. Let’s look at this example and the concrete analysis from verification. This will be instructive in getting to similar problems encountered in general code verification.

Here is the code

ForwardEuler[h_, T_, a_] :=

(

uo = 1;

t = 0.0;

While[t < T,

(* integration *)

t = t + h;

un = uo + a h uo;

Print[“t= “, t, ” u(t) = “, un, ” err = “, Abs[un – Exp[a t]]];

uo = un

];

)

BackwardEuler[h_, T_, a_] :=

(

uo = 1;

t = 0.0;

While[t < T,

(* integration *)

t = t + h;

un = uo/(1 + a h);

Print[“t= “, t, ” u(t) = “, un, ” err = “, Abs[un – Exp[a t]]];

uo = un

];

)

Let’s look at the forward Euler integrator for several different choices of 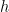$h$ , different end times for the solution and number of discrete solutions using the method. We will do the same thing for the backwards Euler method, which is different because it is unconditionally stable with respect to step size. For this simple ODE, the method is stable to a stepsize of $h=2$ and we can solve the problem to two stopping times of $T=1.0$ , $T=10.0$ and $T=100.0$ . The analytical solution is always, $u(T) = \exp^{-T}$ . We can solve this problem using a set of step sizes, $h=1.0, h=0.5, h=0.25, h=0.125$ .

I can give results for various pairs of step sizes with both integrators, and see some common pathologies that we must deal with. Even solving such a simple problem, with simple methods can prove difficult and prone to heavy interpretation (arguably the simplest problem with the simplest methods). Much different results are achieved when the problem is run until different stopping times. We see the impactof accumulated error (since I’m using Mathematica so aspects of round-off error are pushed aside). In these cases round-off error would be another complication. Furthermore the backward Euler method for multiple equations would involve a linear (or nonlinear) solution that itself has an error tolerance that may significantly impact verification results. We see good results for $T=1.0$ and a systematic deviation for longer ending times. To get acceptable verification results would require much smaller step sizes (for longer calculations!). This shows how easy it is to scratch the surface of really complex behavior in verification that might mask correctly implemented methods. What isn’t so well appreciated is that this behavior is expected and amenable to analysis through standard methods extended to look for it.

h	FE T=1	FE T=10	FE T=100	BE T=1	BE T=10	BE T=100
1	1.64	0.03	~0	0.79	1.87	16.99
0.5	1.20	0.33	4e-07	0.88	1.54	11.78
0.25	1.08	0.65	0.002	0.93	1.30	7.17
0.125	1.04	0.83	0.05	0.96	1.16	4.07
0.0625	1.02	0.92	0.27	0.98	1.08	2.40
0.03125	1.01	0.96	0.55	0.99	1.04	1.63

Computed order of convergence for forward Euler (FE) and backward Euler (BE) methods for various stopping times and step sizes.

Types of Code Verification Problems and Associated Data

Don’t give people what they want, give them what they need.

― Joss Whedon

The problem types are categorized by the difficulty of providing a solution coupled withthe quality of the solution that can be obtained. These two concepts go hand-in-hand. As simple closed form solution is easy to obtain and evaluation. Conversely, a numerical solution of partial differential equations is difficult and carries a number of serious issues regarding its quality and trustworthiness. These issues are addressed by an increased level of scrutiny on evidence provided by associated data. Each of benchmark is not necessarily analytical in nature, and the solutions are each constructed in different means with different expected levels of quality and accompanying data. This necessitates the differences in level of required documentation and accompanying supporting material to assure the user of its quality.

Next, we provide a list of types of benchmarks along with an archetypical example of each. This is intended to be instructive to the experienced reader, who may recognize the example. The list is roughly ordered in increasing level of difficulty and need for greater supporting material.

Closed form analytical solution (usually algebraic in nature). Example: Incompressible, unsteady, 2-D, laminar flow over an oscillating plate (Stokes oscillating plate) given in Panton, R. L. (1984). Incompressible Flow, New York, John Wiley, pp. 266-272.
Analytical solution with significantly complex numerical evaluation
- Series solution. Example: Numerous classical problems, in H. Lamb’s book, “Hydrodynamics,” Dover, 1932. Classical separation of variables solution to heat conduction. Example: Incompressible, unsteady, axisymmetric 2-D, laminar flow in a circular tube impulsively started (Szymanski flow), given in White, F. M. (1991). Viscous Fluid Flow, New York, McGraw Hill, pp. 133-134.
- Nonlinear algebraic solution. Example: The Riemann shock tube problem, J. Gottleib, C. Groth, “Assessment of Riemann solvers for unsteady one-dimensional inviscid flows of perfect gases,” Journal of Computational Physics, 78(2), pp. 437-458, 1988.
- A similarity solution requiring a numerical solution of nonlinear ordinary differential equations.
- Manufactured Solution. Example: Incompressible, steady, 2-D, turbulent, wall-bounded flow with two turbulence models (makes no difference to me), given in Eça, L., M. Hoekstra, A. Hay and D. Pelletier (2007). “On the construction of manufactured solutions for one and two-equation eddy-viscosity models.” International Journal for Numerical Methods in Fluids. 54(2), 119-154.
Highly accurate numerical solution (not analytical). Example: Incompressible, steady, 2-D, laminar stagnation flow on a flat plate (Hiemenz flow), given in White, F. M. (1991). Viscous Fluid Flow, New York, McGraw Hill. pp. 152-157.
Numerical benchmark with an accurate numerical solution. Example: Incompressible, steady, 2-D, laminar flow in a driven cavity (with the singularities removed), given in Prabhakar, V. and J. N. Reddy (2006). “Spectral/hp Penalty Least-Squares Finite Element Formulation for the Steady Incompressible Navier-Stokes Equations.” Journal of Computational Physics. 215(1), 274-297.
Code-to-code comparison data. Example: Incompressible, steady, 2-D, laminar flow over a back-step, given in Gartling, D. K. (1990). “A Test Problem for Outflow Boundary Conditions-Flow Over a Backward-Facing Step.” International Journal for Numerical Methods in Fluids. 11, 953-967.

Below is a list of the different types of data associated with verification problems defined above. Depending on the nature of the test problem only a subset of these data are necessary. This will be provided below the list of data types. As noted above, benchmarks with well-defined closed form analytical solutions require relatively less data than a benchmark associated with the approximate numerical solution of PDEs.

Detailed technical description of the problem (report or paper)
Analysis of the mathematics of the problem (report or paper)
Computer analysis of solution (input file)
Computer solution of the mathematical solution
Computer implementation of the numerical solution
Error analysis of the “exact” numerical solution
Derivation of the source term and software implementation or input
Computer implementation of the source term (manufactured solution)
Grids for numerical solution
Convergence and error estimation of approximate numerical solution
Uncertainty and sensitivity study of numerical solution
Description and analysis of computational methods
Numerical analysis theory associated with convergence
Code description/manuals
Input files for problems and auxiliary software
Patch test description, Derivation, input and analysis
Unusual boundary conditions (inflow, piston, etc.…)
Physics restrictions (boundary layer theory, inviscid,)
Software quality documents
Scripts and auxiliary software for verification
Source code
Metric descriptions
Verification results including code version, date, etc.
Numerical sensitivity studies
Feature coverage in verification

Below, we briefly describe the characteristics of each type of benchmark documentation (could be called artifacts or meta-data) associated with a code verification benchmarks. These artifacts take a number of concrete forms such as a written document, computer code, mathematical solution in document or software form, input files for executable codes, input to automatic computer analysis, output from software quality systems, among others.

Detailed technical description of the benchmark (report or paper): This can include a technical paper in a journal or conference proceeding describing the benchmark and its solution. Another form would be a report informal or formal from an institution providing the same information.
Analysis of the mathematics (report or paper): For any solution that is closed form, or requiring a semi-analytical solution, the mathematics must be described in detail. This can be included in the paper (report) discussed previously or in a separate document.
Computer analysis of solution (input file): If the mathematics or solution is accomplished using a computerized analysis, the program used and the input to the program should be included. Some sort of written documentation such as a manual for the software ideally accompanies this artifact.
Computer solution of the mathematical solution: The actual computerized solution of the mathematical problem should be included in whatever form the computerized solution takes. This should include any error analysis completed with this solution.
Computer implementation of the numerical solution: The analytical solution should be implemented in a computational form to allow the comparison with the numerical solution. This should include some sort of error analysis in the form of a report.
Derivation of the source term and software implementation or input: In the case of the method of manufactured solutions, the source term used to drive the numerical method must be derived through a well-defined numerical procedure. This should be documented through a document, and numerical tools used for the derivation and implementation.
Computer implementation of the source term (manufactured solution): The source term should be included in a form amenable to direct use in a computer code. The language for the computer code should be clearly defined as well as the compiler and computer system used.
Grids for numerical solution: If a solution is computed using another simulation code all relevant details on the numerical grid(s) used must be included. This could be direct grid files, or input files to well-defined grid generation software.
Convergence and error estimation of numerical solution: The numerical solution must include a convergence study and error estimate. These should be detailed in an appropriately peer-reviewed document.
Uncertainty and sensitivity study of numerical solution: The various modeling options in the code used to provide the numerical solution must be examined vis-a-vis the uncertainty and sensitivity of the solution to these choices. This study should be used to justify the methodology used for the baseline solution.
Description and analysis of computational methods: The methods used by the code used for the baseline solution must be completely described and analyzed. This can take the form of a complete bibliography of readily available literature
Numerical analysis theory associated with convergence: The nature of the convergence and the magnitude of error in the numerical solution must be described and demonstrated. This can take the form of a complete bibliography of readily available literature.
Code description/manuals: The code manual and complete description must be included with the analysis and description.
Input files for benchmarks and auxiliary software: The input file used to produce the solution must be included. Any auxiliary software used to produce or analyze the solution must be full described or included.
Unusual boundary conditions (inflow, piston, outflow, Robin, symmetry, …): Should the benchmark require unusual or involved boundary or initial conditions, these must be described in additional detail including the nature of implementation.
Physics restrictions (boundary layer theory, inviscid, parabolized Navier-Stokes, …): If the solution requires the solution of a reduced or restricted set of equations, this must be fully described. Examples are boundary layer theory, truly inviscid flow, or various asymptotic limits.
Software quality documents: Of non-commercial software used to produce solutions, the software quality pedigree should be clearly established by documenting the software quality and steps taken to assure the maintenance of the quality.
Scripts and auxiliary software for verification: Auxiliary software or scripts used to determine the verification or compute error estimates for a software used to produce solution should be included.
Source code: If possible the actual source code for the software along with instructions for producing an executable (makefile, scripts) should be included with all other documentation.
A full mathematical or computational description of metrics used in error analysis and evaluation of solution implementation or numerical solution.
Verification results including code version, date, and other identifying characteristics: The verification basis for the code used to produce the baseline solution must be included. This includes any documentation of verification, peer-review, code version, date completed and error estimates.
Feature coverage in verification: The code features covered by verification benchmarks must be documented. Any gaps where the feature used for the baseline solution are not verified must be explicitly documented.

Below are the necessary data requirements for each category of benchmark, again arranged in order of increasing level of documentation required. For completeness each data type would expected to be available to describe a benchmark of a given type.

Common elements for all types of benchmarks (it is notable that the use of proper verification using an analytical solution results in the most compact set of requirements for data, manufactured solutions also).

Paper or report
Mathematical analysis
Computerized solution and input
Error and uncertainty analysis
Computer implementation of the evaluation of the solution
Restrictions
Boundary or initial conditions

Closed form analytical solution

Paper or report
Mathematical analysis
Computerized solution and input
Error and uncertainty analysis
Computer implementation of the evaluation of the solution
Restrictions
Boundary or initial conditions

Manufactured Solution

Paper or report
Mathematical analysis
Computational solution and input
Error and uncertainty analysis
Computer implementation of the evaluation of the solution
Derivation and implementation of the source term
Restrictions
Boundary or initial conditions

Numerical solution with analytical solution
Series solution, Nonlinear algebraic solution, Nonlinear ODE solution

Paper or report
Mathematical analysis
Computerized solution and input
Error and uncertainty analysis
Computer implementation of the evaluation of the solution
Input files
Source code
Source code SQA
Method description and manual
Restrictions
Boundary or initial conditions

Highly accurate numerical solution (not analytical), numerical benchmarks or code-to-code comparisons.

Paper or report
Mathematical analysis
Computational solution and input
Error and uncertainty analysis for the solution
Computer implementation of the evaluation of the solution
Input files
Grids
Source code
Source code SQA
Method description and manual
Method analysis
Method verification analysis and coverage
Restrictions
Boundary or initial conditions

The use of direct numerical simulation requires a similar or even higher level of documentation than analytical solutions. This coincides with the discussion of the last type of verification benchmark where a complex numerical method with significant approximations is utilized to produce the solution. As a numerically computed benchmark, the burden of proof is much larger. Code verification is best served by exact analytical solutions because of the relative ease in assuring benchmark solution accuracy. Nonetheless, it remains a common practice due to its inherent simplicity. It also appeals to those who have a vested interest in the solutions produced by a certain computer code. The credibility of the comparison is predicated on the credibility of the code producing the “benchmark” used as the surrogate for truth. Therefore the documentation of the benchmark must provide the basis for the credibility.

The use of DNS as a surrogate for experimental data has received significant attention. This practice violates the fundamental definition of validation we have adopted because no observation of the physical world is used to define the data. This practice also raises other difficulties, which we will elaborate upon. First the DNS code itself requires that the verification basis further augmented by a validation basis for its application. This includes all the activities that would define a validation study including experimental uncertainty analysis numerical and physical equation based error analysis. Most commonly, the DNS serves to provide validation, but the DNS contains approximation errors that must be estimated as part of the “error bars” for the data. Furthermore, the code must have documented credibility beyond the details of the calculation used as data. This level of documentation again takes the form of the last form of verification benchmark introduced above because of the nature of DNS codes. For this reason we include DNS as a member of this family of benchmarks.

There are two ways to do great mathematics. The first is to be smarter than everybody else. The second way is to be stupider than everybody else — but persistent.

― Raoul Bott

Banks, Jeffrey W., T. Aslam, and William J. Rider. “On sub-linear convergence for linearly degenerate waves in capturing schemes.” Journal of Computational Physics 227, no. 14 (2008): 6985-7002.

Greenough, J. A., and W. J. Rider. “A quantitative comparison of numerical methods for the compressible Euler equations: fifth-order WENO and piecewise-linear Godunov.” Journal of Computational Physics 196, no. 1 (2004): 259-281.

Kamm, James R., Jerry S. Brock, Scott T. Brandon, David L. Cotrell, Bryan Johnson, Patrick Knupp, W. Rider, T. Trucano, and V. Gregory Weirs. Enhanced verification test suite for physics simulation codes. No. LLNL-TR-411291. Lawrence Livermore National Laboratory (LLNL), Livermore, CA, 2008.

Rider, J., James R. Kamm, and V. Gregory Weirs. “Verification, Validation and Uncertainty Quantification Workflow in CASL.” Albuquerque, NM: Sandia National Laboratories (2010).

Rider, William J., James R. Kamm, and V. Gregory Weirs. “Procedures for Calculation Verification.” Simulation Credibility (2016): 31.

How’s? What’s? Why’s?

10 Monday Jul 2017

Posted by Bill Rider in Uncategorized

≈ Leave a comment

He who has a why to live for can bear almost any how.
― Friedrich Nietzsche

At work we often justify the research we do through declaring that it is mission-relevant, or mission-focused. The work is automatically important and necessary if it supports our mission. Defining the mission is then essential to this conversation. Currently in my work, the discussion of what the mission is focuses on high performance computing. The pregnant question is whether my work’s mission is high performance computing?

I unilaterally reject this as a mission.

High performance computing is a “how” and so is “modeling and simulation” for that matter. Both things are tools to conduct science and engineering specialized to a purpose. Neither is a viable mission or reason in and of itself. Missions are better defined as “what’s” like nuclear weapons, economic competitiveness or scientific investigation. The high performance computing is how modeling and simulation is done, which is how aspects of nuclear weapons work or science or industrial work is done, but certainly not all of any of these. We still haven’t gotten to why we do these things. Why we fund high performance computing for modeling and simulation to support the nuclear weapons stockpile is an intricate question worth some further exploration.

A knee jerk response is “National Security,” which avoids a deeper discussion. The defense of a Nation State is associated with ability of the citizens of that Nation to achieve a degree of access to resources that raise their access to a good life. With more resources the citizens can aspire toward a better, easier more fulfilled life. In essence the security of a Nation can allow people to exist higher on Maslow’s hierarchy needs. In the United States this is commonly expressed as “freedom”. Freedom is a rather superficial thing when used as a slogan. The needs of the citizens begin with having food and shelter than allow them to aspire toward a sense of personal safety. Societal safety is one means of achieving this (not that safety and security are pretty low on the hierarchy). With these in hand, the sense of community can be pursued and then sense of an esteemed self. Finally we get to the peak and the ability to pursue ones full personal potential.

At the lowest part of the hierarchy is subsistence, the need for basic resources to survive. If one exists at this level, life isn’t very good, but its achievement is necessary for a better life. Gradually one moves up the hierarchy requiring greater access to resources and ease of maintaining the lower positions on the hierarchy. A vibrant National Security should allow this to happen, the richer a Nation becomes the higher on the hierarchy of needs its citizens reside. It is with some recognition of irony that my efforts and the Nation is stuck at such a low level on the hierarchy. Efforts toward bolstering the community the Nation forms seem to be too difficult to achieve today. We seem to be regressing from being a community or achieving personal fulfillment. We are stuck trying to be safe and secure. The question is whether those in the Nation can effectively provide the basis for existing high on the hierarchy of needs without being there themselves?

My observation about my work is that the people doing the work to support National Security are moving to lower and lower levels of the hierarchy by being isolated from the “why’s” of their work, and pushed into a subsistence existence focused on the “how’s”. Increasingly the work is even divorced from the “what’s” and the “why” is never even considered. As a result people simply do what they are told without considering what it is for, or why they are doing it. The result is a decline in the quality and applicability of the foundational work, which should adapt to the needs of its use and inspired by the underlying reasons. This issue is rampant in high performance computing where its utility for modeling and simulation is intellectually threadbare, and those working in computing barely consider what any of their work will be used for.

We are seeing our scientific community pushed to ever lower rungs Maslow’s pyramid. Part of this is the pervasive distrust of experts and education in the United States and perhaps the entirety of the West. These problems are harbingers of decline and hardly support the expansion and vibrancy of democracy or freedom.

Good Validation Practices are our Greatest Opportunity to Advance Modeling and Simulation

07 Friday Jul 2017

Posted by Bill Rider in Uncategorized

≈ 3 Comments

It doesn’t matter how beautiful your theory is … If it doesn’t agree with experiment, it’s wrong.

― Richard Feynman

It is an oft-stated maxim that we should grasp the lowest hanging fruit. In real life this often is hidden in plain sight with modeling and simulation being a prime example in my mind. Even a casual observer could see that the emphasis today is focused on computing speed and power as the path to the future. At the same time one can also see that the push for faster computers is foolhardy and hardly comes at an opportune time. Moore’s law is dead, and may be dead at all scales of computation. It may be the highest hanging fruit pursued at great cost while lower hanging fruits rots away without serious attention, or even conscious neglect. Perhaps nothing typifies this issue more than the state of validation in modeling and simulation.

Validation can be simply stated, but is immensely complex to do correctly. Simply put, validation is the comparison of observations with modeling and simulation results with the intent of understanding the fitness of the model for its intended purpose. More correctly, it is an assessment of modeling correctness, which demands observational data to ground the comparison in reality. It involves deep understanding of experimental and observational science including inherent error and uncertainty. It also involves equally deep understanding of errors and uncertainty of the model. It must be couched in the proper context philosophically including understanding what a model is. Each of these endeavors is in itself a complex and difficult professional activity, and validation is the synthesis of all of it. Being so complex and difficult it is rarely done correctly, and its value is grossly underappreciated. A large part of the reason for this state of affairs is the tendency to completely accept genuinely shoddy validation. I used to give a talk on the validation horrors in the published literature and finding targets for critique basically comes down to looking at almost any paper that does validation. The hard part is finding examples where the validation is done well.

The-most-powerful-Exascale-Computer

One of the greatest tenets of modeling is the quote by George Box, “all models are wrong, but some are useful.” We have failed to recognize one of the most important, but poorly appreciate maxims of modeling and simulation and corollary to Box’s observation. It is that no amount of computer speed, algorithmic efficiency or accuracy of approximation can make a bad model better. If the model is wrong, solving it faster or more accurately or more efficiently will not improve it. A question that should immediately come to mind “what is useful?” “what is a bad?” and “what is better?” In a deep sense both of these questions are completely answered by a comprehensive validation assessment of the simulation of a model. One needs to define what is bad and what is better. Both concepts depend deeply upon deciding what one wants from a model. What is its point and purpose, and most likely what question is it designed to answer. A question to start things off first understands, “what is a model?”

“What is a model?”

A model is virtually everything associated with a simulation including the code itself, the input to the code, the computer used for the computation, and the analysis of the results. Together all these elements comprise the model. At the core of the model and the code are the theoretical equations being used simulating the real World? More often than not, this is a system of differential equations or something more complex (like integral differential equations for example). These equations are then solved using methods, approximations and algorithms all of which leave their imprint on the results. Putting all of this involves creating a computer code, creating a discrete description of the World and computing that result. Each of these steps constitutes a part of the model. Once the computation has been completed, the results need to analyze and results drawn out of the mountain of numbers produced by the computer. All of these comprise the model we are validating. To separate one thing from another requires good disciplined work and lots of rigor. Usually this discipline is lacking and rigor is replaced by assumptions and slothful practices. In very many cases we are watching willful ignorance in action, or simple negligence. We know how to do validation; we simply don’t demand that people practice it. People are often comforted not knowing and don’t want to actually understand the depth of their structural ignorance.

Science is not about making predictions or performing experiments. Science is about explaining.

― Bill Gaede

Observing and understanding are two different things.

― Mary E. Pearson

vyxvbzwx To conduct a validation assessment you need observations to compare to. This is an absolute necessity; if you have no observational data, you have no validation. Once the data is at hand, you need to understand how good it is. This means understanding how uncertain the data is. This uncertainty can come from three major aspects of the process: errors in measurement, errors in statistics, and errors in interpretation. In the order of how these were mentioned each of these categories become more difficult to assess and less common to actually be assessed in practice. Most commonly assessed is measurement error that is the uncertainty of the value of a measured quantity. This is a function of the measurement technology or the inference of the quantity from other data. The second aspect is associated with the statistical nature of the measurement. Is the observation or experiment repeatable? If it is not how much might the measured value differ due to changes in the system being observed? How typical are the measured values? In many cases this issue is ignored in a willfully ignorant manner. Finally, the hardest part of observational bias often defined as answering the question, “how do we know that we a measuring what we think we are?” Is there something systematic in our observed system that we have not accounted for that might be changing our observations. This may come from some sort of problem in calibrating measurements, or looking at the observed system in a manner that is inconsistent. These all lead to potential bias and distortion of the measurements.

images The intrinsic benefit of this approach is a systematic investigation of the ability of the model to produce the features of reality. Ultimately the model needs to produce the features of reality that we care about, and can measure. This combination is good to balance in the process of validation, the ability to produce the reality necessary to conduct engineering and science, but also general observations. A really good confidence builder is the ability of model to produce proper results on things that we care as well as those don’t care about. One of the core issues is the high probability that many of the things we care about in a model cannot be observed, and the model acts as an inference device for science. In this case the observations act to provide confidence that the model’s inferences can be trusted. One of the keys to the whole enterprise is understanding the uncertainty intrinsic to these inferences, and good validation provides essential information for this.

One of the things few people recognize is the inability of other means to provide remediation from problems with the model. If a model is flawed there is no amount of computer power that can rectify its shortcomings. A computer of infinite speed would (should) only make the problems more apparent. This obvious outcome only becomes available with a complete, rigorous and focused validation of the model. Slipshod validation practices simply allow the wrong model to be propagated without necessary feedback. It is bad science plain and simple. No numerical method or algorithm in the code could provide relief either. The leadership in high performance computing is utterly oblivious to this. As a result almost no effort whatsoever is being put into validation, and models are being propagated forward without any thought regarding their validity. No serious effort exists to put the models to the test either. If our leadership is remotely competent this is an act of willful ignorance, i.e., negligence. While our models today are wonderful in many regards, they are far from perfect (remember what George Box said!). A well-structured scientific and engineering enterprise would make this evident, and employ means to improving them. These new models would open broad new vistas of utility in science and engineering. A lack of recognition of this opportunity makes modeling and simulation self-limiting in its impact.

A prime example where our modeling and simulation are deficient is reproducing the variability seen in the real World. In many cases the experimental practice is equally deficient. For most phenomena of genuine interest and challenge, events and engineered products the exact same response cannot be produced. There are variations in the response because of small differences in the system being studied coming from external conditions (boundary conditions) or the state of system (initial conditions), or simply a degree of heterogeneous character in the system itself. In many cases the degree of variation in response is very large and terribly important. In engineered systems this leads to the application of large and expensive safety factors along with the risk of disaster. This depends to some extent on the nature of the response be sought. The more localized the response, the greater the tendency to be variable, while global-integrated responses can be far more reliably reproduced.

Crays-Titan-Supercomputer Our scientific and engineering attention is being drawn increasingly to the local responses for significant events, and their importance is growing. These are often worst-case conditions that we strive to avoid. At the same time our models are completely ill suited to address these responses. Our models cannot effectively simulate these sorts of features. Our models are almost without exception focused on a mean-field model producing a model of the average system involving far more homogeneous properties and responses than seen in reality. As such the extremes in response are removed a priori. By the same token our observational and experimental practices are not arrayed to unveil this increasingly essential aspect of reality. The ability of modeling and simulation to impact the real World effectively suffers and its impact is limited by failing to progress.

…if you’re doing an experiment, you should report everything that you think might make it invalid—not only what you think is right about it: other causes that could possibly explain your results; and things you thought of that you’ve eliminated by some other experiment, and how they worked—to make sure the other fellow can tell they have been eliminated.

― Richard Feynman

incompetencedemotivator One of the greatest issues in validation is “negligible” errors and uncertainties. In many cases these errors are negligible by assertion and no evidence is given. A standing suggestion is that any negligible error or uncertainty be given a numerical value along with evidence for that value. If this cannot be done, the assertion is most likely to be specious, or at least poorly thought through. If you know it is small then you should know how small and why. It is more likely is that it is based on some combination of laziness and wishful thinking. In other cases this practice is an act of negligence, and worse yet it is simply willful ignorance on the part of practitioners. This is an equal opportunity issue for computational modeling and experiments. Often (almost always!) numerical errors are completely ignored in validation. The most brazen violators will simply assert without evidence that the errors are small or the calculated is converged without offering any evidence beyond authority.

The greatest enemy of knowledge is not ignorance, it is the illusion of knowledge.

― Daniel J. Boorstin

Similarly, in experiments measurements will be offered without any measurement error, and often no evidence along with an assertion that the error is too small to be concerned about. Experimental or observational results are also highly prone to ignore variability in outcomes and treat each case as a well-determined result even when the physics of the problem is strongly dependent on the details of the initial conditions (or the prevailing models strongly imply this!). Similar sins are committed with modeling uncertainties where an incomplete assessment is made of uncertainty, and no accounting is made of the incompleteness and its impact. To make matters worse other obvious sources of uncertainty are ignored. The result of these patterns of conduct is an almost universal under-estimate of uncertainty from both modeling and observations. This under-estimate results in modeling and simulation being applied in a manner that is non-conservative from a decision-making perspective.

The result of these rather sloppy practices is a severely limited capacity to properly offer an assessment of model validation. Using rather complete uncertainties can produce the sort of result needed to produce definitive results that offer feedback on modeling. If uncertainties can be driven small enough we can drive improvement in the underlying science and engineering. For example, very precise and well-controlled experiments with small uncertainties can produce evidence that models must be improved. Exceptionally small modeling uncertainty could produce a similar effect in pushing experiments. Too often the work is conducted with a strong confirmation bias that takes the possibility of model incorrectness off the table. The result is a stagnant situation where models are not improving and shoddy professional practice is accepted. All of this stems from a lack of understanding or priority for proper validation assessment.

Confidence is ignorance. If you’re feeling cocky, it’s because there’s something you don’t know.

― Eoin Colfer

A mature realization for scientists is that validation is never complete. Models are validated, not codes. The model is a broad set of simulation features, including the model equations, and the code, but also a huge swath of other things. The validation is simply an assessment of all those things. This assessment looks at whether the model and the data are consistent with each other given the uncertainties in each. This assessment is predicated on the completeness of the uncertainty estimation. In the grand scheme of things one wants drive the uncertainties down in either the model or the observations of reality. The big scientific endeavor is locating the source of error in the model; is it in how the model is solved? Or are the model equations flawed? A flawed theoretical model can be a major scientific result requiring a deep theoretical response. Repairing these flaws can open new doors of understanding and drive our knowledge forward in miraculous ways. We need to adopt practices that allow us to identify problems that new models are needed for. The current modeling and simulation practice removes this outcome as a possibility at the outset.

A man is responsible for his ignorance.

― Milan Kundera

Rider, William J. A Rogue’s Gallery of V&V Practice. No. SAND2009-4667C. Sandia National Laboratories (SNL-NM), Albuquerque, NM (United States), 2009.

Rider, William J. What Makes A Calculation Good? Or Bad?. No. SAND2011-7666C. Sandia National Laboratories (SNL-NM), Albuquerque, NM (United States), 2011.

Rider, William J. What is verification and validation (and what is not!)?. No. SAND2010-1954C. Sandia National Laboratories, 2010.

The Regularized Singularity

~ The Eyes of a citizen; the voice of the silent

Monthly Archives: July 2017

Question, Analyze, Understand and Create,… Repeat

The Foundations of Verification: Solution Verification

The Foundations of Verification: Code Verification

How’s? What’s? Why’s?

Good Validation Practices are our Greatest Opportunity to Advance Modeling and Simulation