tl;dr.

The practice of code verification has focused on finding bugs in codes. This is grounded in the proving that a code is correctly implementing a method. While this is useful and important, it does not inspire. Code verification can be used for far more. It can be the partner to method development and validation or application assessment. It can also provide expectations for code behavior and mesh requirements on applications. Together these steps can make code verification more relevant and inspiring. It can connect it to important scientific and engineering work pulling it away from computer science.

When you can measure what you are speaking about, and express it in numbers, you know something about it.

– Lord Kelvin

My Connection to Code Verification

Writing about code verification might seem like a scheme to reduce my already barren readership. All kidding aside, code verification is not the most compelling topic for most. This includes people making their living writing computational solvers. For me it is a topic of much greater gravity. While I am inspired by the topic, most people are not. The objective here is to widen its scope and importance. Critically, I have noticed the problems getting worse as code verification seems to fade from serious attention. This all points to a need for me to think about this topic deeply. It is time to consider a change to how code verification is talked about.

“If you can not measure it, you can not improve it.”

– Lord Kelvin

My starting point for thinking about code verification is to look at myself. Code verification is something I’ve been doing for more than 30 years. I did it before I knew it was called “code verification.” Originally, I did it to assist my development of improved methods in codes I worked on. I also used it to assure that my code was correct, but this was secondary. This work utilized test problems to measure the correctness and more importantly the quality of methods. As I continued to mature and grow in my scientific career I sought to enhance my craft. The key aspect of growth was utilizing verification to exactly measure method character and quality. It was through verification that I understood if a method passed muster.

“If failure is not an option, then neither is success.”

― Seth Godin

Eventually, I developed new problems to more acutely measure methods. I also developed problems to break methods and codes. When you break a method you help define its limitations. Over time I saw the power of code verification as I practiced it. This contrasted to how it was described by V&V experts. The huge advantage and utility of code verification I found in method development was absent. Code verification was relegated to correctness through code bug detection. In this mode code verification is a spectator to the real work of science. I know it can be so very much more.

“I have been struck again and again by how important measurement is to improving the human condition.”

– Bill Gates

The Problem with Code Verification

In the past year I’ve reviewed many different proposals in computational science. Almost all of them should be utilizing code verification integrally in their work. Almost all of them failed to do so. At best, code verification is given lip service because of proposal expectations. At worst it is completely ignored. The reason is that code verification does not set itself as a serious activity for scientific work. It is viewed as a trivial activity beneath mention in a research proposal. The fault lies with the V&V community’s narrative about it. (I’ve written before on the topic generally https://williamjrider.wordpress.com/2024/08/14/algorithms-are-the-best-way-to-improve-computing-power/)

“Program testing can be used to show the presence of bugs, but never to show their absence!”

― Edsger W. Dijkstra

Let’s take a look at the narrative chosen for code verification more closely. Code verification is discussed primarily as a manner to detect bugs in the code. The bugs are detected when the code does not act as a consistent solution of the governing equations in the manner desired. This comes when the exact solution to those governing equations does not match the order of accuracy designed for the method. This places code verification as part of software development and quality. This is definitely an important topic, but far from a captivating one. At the same time code verification is distanced from math, physics and aapplication space engineering. Thus, code verification does not feel like science.

This is the disconnect. To be focused upon in proposals and work code verification needs to be part of a scientific activity. It simply is not one right now. Of all the parts of V&V, it is the most distant from what the researcher cares about. More importantly, this is completely and utterly unnecessary. Code verification can be a much more holistic and integrated part of the scientific investigation. It can span all the way from software correctness to physics and application science. If the work involves development of better solution methodology, it can be the engine of measurement. Without measurement “better” cannot be determined and is left to bullshit and bluster.

“Change almost never fails because it’s too early. It almost always fails because it’s too late.”

― Seth Godin

What to do about it?

The way forward is to expand code verification to include activities that are more consequential. To constructively discuss the problem, the first thing to recognize that V&V is the scientific method for computational science. It is essential to have correct code. The software correctness and quality aspects of code verification remain important. If one is doing science with simulation, the errors made in simulation are more important. Code verification needs to contribute to error analysis and minimization. Another key part of simulation are choices about the methods used. Code verification can be harnessed to serve better methods. The key in this discussion is that the additional tasks are not discussed in what code verification is. This is an outright oversight.

Appreciate when things go awry. It makes for a better story to share later.

― Simon Sinek

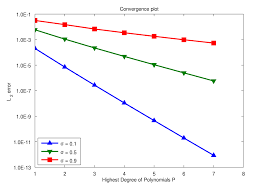
Let’s discuss each of these elements in turn. First we should get to some technical details of code verification practice. The fundamental tool in code verification is using exact solutions to determine the rate of convergence of a method in a code. The objective is to show the code implementation produces the theoretical order of accuracy. This is usually accomplished by computing errors on different meshes.

The order of accuracy comes from numerical analysis of the truncation errors of a method. It is usually takes the form of a power of the mesh size. For example a first order method the error is proportional to the mesh size. For a second order method the error depends on the square of the mesh size. This all follows from the analysis and has the error vanishing as the mesh size goes to zero (see Oberkampf and Roy 2010)

The grounding of code verification is found in the work of Peter Lax. He discovered the fundamental theorem of numerical analysis (Lax and Richtmyer 1956). This theorem says that a method is a convergent approximation of the partial differential equation if it is consistent and is stable. Stability comes from getting an answer that does not fall apart into numerical garbage. Practically speaking, stability is assumed when the code produces a credible answer to problems. The trick of consistency is that the method reproduces the differential equation plus an ordered remainder. Now the trick of verification is that you invert this and use a convergent sequences to infer consistency. This is a bit of a leap of faith.

“Look for what you notice but no one else sees.”

― Rick Rubin

The additional elements for verification

The most important aspect to add to code verification is stronger connection to validation. Numerical error is an important element in validation and application results. Currently code verification is divorced from validation. This makes it ignorable in the scientific enterprise. To connect better, the errors in verification work need to be used to understand mesh requirements for solution features. This means that the exact solutions used need to reflect true aspects of the validation problem.

Current verification practice pushes this activity into the background of validation. In doing “bug hunting” code verification, the method of manufactured solutions (MMS) is invaluable. The problem is that MMS solutions usually bear no resemblance to validation problems. For people concerned with real problems MMS problems have no interest, nor guidance for their solutions. Instead verification problems should be chosen that feature phenomena and structures like those validated. Then the error expectations and mesh requirements can be determined. Code verification can then be used as simple pre-simulation work before validation ready calculations are done. Ultimately this will require the development of new verification problems. This is deep physics and mathematical work. Today this sort of work is rarely done.

The next big change in code verification is connecting code verification more actively to method-algorithm research. Code verification can be used to measure the error of a method directly. Again this requires a focus on error instead of convergence rate. The convergence rate is still relevant and needs to be verified. At the same time methods with the same convergence rate can have greatly different error magnitudes. For more realistic problems the order of accuracy does not determine the error. It has been shown that low order methods can out perform higher order methods in terms of error (see Greenough and Rider 2005).

“There is no such thing as a perfect method. Methods always can be improved upon.”

–  Walter Daiber

In all aspects of developing a method code verification is useful. The base of making sure the implementation is correct remains. The additional aspect that I am suggesting is the ability to assess the method dynamically. This should be done on a wide range of problems biased toward application-validation inspired problems. In terms of making this activity supported by those doing science, the application-validation inspired problems are essential. This is also where code verification fails most miserably. The best example of this failure can be found in shock wave calculations.

“If you can’t measure it, you can’t change it.”

– Peter Drucker

Let’s take a brief digression to how verification currently is practiced in shock wave methods. Invariably the only time you see detailed quantitative error analysis is on a smooth differentable prroblem. This problem has no shocks and can be used to show a method has the “right” order of accuracy. This is expected and common. The only value is the demonstration that a nth order method is indeed nth order. It has no practical value for the use of the codes.

“Measure what is measurable, and make measurable what is not so.”

– Galileo Galilei

Once a problem has a shock in it, the error analysis and convergence rates disappear from the work. Problems are only compared in the “eyeball norm” to an analytic or high resolution solution. The reason for this is that the convergence rate with a discontinuity is one or less. The reality being ignored is that error can be very different (see the paper by Greenough and Rider 2005). When I tried to publish a paper that used errors and convergence rates to assess the method with shock, the material needed to be deleted. As the associate editor told me bluntly, “if you want to publish this paper get that shit out of the paper!” (see Rider, Greenough and Kamm 2007)

Experts are the ones who think they know everything. Geniuses are the ones who know they don’t

― Simon Sinek

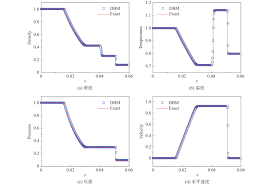
Why is this true? Part of the reason is the belief that the accuracy does not matter any longer. The failure is to recognize how different the errors can be. This has become accepted practice. Gary Sod introduced the canonical shock tube problem that bears his name. Sod’s shock tube has been called the “Hello World” problem for shock waves. In Sod’s 1978 paper the run time of different methods was given, but errors were never shown. The comparison with analytical solution to the problem was qualitative, the eyeball norm. Subsequently, this became the accepted practice. Almost no one ever computes the error or convergence rate for Sod’s problem or any other shocked problem.

“One accurate measurement is worth a thousand expert opinions.”

– Grace Hopper

As I have written and shown recently this is a rather profound oversight. The importance of the error level for a given method is actually far greater if the convergence rate is low. The lower the convergence rate, the more important the error is. Thus we are not displaying the errors created by methods in the conditions where it matters the most. This is a huge flaw in the accepted practice and a massive gap in the practice of code verification. It is something that needs to change.

“The Cul-de-Sac ( French for “dead end” ) … is a situation where you work and work and work and nothing much changes”

― Seth Godin

My own practical experience speaks volumes about the need for this. Virtually every practical application problem I have solved or been associated with converges at low order (first order or less). The accuracy of the methods under these circumstances mean the most to the practical use of simulation. Because of how we currently practice code verification applied work is not impacted. There is a tremendous opportunity to improve calculations using code verification. As I noted a couple of blog posts ago, the lower the convergence rate, the more important the error is (https://williamjrider.wordpress.com/2024/08/14/algorithms-are-the-best-way-to-improve-computing-power/). A low error method can end up being orders of magnitude more efficient. This can only be achieved if the way code verification is done and its scope increase. This will also draw it together with the full set of application and validation work.

More related content (https://williamjrider.wordpress.com/2017/12/01/is-the-code-part-of-the-model/, https://williamjrider.wordpress.com/2017/10/27/verification-and-numerical-analysis-are-inseparable/, https://williamjrider.wordpress.com/2015/01/29/verification-youre-doing-it-wrong/, https://williamjrider.wordpress.com/2014/05/14/important-details-about-verification-that-most-people-miss/,

https://williamjrider.wordpress.com/2014/01/31/whats-wrong-with-how-we-talk-about-verification/

“If it scares you, it might be a good thing to try.”

– Seth Godin

Roache, Patrick J. Verification and validation in computational science and engineering. Vol. 895. Albuquerque, NM: Hermosa, 1998.

Oberkampf, William L., and Christopher J. Roy. Verification and validation in scientific computing. Cambridge university press, 2010.

Lax, Peter D., and Robert D. Richtmyer. “Survey of the stability of linear finite difference equations.” In Selected Papers Volume I, pp. 125-151. Springer, New York, NY, 2005.

Roache, Patrick J. “Code verification by the method of manufactured solutions.” J. Fluids Eng. 124, no. 1 (2002): 4-10.

Greenough, J. A., and W. J. Rider. “A quantitative comparison of numerical methods for the compressible Euler equations: fifth-order WENO and piecewise-linear Godunov.” Journal of Computational Physics 196, no. 1 (2004): 259-281.

Rider, William J., Jeffrey A. Greenough, and James R. Kamm. “Accurate monotonicity-and extrema-preserving methods through adaptive nonlinear hybridizations.” Journal of Computational Physics 225, no. 2 (2007): 1827-1848.

Sod, Gary A. “A survey of several finite difference methods for systems of nonlinear hyperbolic conservation laws.” Journal of computational physics 27, no. 1 (1978): 1-31.

tl;dr; Algorithms shape our world today. When a new algorithm is created it can transform a computational landscape. These changes happen in enormous leaps that take us by surprise. The latest changes in the artificial intelligence are the result of such a breakthrough. It is unlikely to be followed by another breakthrough soon reducing the seeming pace of change. For this reason the threats of doom and vast wealth are overblown. If we want more progress it is essential to understand how such breakthroughs happen and their limits.

“The purpose of computing is insight, not numbers.”

– Richard Hamming

We live in the age of the algorithm. In the past ten years this has leapt to the front of mind with social media and the online world. It has actually been true ever since the computer took hold of society. This began in the 1940’s with the first serious computers, and numerical mathematics. A new improved algorithm always drives the use of the computer forward as much as hardware. What people do not realize is that the improvements that get noticed are practically quantum in change. These algorithms get our attention.

“I am worried that algorithms are getting too prominent in the world. It started out that computer scientists were worried nobody was listening to us. Now I’m worried that too many people are listening.”

– Donald Knuth

Now that the internet has become central to our lives we need to understand this. One reason is understanding how algorithms create value for business and stock market valuations. How these sorts of advances fool people on the pace of change? We should also know how this breakthroughs are made. We need to understand how likely we are to see progress? How can we create an environment where advances are possible? How the way we fund and manage work actually destroys the ability to continue progress?

“You can harvest any data that you want, on anybody. You can infer any data that you like, and you can use it to manipulate them in any way that you choose. And you can roll out an algorithm that genuinely makes massive differences to people’s lives, both good and bad, without any checks and balances.”

– Hannah Fry

Two examples come to mind in recent year to illustrate these points. The first is the Google search algorithm, pagerank. The second is the transformer, which elevated large language models to the forefront of the public’s mind in the last two years. What both of these algorithms illustrate clearly is the pattern for algorithmic improvement. A quantum leap in performance and behavior followed by incremental changes. These incremental changes are basically fine tuning and optimization. They are welcome, but do not change the World. The key is realizing the impact of the quantum leap from an algorithm and putting it into proper perspective.

Google is an archetype

Google transformed search and the internet and ushered algorithms into the public eye. Finding things online used to be torture as early services tried to produce a “phone book” for the internet. I used Alta Vista, but Yahoo was another example. Then Google appeared and we never went back. Once you used Google the old indexes of the internet were done. It was like walking through a door. You shut the door and never looked back. This algorithm turned the company Google into a verb, household name and one of the most powerful forces on Earth. Behind it was an algorithm that blended graph theory and linear algebra into an engine of discovery. Today’s online world and its software are built on the foundation of Google.

“The Google algorithm was a significant development. I’ve had thank-you emails from people whose lives have been saved by information on a medical website or who have found the love of their life on a dating website.”

– Tim Berners-Lee

Google changed the internet introduced search and demonstrated the power of information. All of a sudden information was unveiled and shown to be power. Google unleashed the internet into a transformative engine for business, but society as well. The online world we know today owes its existence to Google. We need to acknowledge that Google today is a shadow of the algorithm of the past. Google has become a predatory monopoly and the epitome of “enshitification” of the internet. This is the process of getting worse over time. This is because Google is searching for profits over performance. Instead of giving us the best results they are selling spaces for money. This process is repeated across the internet undermining the power of the algorithms that created it.

“In comparison, Google is brilliant because it uses an algorithm that ranks Web pages by the number of links to them, with those links themselves valued by the number of links to their page of origin.”

– Michael Shermer

The Transformer and LLMs

The next glorious example of algorithmic power comes from Google (Brain) with the Transformer. Invented at Google in 2017 this algorithm has changed the world again. With a few tweaks and practical implementations OpenAI unleashed ChatGPT. This was a large language model (LLM) that ingested large swaths of the internet to teach it. The LLM can then produce results that were absolutely awe-inspiring. This was especially in comparison to what came before where suddenly the LLM could produce almost human like responses. Granted this is true if that human was a corporate dolt. Try to get ChatGPT to talk like a real fucking person! (just proved a person wrote this!)

“An algorithm must be seen to be believed.”

– Donald Knuth

These results were great even after OpenAI lobodomized ChatGPT with reinforcement learning that kept it from being politically incorrect. The LLM’s won’t curse or say racist or sexist stuff either. In the process the LLM becomes as lame as a conversation with your dullest coworker. The unrestrained ChatGPT was almost human in creativity, but also prone to sexist, racist and hate speech (like people). It is amazing to know how much creativity was sacrificed to make it corporately acceptable. It is worth thinking about and how this reflects on people. Does the wonder of creativity depend upon accepting our flaws?

Under the covers in the implementation of the foundation models at the core of ChatGPT is the transformer. The transformer has a couple of key elements. One if the ability to devour data in huge chunks perfectly fitting for modern GPU chips. This has allowed far more data to be used and transformed NVIDIA into a mulit-trillion dollar company overnight. This efficiency is only one of the two bits of magic. The real magic is the attention mechanism. This is what the LLM takes as instructions for its results. The transformer allows longer more complex instructions to be given. It also allows multiple instructions to guide its output. The attention mechanism has led to fundamentally different behavior from the LLMs. Together these elements demonstrate the power of algorithms.

“Science is what we understand well enough to explain to a computer. Art is everything else we do.”

– Donald Knuth

The real key to LLMs is NOT the computing available. A lot of capable computing helps and makes it easier. The real key to the huge leap in performance is the attention mechanism that changed the algorithm. This produced the qualitative change in how LLMs functioned. This produced the sort of results that made the difference. It was not the computers; it was the algorithms!

The world collectively lost their shit when ChatGPT went live. People everywhere freaked the fuck out! As noted above the impact could have easily been more profound without the restraint offered by reinforcement learning. Nonetheless feelings were unleashed that felt like we were on the cusp of exponential change. We are not. The reason why we are not is something key about the change. The real difference with these new LLMs was all predicated on the transformer algorithm’s character. Unless the breakthroughs of the transformer are repeated with new ideas, the exponential growth will not happen. Another change will happen, but it is not likely for a number of years from now.

A look at the history of computational science unveils that such changes happen more slowly. One cannot count on these algorithmic breakthroughs. They happen episodically with sudden leaps followed by periods of fallow growth. The fallow periods are optimization of the breakthrough and incremental change. As 2024 plays out I have become convinced that LLMs are like this. There will be no exponential growth into general AI that people fear. The transformer was the breakthrough and without another breakthrough we are on a pleateau of performance. Nonetheless like Google, ChatGPT was a world changing algorithm. Until a new algorithm is discovered, we will be on a slow path to change.

“So my favorite online dating website is OkCupid, not least because it was started by a group of mathematicians.”

– Hannah Fry

Computational Science and Quantum Leaps from Algorithms

To examine what this sort of algorithmic growth in performance we can look at examples from classical comptuational science. Linear algebra is an archetype of this sort of growth. Over a span of years from 1947 to 1985, the algorithmic performance matched the performance gains from hardware. This meant that Moore’s law for hardware was amplified by better algorithms. Moore’s law is the result of multiple technologies working together to create the exponential growth.

In the 1940’s linear algebra worked using dense matrix algorithms that scaled cubically with problem size. As it turned out most computational science applications were sparse structured matrices. These could be solved more efficiently with quadratic scaling. This was a huge difference. For a system with 1000 equations this is the difference of a million instead of a billion in terms of the work done and storage taken on the computer. Further advances happened with Krylov algorithms and ultimately multigrid where the scaling is linear (1000 in the above example). These are all huge speedups and advances. A key point is that the changes above occurred over the span of 40 years.

The nature of these changes is quantum in nature where the performance of the new algorithm leaps orders of magnitude. The new algorithm allows new problems to be solved and is efficient in ways the former algorithm is incapable of. This is exactly like what happened with the transformer. In between these advances the new algorithm is optimized and gets better. It does not change the fundamental performance. Nothing amazing happens until something is introduced that acts fundamentally differently. This is why there is a giant AI bubble. Unless another algorithmic advance is made, the LLM world will not change dramatically. The power and fears around AI is overblown. People do not understand that this moment is largely algorithmically driven.

These sorts of leaps in performance are not limited to linear algebra. In optimization a 1988 study showed a 43,000,000 times improvement in performance over a 15 year period. Of this improvement 1000 was due to computer improvements, but 43,000 was due to better algorithms. Another example is the profound change in hydrodynamic algorithms based on transport methods. The introduction of “limiters” in the early 1970’s allowed second-order methods to be used for the most difficult problems. Before the limiters the second-order methods produced oscillations that resulted in unphysical results. The difference was transformative. I have recently shown that the leap in performance is about a factor of 50 in three dimensions. Moreover the results also compare to the basic physical laws in ways the first-order methods cannot produce.

How do algorithms leap ahead?

“This is the real secret of life — to be completely engaged with what you are doing in the here and now. And instead of calling it work, realize it is play.” ― Alan Watts

Where do these algorithm breakthroughs come from? Some come out of pure inspiration where someone sees an entirely different way to solve a problem. Others come through the long slog through seeking efficiency. The deep analysis yields observations that are profound and lead to better approaches. Many are pure inspiration coming out of giving people the space to operate in a playful space. This playful space is largely absent in the modern business or government world. To play is to fail and to fail is to learn. Today we have everything planned and everyone should know that breakthroughs are not planned. We cannot play; we cannot fail; we cannot learn; breakthroughs are impossible.

“Our brains are built to benefit from play no matter what our age.”

– Theresa A. Kestly

The problems with algorithm advancements are everywhere in today’s environment. Lack of fundamental trust leads to constrained planning and lack of risk taking. Worse yet, failure is not allowed as the essential engine of learning and discovery. This sort of attitude is pervasive in the government and corporate system. Basic and applied research is both lacking funding and that funding is not free to go after problems.

In the corporate environment the breakthroughs often do not benefit the company where things are discovered. The transformer was discovered by Google (Brain), but the LLM breakthrough was made by OpenAI. Its greatest beneficiary is Google’s rival microsoft. A more natural way to harness the power of innovation is the government funding. There laboratories and universities can produce work that is in the public domain. At the same time the public domain is harmed by various information hiding policies and lack of transparency. We are not organized for success at these things as a society. We have destroyed most of the engines of innovation. Until these engines are restarted we will live in a fallow time.

“There is no innovation and creativity without failure. Period.”

― Brene Brown

I see this clearly at work. There we argue about whether to keep using 30, 40 and 50 year old algorithms rather than invest in the state of the art. They then convince themselves that it is good because their customers like the code. The code is modern because it is written in C++ instead of Fortran. The results feel good simply because they use the most modern computing hardware. Our “leadership” does not realize that this approach is getting substandard return on investment. If the algorithms were advancing the results would be vastly improved. Yet, there is little or no appetite to develop new algorithms or invest in research in finding them. This sort of research is too failure prone to fund.

“Good scientists will fight the system rather than learn to work with the system.”

– Richard Hamming

Page, Lawrence. The PageRank citation ranking: Bringing order to the web. Technical Report, 1999.

Vaswani, A. “Attention is all you need.” Advances in Neural Information Processing Systems (2017).Vaswani, A. “Attention is all you need.” Advances in Neural Information Processing Systems (2017).

Margolin, Len G., and William J. Rider. “A rationale for implicit turbulence modelling.” International Journal for Numerical Methods in Fluids 39, no. 9 (2002): 821-841.

Boris, Jay P., and David L. Book. “Flux-corrected transport. I. SHASTA, a fluid transport algorithm that works.” Journal of computational physics 11, no. 1 (1973): 38-69.

“They who can give up essential liberty to obtain a little temporary safety deserve neither liberty nor safety.”

― Benjamin Franklin,

The Trigger

The other day I headed into work for a face to face meeting. The meeting was an hour long. It was interesting and thought provoking. It also showed the utter disregard for the cost of actions in two ways. This meeting would cost me far more than an hour due to outright stupidity and lack of proper consideration. This sort of stupidity is rampant accross society today. It is destroying productivity, research and threatening our Nation’s security..

After the meeting I immediately got caught in a traffic jam trying to leave the Air Force base where my Lab is. This happens all too frequently and is maddening. The traffic was jammed up for more than an hour. It was also lunch hour, so more people than usual were on the road. It was a Friday, which mitigated some of the hassle since so many people work from home or don’t work Friday.

Why did this happen?

I heard from a friend that a motorcycle had run the security checks at the gates. This prompted the guards to institute a complete lockdown. This is the safest and most secure thing to do. Can’t take a risk, right? This is done without a thought about the costs. The thousands of people working on the base are frozen in place. As I’ve learned the costs of my time at work are rather extreme, about $350/hour. So if a 1000 people like me are put out for an hour this comes to $350,000. If it is 2000 people this is $700,000.

Is this worth the expense? No.

A rational response would be for the guards to chase the interloper down and arrest them. There is no reason to close the gates down. Surely they do so out of caution, extreme caution, that permiates society today. This caution always operates on the view that no cost be considered if safety or security is at risk. This attitude is absolutely irrational. It exacts costs from society at large that actually harm safety and security in the long run. It gets to the core of why we can’t accomplish great things today.

We choose the short term appearance of safety and security. This choice is destroying our long term safety and security as I will describe next.

“You tell them – you tell them there’s a cost…..Every decision we make in life, there’s always a cost.”

― Brad Meltzer,

It is everywhere one looks

If one looks around we see a lack of progress everywhere. We can’t build anything. Public works projects take forever (the big dig in Boston, or high speed rail). Government projects are all over cost and over time. Examples abound such as the F-35. Almost across the board our essential weapon’s systems are over cost and behind schedule. Under the covers the problem is prioritization of safety and security without thought to benefit compared with cost. For me the example of what my time costs is exhibit A. That cost is driven by out of control safety and security culture.

In my own life I am confronted with lots of deep security concerns that revolve around outlandish scenarios. The scenarios are plausible, but unlikely. The security people are granted carte blanche to take mitigations for the possible impacts. The cost on time and productivity are never considered. The programs funding research and useful work simply eat the costs. Worse yet, it would seem that safety and security professionals are actually rewarded for suggesting concerns. Their recommended mitigations are never put to the test of considering the cost for the benefit gained.

We might take the recent guidance federally regarding medical devices as an archetypical example. Medical devices are becoming increasingly complex and integrating new technology. A good example is a pacemaker that has bluetooth built in. The bluetooth increases the safety and benefit for the patient (my dad has one). The device can be checked often and remotely to monitor the patient and the health of the device. Yet the paranoia about bluetooth makes this a security concern. Another great example are bluetooth enabled hearing aids, which improve life for the hard of hearing.

What person in their right mind would accept a worse pacemaker simply to satisfy outlandish security concerns? Moreover, why would an employer ask someone to do this? This is the height of absurdity. You are either demanding someone risk their health or removing them from the workforce. Frankly I’m disgusted by this choice being imposed on someone. This is an absurdly low risk threat inducing a profoundly high consequence effect. Yes, something could happen possibly, but it is fantastically unlikely. It is not worth the cost of losing the efforts of the professionals removed from the workforce.

Much of this insanity calls back to the issues of trust discussed in the last post.

“As we care about more of humanity, we’re apt to mistake the harms around us for signs of how low the world has sunk rather than how high our standards have risen.”

― Steven Pinker

The TSA is exhibit 1

The lack of cost benefit considerations is perhaps most clear with the TSA’s practices. We have a situation where some asshole tries to light his shoes on fire 20 years ago on a plane and we still waste time over it. Richard Reid, who was an idiot, tried to blow up a plane by creating a shoe bomb. A fantastically stupid plot that got him imprisoned for life. In reaction people have to take off their shoes at security as well as limiting our fluid containers to 100 ml. We keep on doing this more than 20 years later with no end in sight. The cost of these measures on society is huge while the benefit is fleeting and highly questionable.

Let’s look at the cost more closely. For me, if I take 10 trips a year the extra time for these measures is perhaps 10 minutes each way. This tallies up to 3 extra hours a year. Now multiply this by 100 million people, and my $350 per hour rate and you get to $100 billion. This is undoubtably an over estimate, but it is still a huge cost nonetheless.

The time penalty is unambiguous. 300 million hours a year comes easily to 420 human life times. We habe been doing this for 20 years, so we are rapidly coming up on wasting 10,000 human lifetimes on this moronic safety measure. This along with what is likely more than a trillion dollars in lost productivity. All of this is because we can’t manage to examine the cost versus the benefit of this measure. It is also a perfect over-reaction to the act of one complete idiot by more idiots who weaponize safety and security.

We constantly hear this din of the bullshit that safety and security can be perfect with zero incidents. What a load of shit! Merely seeking out this outcome means exacting huge costs for fleeting benefits. I’m not talking about taking wild risks, but rather operating with common sense and reducing risks. Zero risk means zero progress and infinite cost. In many ways the desire for perfect safety and security is a power grab by those employed to do this sort of work. This desire is a disservice. They should be tasked with delivering good results with reasonable costs. Today we just write them a blank check. It is no wonder we can’t get work done and projects all come in late and over budget. This attitude exacts even greater costs on our long term safety and security.

As an example of the impact of this sort of lunacy consider an example. On any given day and for that day the safest thing to do is stay home and stay inside all day. You will shield yourself from driving, traffic, getting hit by a car, getting exposed to a virus and all sorts of other dangers. You will maximize your safety for that given day. If you run your life like this every single day, you will ruin your life. You will destroy your health, be lonely and fail to live. To live requires danger and risk. It requires putting yourself out there. Why do we think this safe at all costs attitude is right for society as a whole? It is not and the costs on all of us are piling up. We are not living like we should be.

Let’s get to the root of it

I’m not naive enough to believe this attitude comes out of the blue. A big reason is the loss of trust pervading society. We have had a huge regulatory response over the last 40-50 years that is the response to the lack of trust. Corporate behavior is a major reason for this. Under the mantra of maximizing shareholder value corporations will do all sorts of horrible things. Look at facebook for an example. They will commit all manners of harm to society to maximize clicks and ad revenue. Nothing except regulation stands in the way of doing harm to make money.

A proviso in the mantra of maximizing shareholder value is doing this within the confines of the law. The problem that has arisen over the past several decades is the capture of politics by money and by money from corporations. Increasingly we see corporations or those enriched by them as defining what the laws are. They are increasingly outside the reach of the law. The judiciary is aligned with this end. Most acutely through numerous Supreme Court decisions this process is accelerating. The most infamous of these decisions is Citizen’s United, which led to vast sums of corporate money distorting our politics. The only end of this process is an acceleration of loss of trust. Without a change this will end in violence or the end of democracy, or both. The same forces are dismantling regulation which was this bulwark and response to these forces to start with.

Puts the whole onus on prevention and none of the focus on improvement and progress. Progress is the main path to both security and safety. We are rapidly devolving into a society without enough trust to allow progress. Progress under the condition of trust is the way forward. Progress in science and culture has led to a better life for all. Medicine has eased suffering and extended lives. Science has given us a myriad of wonders like air travel and the internet. We have gained equality in culture for women and the LBGTQ community. Racial discrimination has faded from centrality culturally. More progress is needed, but crucially the progress made is at risk. All of this is threatened by the forces destroying the essential trust human society depends upon.

“What is progress? You might think that the question is so subjective and culturally relative as to be forever unanswerable. In fact, it’s one of the easier questions to answer. Most people agree that life is better than death. Health is better than sickness. Sustenance is better than hunger. Abundance is better than poverty. Peace is better than war. Safety is better than danger. Freedom is better than tyranny. Equal rights are better than bigotry and discrimination. Literacy is better than illiteracy. Knowledge is better than ignorance. Intelligence is better than dull-wittedness. Happiness is better than misery. Opportunities to enjoy family, friends, culture, and nature are better than drudgery and monotony. All these things can be measured. If they have increased over time, that is progress.”

― Steven Pinker

The costs are bigger than one can imagine

If I look closely at my life I can see the real cost of all this in the decay of the American research institutions. Over the past 40 years the great government laboratories have been destroyed by this dynamic. The lack of trust and inability to understand the benefits of research is crushing our science and technology edge. The Labs of the department of defense and NASA are shadows of their former glory. Remember that the internet came out of defense research. NASA started down the road to ruin after the moon landing then took final blows by the end of Reagan’s disasterous presidency. Now NASA is being brought further down by relying on Boeing for transport. Boeing is in the middle of riding maximizing shareholder value to the ruin of the company.

The DOE-NNSA Labs are a last bastion of American research. They are close to ruin. Over the course of my career, the Labs have been destroyed by the same attitudes. I distinctly remember the first ten years at Los Alamos being magical. The Lab was a wonderful crucible of knowledge, research and learning. Staff were generous with their time and expertise. I grew as a professional and flourished. Then it all ended. Like other institutions, fear and lack of trust entered. Actually it was already declining. Friends tell me that the Lab was even better in the years before I arrived. The generous spirit dried up and was replaced by suspicion and control. In the process research started to lose quality.

Breakthroughs no longer happened regularly with budget-money becoming the focus. No safety or security measure is too extreme. Cost be damned. Management became like business as private companies were the model of governance. The same attitudes revolving around maximizing shareholder value replace curiosity, inquiry and duty to the nation. Maximizing shareholder value has no meaning for the Labs, and yet it is the philosophy of governance. It has become toxic for companies (e.g., Boeing). It is idiotic for the Labs and a vehicle for catastrophe. Now the great

Labs of the USA are mere shadows of their former selves. We are all poorer for this. Recent studies have shown that the USA has completely lost its advantages in most science and technology. It has ceded its edge to China, India and Europe. We are to blame. The model of governance holds the murder weapon. Underneath this is the lack of trust infusing society. The pursuit of safety and security without regard for cost accelerates the process.

Let’s look at a couple of ways our fear and lack of trust play into this. Computer technology is the lifeblood of recent progress. We can see four distinct advances that shaped this period of time: Google search (its a verb now), the iPhone (smartphone), social media and large language models (i.e., ChatGPT). None of these came from the government labs. If you work at a government lab these advances are treated with fear and as risks. Their power is blunted by the fearful trust lacking management. Rather than harness the power of these breakthroughs, they are banned. They are castrated by rules. We see fear of technology and the inability to enable their power. Frankly we are a bunch of fucking morons and cowards. We have no leadership pushing back.

Let’s take this a step further. We see rules that seek to protect our work from prying eyes. Increasingly everything we do is classified in some way (lots of official use only that is now controlled unclassified information). This is just a way to hide things and not interact with the world. If we had a huge advantage this might make sense, but we don’t. We are not in the lead and these rules simply hold us back. They kill progress. Progress is what we need most of all now. The best thing all this hiding of information does is hide how incredibly incompetent we are. Increasingly we are hiding the embarrassingly backwards state of our technology. I am closing my career shaking my head on the collapse of our scientific supremacy.

“As people age, they confuse changes in themselves with changes in the world, and changes in the world with moral decline—the illusion of the good old days.” ― Steven Pinker