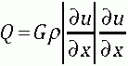The name of the original successful shock capturing method is “artificial viscosity,” and it is terrible. John Von Neumann and Robert Richtmyer were both mathematical geniuses, perhaps, at least in this case, poor at marketing. To be fair, they struggled with the name, and artificial viscosity was better than “mock” or “fictitious” viscosity, which Richtmyer considered in his earlier Los Alamos reports (LA-671 and LA-699). Nonetheless, we are left with this less than ideal name.
I’ve often wished I could replace this name with “shock viscosity” or better “shock dissipation” because the impact of artificial viscosity is utterly real. It is physical and necessary to compute the solutions of shocks automatically without resolving the ridiculously small length and time scales associated with the physical dissipation. In a very true sense, the magnitude of viscosity used in artificial viscosity is the correct amount of dissipation for the manner in which the shock is being represented.
The same issue comes about in the models of turbulence. Again, the effects of nonlinearity enormously augment the impact of physical dissipation. The nonlinearity is associated with complex small-scale structures whose details are unimportant to the large-scale evolution of the flow. When simulating these circumstances numerically we are often only interested in the large-scale flow field and we can use an enhanced (nonlinear) numerical viscosity to stably compute the flow. This approach in both shocks and turbulence has been ridiculously successful. In turbulence this approach goes by the name implicit large eddy simulation. It has been extremely controversial, but in the last decade this approach has grown in acceptance.
The key to this whole line of thinking is that dissipation is essential for physical behavior of numerical simulations. While too much dissipation is undesirable, too little dissipation is a disaster. The most dangerous situation is when a simulation is stable (that is, runs to completion), and produces seemingly plausible results, but has less dissipation than physically called for. In this case the simulation will produce an “entropy-violating” solution. In other words, the result will be unphysical, that is, not achievable in reality. This is truly dangerous and far less desirable than the physical, but overly dissipated result (IMHO). I’ve often applied a maxim to simulations, “when in doubt, diffuse it out”. In other words, dissipation while not ideal (a play on words!) is better than too little dissipation, which allows physically unachievable solutions to persist.
Too often numerical practitioners seek to remove numerical dissipation without being mindful of the delicate balance between, the dissipation that is excessive, and the necessity of dissipation for guaranteeing physically relevant (or admissible) results. It is a poorly appreciated aspect of nonlinear solutions for physical systems that the truly physical solutions are not those that have no dissipation, but rather produce a finite amount of dissipation. This finite amount is determined by the large-scale variations in the flow, and is proportional to the third power in these variations.
Very similar scaling laws exist for ideal incompressible and compressible flows. In the incompressible case, Kolmogorov discovered the scaling law in the 1940’s in the form of his refined similarity hypothesis, or the “4/5ths” law. Remarkably, Kolmogorov did this work in the middle of the Nazi invasion of the Soviet Union, and during the darkest days of the war for the Soviets. At nearly the same time in the United States, Hans Bethe discovered a similar scaling law for shock waves. Both can be written in stunningly similar forms where the time rate of change of kinetic energy due to dissipative processes (or change in entropy), is proportional to the third power of large-scale velocity differences, and completely independent of the precise value of viscosity.
These scaling laws are responsible for the success of artificial viscosity, and large eddy simulation. In fact, the origin of large eddy simulation is artificial viscosity. The original suggestion that led to the development of the first large eddy simulation by Smagorinsky was made by Von Neumann’s collaborator, Jules Charney to remove numerical oscillations from early weather simulations in 1956. Smagorinsky implemented this approach in three dimensions in what became the first large eddy simulation, and the first global circulation model. This work was the origin of a major theme in turbulence modeling, and climate modeling. The depth of this common origin has rarely been elaborated upon, but I believe the commonality has profound implications.
At the very least, it is important to realize that these different fields have a common origin. Dissipation isn’t something to be avoided at all costs, but rather something to manage carefully. Better yet, dissipation is something to be modeled carefully, and controlled. In numerical simulations, stability is the most important thing because without stability, the simulation is worthless. The second priority is producing a physically meaningful (or realizable) simulation. In other words, we want a simulation that produces a result that matches a situation achievable in the real world. The last condition is accuracy. We want a solution that is as accurate as possible, without sacrificing the previous two conditions.
Too often, the researcher gets hung up on these conditions in the wrong order (like prizing accuracy above all else). The practitioner applying simulations in an engineering context often does not prize accuracy enough. The goal is to apply these constraints in balance and in the right order (stability then realizability then accuracy). Getting the order and balance right is the key to high quality simulations.

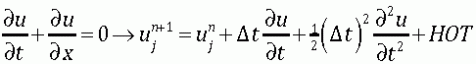
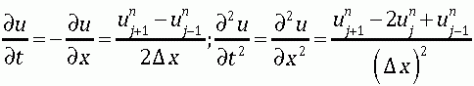
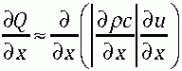
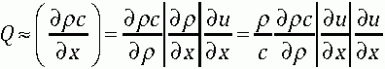
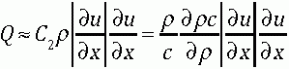
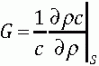 , (9)
, (9)