Judge a man by his questions rather than by his answers.

― Voltaire

In thinking about what makes work good for me, I explored an element of the creative process for me revolving around answering questions. If one doesn’t have the right question, the work isn’t framed correctly and progress will stall. A thing to consider in this frame of reference is what makes a good question? This itself is an excellent question! The quality of the question makes a great difference in framing the whole scientific enterprise, and can either lead to bad places of “knowledge cul-de-sacs” or open stunning vistas of understanding. Where you end up depends on the quality of the question you answer. Success depends far more on asking the right question than answering the question originally put to you (or you put to yourself).

truth, like gold, is to be obtained not by its growth, but by washing away from it all that is not gold.

― Leo Tolstoy

A great question is an achievement in itself although rarely viewed as such. More often than not little of the process of work goes into asking the right question. Often the questions we ask are highly dependent upon foundational assumptions that are never questioned. While assumptions about existing knowledge are essential, finding the weak or invalid assumptions is often the key to progress. These assumptions are wonderful for simplifying work, but also inhibit progress. Challenging assumptions is one of the most valuable things to do. Heretical ideas are fundamental to progress; all orthodoxy began as heresy. If the existing assumptions hold up under the fire of intense scrutiny they gain greater credibility and value. If they fall, new horizons are opened up to active exploration.

If we have no heretics we must invent them, for heresy is essential to health and growth.

― Yevgeny Zamyatin

It goes without saying that important questions are good ones. Defining importance is tricky business. There are plenty of important questions that lead nowhere “what’s the meaning of life?” or we simply can’t answer using existing knowledge, “is faster than light travel possible?” On the other hand we might do well to break these questions down to something more manageable that might be attacked, “is the second law of thermodynamics responsible for life?” or “what do subatomic particles tell us about the speed of light?” Part of the key to good scientific progress is threading the proverbial needle of important, worthy and possible to answer. When we manage to ask an important, but manageable question, we serve progress well. Easy questions are not valuable, but are attractive due to their lack of risk and susceptibility to management and planning. Sometimes the hardest part of the process is asking the question, and a well-defined and chosen problem can be amenable to trivial resolution. It turns out to be an immensely difficult task with lots of hard work to get to that point.

I have benefited mightily from asking some really great questions in the past. These questions have led to the best research, and most satisfying professional work I’ve done. I would love to recapture this spirit of work again, with good questioning work feeling almost quaint in today’s highly over-managed climate. One simple question occurred in my study of efficient methods for solving the equations of incompressible flow. I was using a pressure projection scheme, which involves solving a Poisson equation at least once, if not more than once a time step. The most efficient way to do this involved using the multigrid method because of its algorithmic scaling being linear. The Poisson equation involves solving a large sparse system of linear equations, and the solution of linear equations scales with powers of the number of equations. Multigrid methods have the best scaling thought to be possible (I’d love to see this assumption challenged and sublinear methods discovered, I think they might well be possible).

As problems with incompressible flows become more challenging such as involving large density jumps, the multigrid method begins to become fragile. Sometimes the optimal scaling breaks down, or the method fails altogether. I encountered these problems, but found that other methods like conjugate gradient could still solve the problems. The issue is that the conjugate gradient method is less efficient in its scaling than multigrid. As a result as problems become larger, the proportion of the solution time spent solving linear equations grows ever larger (the same thing is happening now to multigrid because of the cost of communication on modern computers). I posed the question of whether I could get the best of both methods, the efficiency with the robustness? Others were working on the same class of problems, and all of us found the solution. Combine the two methods together, effectively using a multigrid method to precondition the conjugate gradient method. It worked like a charm; it was both simple and stunningly effective. This approach has become so standard now that people don’t even think about it, its just the status quo.

At this point it is useful to back up and discuss a key aspect of the question-making process essential to refining a question into something productive. My original question was much different, “how can I fix multigrid?” was the starting point. I was working from the premise that multigrid was optimal and fast for easier problems, and conjugate gradient was robust, but slower. A key part of the process was a reframing the question. The question I ended up attacking was “can I get the positive attributes of both algorithms?” This changed the entire approach to solving the problem. At first, I tried switching between the two methods depending on the nature of the linear problem. This was difficult to achieve because the issues with the linear system are not apparent under inspection.

The key was moving from considering the algorithms as different options whole cloth, to combining them. The solution involved putting one algorithm inside the other. As it turns out the most reasonable and powerful way to do this is make multigrid a preconditioner for conjugate gradient. The success of the method is fully dependent on the characteristics of both algorithms. When multigrid is effective by itself, the conjugate gradient method is effectively innocuous. When multigrid breaks down, the conjugate gradient method picks up the pieces, and delivers robustness along with the linear scaling of multigrid. A key aspect of the whole development is embracing an assault on a philosophical constraint in solving linear systems. At the outset of this work these two methods were viewed as competitors. One worked on one or the other, and the two communities do not collaborate, or even talk to each other. They don’t like each other. They have different meetings, or different sessions at the same meeting. Changing the question allows progress, and is predicated on changing assumptions. Ultimately, the results win and the former feud fades into memory. In the process I helped create something wonderful and useful plus learned a huge amount of numerical (and analytical) linear algebra.

The second great question I’ll point to involved the study of modeling turbulent flows with what has become known as implicit large eddy simulation. Starting in the early 1990’s there was a stunning proposition that certain numerical methods seem to automatically (auto-magically) model aspects of turbulent flows. While working at Los Alamos and learning all about a broad class of nonlinearly stable methods, the claim that they could model turbulence caught my eye (I digested it, but fled in terror from turbulence!). Fast forward a few years and combine this observation with a new found interest in modeling turbulence, and a question begins to form. In learning about turbulence I digested a huge amount of theory regarding the physics, and our approaches to modeling it. I found large eddy simulation to be extremely interesting although aspects of the modeling were distressing. The models that worked well were performed poorly on the structural details of turbulence, and the models that matched the structure of turbulence were generally unstable. Numerical methods for solving large eddy simulation were generally based on principles vastly different than those I worked on, which were useful for solving Los Alamos’ problems.

Having methods I worked on for codes that do solve our problems also model turbulence is tremendously attractive. The problem is the seemingly magical nature of this modeling. Being magical does not endow the modeling with confidence. The question that we constructed a research program around was “can we explain the magical capability of numerical methods with nonlinear stability to model turbulence?” We combined the observation that a broad class of methods seemed to provide effective turbulence modeling (or the universal inertial range physics). Basically the aspects of turbulence associated with the large-scale hyperbolic parts of the physics were captured. We found that it is useful to think of this as physics-capturing as an extension of shock-capturing. The explanation is technical, but astoundingly simple.

Upon study of the origins of large eddy simulation we discovered that the origins of the method were the same as shock capturing methods. Once the method was developed it evolved into its own subfield with its own distinct philosophy, and underlying assumptions. These assumptions had become limiting and predicated on a certain point-of-view. Shock capturing had also evolved in a different direction. Each field focused on different foundational principles and philosophy becoming significantly differentiated. For the most part they spoke different scientific languages. It was important to realize that their origins were identical with the first shock capturing method being precisely the first subgrid model for large eddy simulation. A big part of our research was bridging the divides that had developed over almost five decades and learn to translate from one language to the other.

We performed basic numerical analysis of nonlinearly stable schemes using a technique that produced the nonlinear truncation error. A nonlinear analysis is vital here. This uses a technique known as modified equation analysis. The core property of the methods empirically known to be successful in capturing the physics of turbulence is conservation (control volume schemes). It turns out that the nonlinear truncation error for a control volume method for a quadratic nonlinearity produces the fundamental scaling seen in turbulent flows (and shocks for that matter). This truncation error can be destabilizing for certain flow configurations, effectively being anti-dissipative. The nonlinear stability method keeps the anti-dissipative terms under control, producing physically relevant solutions (e.g., entropy-solutions).

A key observation makes this process more reasoned and connected to the traditional large eddy simulation community. The control volume term matches the large eddy simulation models that produce good structural simulations of turbulence (the so-called scale similarity model). The scale similarity model is unstable with classical numerical methods. Nonlinear stability fixes this problem with aplomb. We use as much scale similarity as possible without producing unphysical or unstable results. This helps explain why a disparate set of principles used to produce nonlinear stability provides effective turbulence modeling. Our analysis also shows why some methods are ineffective for turbulence modeling. If the dissipative stabilizing effects are too large and competitive with the scale similarity term, the nonlinear stability is ineffective as a turbulence model.

It is dangerous to be right in matters on which the established authorities are wrong.

― Voltaire

I should spend some time on some bad questions as examples of what shouldn’t be pursued. One prime example is offered as a seemingly wonderful question, the existence of solutions to the incompressible Navier-Stokes equations. The impetus for this question is the bigger question of can we explain, predict or understand fluid turbulence? This problem is touted as a fundamental building block in this noble endeavor. The problem is the almost axiomatic belief that turbulence is contained within this model. The key term is incompressible, which renders the equations unphysical on several key accounts: it gives the system infinite speed of propagation, and divorces the equations from thermodynamics. Both features sever the ties of the equations from the physical universe. The arguing point is whether these two aspects disqualify it from addressing turbulence. I believe the answer is yes.

In my opinion this question should have been rejected long ago based on the available evidence. Given that our turbulence theory is predicated on the existence of singularities in ideal flows, and the clear absence of such singularities in the incompressible Navier-Stokes equations, we should reject the notion that turbulence is contained in them. Despite this evidence, the notion that turbulence is contained whole cloth in these unphysical equations remains unabated. It is treated as axiomatic. This is an example of an assumption that has out lived its usefulness. It will eventually be tossed out, and progress will bloom the path of its departure. One of the key things missing from turbulence is a connection to thermodynamics. Thermodynamics is such a powerful scientific concept and for it to be so absent from turbulence is a huge gap. Turbulence is a fundamental dissipative process and the second law is grounded on dissipation. The two should be joined into a coherent whole allowing unity and understanding to reign where confusion is supreme today.

Another poorly crafted question revolves around the current efforts for exascale class computers for scientific computing. There is little doubt that an exascale computer would be useful for scientific computing. A better question is what is the most beneficial way to push scientific computing forward? How can we make scientific computing more impactful in the real world? Can the revolution of mobile computing be brought to science? How can we make computing (really modeling and simulation) more effective in impacting scientific progress? Our current direction is an example of crafting an obvious question, with an obvious answer, but failing to ask a more cutting and discerning question. The consequence of our unquestioning approach to science will be wasted money and stunted progress.

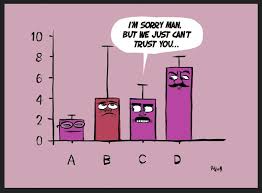
Trust is equal parts character and competence… You can look at any leadership failure, and it’s always a failure of one or the other.

― Stephen M.R. Covey

This gets at a core issue with how science is managed today. Science has never been managed more tightly and becoming more structurally mismanaged. The tight management of science as exemplified by the exascale computing efforts is driven by an overwhelming lack of trust in those doing science. Rather than ask people open-ended questions subject to refinement through learning, we ask scientists to work on narrowly defined programs with preconceived outcomes. The reality is that any breakthrough, or progress for that matter will take a form not envisioned at the outset of the work. Any work that pushes mankind forward will take a form not foreseeable. By managing so tightly and constraining work, we are predestining the outcomes to be stunted and generally unworthy of the effort put into them.

Whether you’re on a sports team, in an office or a member of a family, if you can’t trust one another there’s going to be trouble.

― Stephen M.R. Covey

This is seeded by an overwhelming lack of trust in people and science. Trust is a powerful concept and its departure from science has been disruptive and expensive. Today’s scientists are every bit as talented and capable as those of past generations, but society has withdrawn its faith in science. Science was once seen as a noble endeavor that embodied the best in humanity, but generally not so today. Progress in the state of human knowledge produced vast benefits for everyone and created the foundation for a better future. There was a sense of an endless frontier constantly pushing out and providing wonder and potential for everyone. This view was a bit naïve and overlooked the maxim that human endeavors in science are neither good or bad, producing outcomes dependent upon the manner of their use. For a variety of reasons, some embedded within the scientific community, the view of society changed and the empowering trust was withdrawn. It has been replaced with suspicion and stultifying oversight.

When I take a look at the emphasis in currently funded work, we see narrow vistas. There is a generally myopic and tactical view of everything. Long-term prospects, career development and broad objectives are obscured by management discipline and formality. Any sense of investment in the long-term is counter to the current climate. Nothing speaks more greatly to the overwhelming myopia is the attitude toward learning and personal development. It is only upon realizing that learning and research are essentially the same thing does it start to become clear how deeply we are hurting the scientific community. We have embraced a culture that is largely unquestioning with a well-scripted orthodoxy. Questions are seen as heresy against the established powers and punished. For most, learning is the acquisition of existing knowledge and skills. Research is learning new knowledge and skills. Generally speaking, those who have achieved mastery of their fields execute research. Since learning and deep career development is so hamstrung by our lack of trust, fewer people actually achieve the sort of mastery needed for research. The consequences for society are profound because we can expect progress to be thwarted.

Curiosity is more important than knowledge.

― Albert Einstein

One clear way to energize learning, and research is encouraging questioning. After encouraging a questioning attitude and approach to conducting work, we need to teach people to ask good questions, going back and refining questions, as better understanding is available. We need to identify and overcome assumptions subjecting them to unyielding scrutiny. The learning, research and development environment is equivalent to a questioning environment. By creating an unquestioning environment we short-circuit everything leading to progress, and ultimately cause much of the creative engine of humanity to stall. We would be well served by embracing the fundamental character of humanity as a creative, progressive and questioning species. These characteristics are parts of the best that people have to offer and allow each of us to contribute to the arc of history productively.

Curiosity is the engine of achievement.

― Ken Robinson

Brandt, Achi. “Multi-level adaptive solutions to boundary-value problems.” Mathematics of computation 31, no. 138 (1977): 333-390.

Briggs, William L., Van Emden Henson, and Steve F. McCormick. A multigrid tutorial. Society for Industrial and Applied Mathematics, 2000.

Kershaw, David S. “The incomplete Cholesky—conjugate gradient method for the iterative solution of systems of linear equations.” Journal of Computational Physics 26, no. 1 (1978): 43-65.

Melson, N. Duane, T. A. Manteuffel, and S. F. Mccormick. “The Sixth Copper Mountain Conference on Multigrid Methods, part 1.” (1993).

Puckett, Elbridge Gerry, Ann S. Almgren, John B. Bell, Daniel L. Marcus, and William J. Rider. “A high-order projection method for tracking fluid interfaces in variable density incompressible flows.” Journal of Computational Physics130, no. 2 (1997): 269-282.

Boris, J. P., F. F. Grinstein, E. S. Oran, and R. L. Kolbe. “New insights into large eddy simulation.” Fluid dynamics research 10, no. 4-6 (1992): 199-228.

Porter, David H., Paul R. Woodward, and Annick Pouquet. “Inertial range structures in decaying compressible turbulent flows.” Physics of Fluids 10, no. 1 (1998): 237-245.

Margolin, Len G., and William J. Rider. “A rationale for implicit turbulence modelling.” International Journal for Numerical Methods in Fluids 39, no. 9 (2002): 821-841.

Grinstein, Fernando F., Len G. Margolin, and William J. Rider, eds. Implicit large eddy simulation: computing turbulent fluid dynamics. Cambridge university press, 2007.

Fefferman, Charles L. “Existence and smoothness of the Navier-Stokes equation.” The millennium prize problems (2006): 57-67.

We don’t receive wisdom we must discover it for ourselves.

― Marcel Proust

Work is best when you start with a good question, analyze and learn until you discover and understand an answer to the question (questions often have many answers). Then you use this understanding to create something wonderful so that you can find a new and better question to answer. This virtuous cycle leads to be best work and provides the foundation for excellence. It is precisely the recipe for the best work experiences I’ve had, built my expertise and definitely how I’d prefer to keep doing work.

I’m on vacation this week (San Francisco is an amazing city!) and it is the perfect opportunity to think deeply about life and work. Work is an extremely important part of life, and I’ve concluded that some key things determine whether or not it is really good. The same things determine your ability to achieve excellence. What I’ve observed is a process that takes place leading up to my happiness and satisfaction. More importantly, it leads to great work, productivity and excellence. The elements of this successful recipe are founded on attacking a question that needs to be answered. This question can either come from something larger than myself, or simple innate personal curiosity. At the end of the process the question has been refined and answered yielding new understanding, knowledge, learning and tools to create something better. For me, the act of creation is the ultimate in job satisfaction for me. This is a virtuous cycle that leads to deep knowledge and the ability to recycle this process with an even better question using what has been learned and created.

Our real discoveries come from chaos, from going to the place that looks wrong and stupid and foolish.

― Chuck Palahniuk

The largest portion and most important part of this process is the analysis that allows us to answer the question. Often the question needs to be broken down into a series of simpler questions some of which are amenable to easier solution. This process is hierarchical and cyclical. Sometimes the process forces us to step back and requires us to ask an even better or more proper question. In sense this is the process working in full with the better and more proper question being an act of creation and understanding. The analysis requires deep work and often study, research and educating oneself. A new question will force one to take the knowledge one has and combine it with new techniques producing enhanced capabilities. This process is on the job education, and fuels personal growth and personal growth fuels excellence. When you are answering a completely new question, you are doing research and helping to push the frontiers of science forward. When you are answering an old question, you are learning and you might answer the question in a new way yielding new understanding. At worst, you are growing as a person and professional.

This is an utterly noble endeavor and embodies the best of mankind. At times you are simply pushing your self forward into areas others know very well already, but to you it is fresh and new. This is OK and even essential to get to the place where your work is unique. An under appreciated aspect of this sort of learning is the path you take is the potential to learn things in new ways. Your path is likely to be different than anyone else’s and grafts your own experience and understanding on to the topic anew. This is immensely valuable and can unveil new paths and depth to existing knowledge. Today this sort of thing is wholly unsupported and under appreciated. We need to make a new commitment to use this path to excellence.

The real voyage of discovery consists not in seeking new landscapes, but in having new eyes.

― Marcel Proust

Sometimes the question being answered has been well studied and one is simply discovering knowledge others have already mastered. This is important growth for a professional getting to the point where the frontier of knowledge exists. This is a necessary element in getting to research, which doesn’t happen automatically. One needs to climb up the mountain of human knowledge before getting to the apex. This is the process of education as a professional and an immensely exciting calling. The mastery of a topic requires many essential elements be mastered drawing together knowledge from diverse forces. Often the best research draws together rather pedestrian bits of knowledge from diverse fields in novel manners heretofore unseen before. When we don’t support this sort of endeavor, we smother important avenues of discovery and deny our society of the most important discoveries. Charting new paths to knowledge is either a wondrous personal journey and/or an alternative way to understand.

Discovery consists of looking at the same thing as everyone else and thinking something different.

― Albert Szent-Györgyi

Ultimately the elements are drawn together and allow the question to be answered productively. This often produces a new kernel of understanding. This knowledge can often be harnessed to produce the wherewithal for something new. The understanding will allow a new and unique act of creation. Sometimes you are creating something that others already know about, but for you it is new. That is enough for excellence; it is the engine of personal excellence. If you complete this cycle often enough eventually the creation will be genuinely original and new. The deep and powerful educational elements of this process leads to outstanding professionals well before one gets to genuinely new and unique research. It is essential to realize that very few creations are completely original with most discoveries being the combination of elements that are well known in other applications. In many cases the analysis and study of the answer to the original question itself creates something new and wonderful of many forms.

What is wanted is not the will to believe, but the will to find out, which is the exact opposite.

― Bertrand Russell

Once this creation is available, new questions can be posed and solved. These creations allow new questions to be asked answered. This is the way of progress where technology and knowledge builds the bridge something better. If we support excellence and a process like this, we will progress. Without support for this process, we simply stagnate and whither away. The choice is simple either embrace excellence by loosening control, or chain people to mediocrity.

Science is the process that takes us from confusion to understanding…

― Brian Greene

A very great deal more truth can become known than can be proven.

― Richard Feynman

In modeling and simulation verification is a set of activities broadly supporting the quality. Verification consists of two modes of practice: code verification where the mathematical correctness of the computer code is assessed, or solution (calculation) verification where the numerical error (uncertainty) is estimated. Both activities are closely linked to each other and they are utterly complementary in nature. To a large extent the methodology used for both types of verification are similar, but the differences between the two are important to maintain.

Modeling and simulation is an activity where continuous mathematics is converted to discrete computable quantities. This process involves approximation of the continuous mathematics and in almost every non-pathological circumstance is inexact. The core of modeling and simulation is the solution of (partial) differential equations using approximation methods. Code verification is a means of assuring that the approximations used to make the discrete solution of differential equations tractable on a computer are correct. A key aspect of code verification is determining that the discrete approximation of the differential equation is consistent with the continuous version of the differential equation.

Consistency demands that the order of approximation of the differential equation be at least one. In other words the discrete equations produce solutions that are the original continuous equations plus terms that are proportional to the size of the discretization. This character may be examined by solving problems with an exact analytical solution (or a problem with very well controlled and characterized errors) using several discretization sizes allowing the computation of errors, and determining the order of approximation. The combination of consistency and stability of the approximation means the approximation converges to the correct solution of the continuous differential equation.

We will examine both the nature of different types of problems to determine code verification and the methods of determining the order of approximation. One of the key aspects of code verification is the congruence of the theoretical order of accuracy for a method, and the observed order of accuracy. It is important to note that the theoretical order of convergence also depends upon the problem being solved. The problem must possess enough regularity to support the convergence rate expected. At this point it is important to point out that code verification produces both an order of approximation and an observed error in solution. Both of these quantities are important. For code verification, the order of approximation is the primary quantity of interest. It depends on both the nature of the approximation method and the problem being solved. If the problem being solved is insufficiently regular and smooth, the order of accuracy will not match the theoretical expectations of the method.

The second form of verification is solution verification. This is quite similar to code verification, but its aim is the estimation of approximation errors in a calculation. When one runs a problem without an analytical solution, the estimation of errors is more intricate. One looks at a series of solutions and compute the solution that is indicated by the sequence. Essentially the question of what solution is the approximation appearing to converge toward is being asked. If the sequence of solutions converges, the error in the solution can be inferred. As with code verification the order of convergence and the error is a product of the analysis. Conversely to the code verification, the error estimate is the primary quantity of interest, and the order of convergence is secondary.

 

 

The approach, procedure and methodology for both forms of verification are utterly complementary. Much of the mathematics and flow of work are shared in all verification, but details, pitfalls and key tips differ. In this post the broader themes of commonality are examined along with distinctions and a general rubric for each type of verification is discussed.

Code verification

Science replaces private prejudice with public, verifiable evidence.

― Richard Dawkins

When one conducts a code verification study there is a basic flow of activities and practices to conduct. One looks at a code to target and a problem to solve. Several key bits of information should be immediately being focused upon before the problem is solved. What is the order of accuracy for the method in the code being examined, and what is the order of accuracy that the problem being solved can expose? In addition the nature of the analytical solution to the problem should be carefully considered. For example what is the nature of the solution? Closed form? Series expansion? Numerical evaluation? Some of these forms of analytical solution have errors that must be controlled and assessed before the code’s method may be assessed. By the same token are there auxiliary aspects of the code’s solution that might pollute results? Solution of linear systems of equations? Stability issues? Computer roundoff or parallel computing issues? In each case these details could pollute results if not carefully excluded from consideration.

Next one needs to produce a solution on a sequence of meshes. For simple verification using a single discretization parameter only two discretizations are needed for verification (two equations to solve for two unknowns). For code verification the model for error is simple, generally a power law, where the error is proportional to the discretization parameter to the power (order) . There is also a constant of proportionality. The order, is the target of the study and one looks at its congruence with the expected theoretical order for the method on the problem being solved. It is almost always advisable to use more than the minimum number of meshes to assure that one simply isn’t examining anamolous behavior from the code.

One of the problems with code verification is the rarity of the observed order of convergence to exactly match the expected order of convergence. The question of how close is close enough haunts investigations. Invariably the observed order will deviate from the expected order by some amount. The question for the practitioner is how close is acceptable? Generally this question is given little attention. There are more advanced verification techniques that can put this issue to rest by producing uncertainties on the observed order, but the standard techniques simply produce a single result. Usually this results in rules of thumb that apply in broad brushes, but undermine the credibility of the whole enterprise. Often the criterion is that the observed order should be within a tenth of the theoretically expected result.

Another key caveat comes up when the problem is discontinuous. In this case the observed order is either set to one for nonlinear solutions, or weakly tied to the theoretical order of convergence. For the wave equation this result was studied by Banks, Aslam and Rider and admits an analytical and firmly determined result. In both cases the issue of inexact congruence with the expected rate of convergence remains. In addition for problems involving systems of equations will have multiple features each having a separate order of convergence, and the rates will combine within a solution. Ultimately in an asymptotic sense the lowest order of convergence will dominate as . This is quite difficult to achieve practically.

The last major issue that comes up in code verification (and solution verification too) is the nature of the discrete mesh and its connection to the asymptotic range of convergence. All of the theoretical results apply when the discretization parameter is small in a broad mathematical sense. This is quite problem specific and generally ill defined. Examining the congruence of the numerical derivatives of the analytical solution with the analytical derivatives can generally assess this. When these quantities are in close agreement, the solution can be considered to be asymptotic. Again these definitions are loose and generally applied with a large degree of professional or expert judgment.

It is useful to examine these issues through a concrete problem in code verification. The example I’ll use is a simple ordinary differential equation integrator for a linear equation coded up in Mathematica. We could solve this problem in a spreadsheet (like MS Excel), python, or a standard programming language. The example will look at two first order methods, forwards and backwards Euler methods. Both of these methods produce leading first order errors in an asymptotic sense, . If is large enough, the high order terms will pollute the error and produce deviations from the pure first-order error. Let’s look at this example and the concrete analysis from verification. This will be instructive in getting to similar problems encountered in general code verification.

Here is the code

ForwardEuler[h_, T_, a_] :=

(

uo = 1;

t = 0.0;

While[t < T,

(* integration *)

t = t + h;

un = uo + a h uo;

Print[“t= “, t, ” u(t) = “, un, ” err = “, Abs[un – Exp[a t]]];

uo = un

];

)

 

BackwardEuler[h_, T_, a_] :=

(

uo = 1;

t = 0.0;

While[t < T,

(* integration *)

t = t + h;

un = uo/(1 + a h);

Print[“t= “, t, ” u(t) = “, un, ” err = “, Abs[un – Exp[a t]]];

uo = un

];

)

Let’s look at the forward Euler integrator for several different choices of , different end times for the solution and number of discrete solutions using the method. We will do the same thing for the backwards Euler method, which is different because it is unconditionally stable with respect to step size. For this simple ODE, the method is stable to a stepsize of and we can solve the problem to two stopping times of , and . The analytical solution is always, . We can solve this problem using a set of step sizes, .

I can give results for various pairs of step sizes with both integrators, and see some common pathologies that we must deal with. Even solving such a simple problem, with simple methods can prove difficult and prone to heavy interpretation (arguably the simplest problem with the simplest methods). Much different results are achieved when the problem is run until different stopping times. We see the impactof accumulated error (since I’m using Mathematica so aspects of round-off error are pushed aside). In these cases round-off error would be another complication. Furthermore the backward Euler method for multiple equations would involve a linear (or nonlinear) solution that itself has an error tolerance that may significantly impact verification results. We see good results for and a systematic deviation for longer ending times. To get acceptable verification results would require much smaller step sizes (for longer calculations!). This shows how easy it is to scratch the surface of really complex behavior in verification that might mask correctly implemented methods. What isn’t so well appreciated is that this behavior is expected and amenable to analysis through standard methods extended to look for it.

h	FE T=1	FE T=10	FE T=100	BE T=1	BE T=10	BE T=100
1	1.64	0.03	~0	0.79	1.87	16.99
0.5	1.20	0.33	4e-07	0.88	1.54	11.78
0.25	1.08	0.65	0.002	0.93	1.30	7.17
0.125	1.04	0.83	0.05	0.96	1.16	4.07
0.0625	1.02	0.92	0.27	0.98	1.08	2.40
0.03125	1.01	0.96	0.55	0.99	1.04	1.63

Computed order of convergence for forward Euler (FE) and backward Euler (BE) methods for various stopping times and step sizes.

Types of Code Verification Problems and Associated Data

 Don’t give people what they want, give them what they need.

― Joss Whedon

The problem types are categorized by the difficulty of providing a solution coupled withthe quality of the solution that can be obtained.   These two concepts go hand-in-hand. As simple closed form solution is easy to obtain and evaluation. Conversely, a numerical solution of partial differential equations is difficult and carries a number of serious issues regarding its quality and trustworthiness. These issues are addressed by an increased level of scrutiny on evidence provided by associated data. Each of benchmark is not necessarily analytical in nature, and the solutions are each constructed in different means with different expected levels of quality and accompanying data. This necessitates the differences in level of required documentation and accompanying supporting material to assure the user of its quality.

Next, we provide a list of types of benchmarks along with an archetypical example of each. This is intended to be instructive to the experienced reader, who may recognize the example. The list is roughly ordered in increasing level of difficulty and need for greater supporting material.

• Closed form analytical solution (usually algebraic in nature). Example: Incompressible, unsteady, 2-D, laminar flow over an oscillating plate (Stokes oscillating plate) given in Panton, R. L. (1984). Incompressible Flow, New York, John Wiley, pp. 266-272.
• Analytical solution with significantly complex numerical evaluation
  • Series solution. Example: Numerous classical problems, in H. Lamb’s book, “Hydrodynamics,” Dover, 1932. Classical separation of variables solution to heat conduction. Example: Incompressible, unsteady, axisymmetric 2-D, laminar flow in a circular tube impulsively started (Szymanski flow), given in White, F. M. (1991). Viscous Fluid Flow, New York, McGraw Hill, pp. 133-134.
  • Nonlinear algebraic solution. Example: The Riemann shock tube problem, J. Gottleib, C. Groth, “Assessment of Riemann solvers for unsteady one-dimensional inviscid flows of perfect gases,” Journal of Computational Physics, 78(2), pp. 437-458, 1988.
  • A similarity solution requiring a numerical solution of nonlinear ordinary differential equations.
  • Manufactured Solution. Example: Incompressible, steady, 2-D, turbulent, wall-bounded flow with two turbulence models (makes no difference to me), given in Eça, L., M. Hoekstra, A. Hay and D. Pelletier (2007). “On the construction of manufactured solutions for one and two-equation eddy-viscosity models.” International Journal for Numerical Methods in Fluids. 54(2), 119-154.
• Highly accurate numerical solution (not analytical). Example: Incompressible, steady, 2-D, laminar stagnation flow on a flat plate (Hiemenz flow), given in White, F. M. (1991). Viscous Fluid Flow, New York, McGraw Hill. pp. 152-157.
• Numerical benchmark with an accurate numerical solution. Example: Incompressible, steady, 2-D, laminar flow in a driven cavity (with the singularities removed), given in Prabhakar, V. and J. N. Reddy (2006). “Spectral/hp Penalty Least-Squares Finite Element Formulation for the Steady Incompressible Navier-Stokes Equations.” Journal of Computational Physics. 215(1), 274-297.
• Code-to-code comparison data. Example: Incompressible, steady, 2-D, laminar flow over a back-step, given in Gartling, D. K. (1990). “A Test Problem for Outflow Boundary Conditions-Flow Over a Backward-Facing Step.” International Journal for Numerical Methods in Fluids. 11, 953-967.

Below is a list of the different types of data associated with verification problems defined above. Depending on the nature of the test problem only a subset of these data are necessary. This will be provided below the list of data types. As noted above, benchmarks with well-defined closed form analytical solutions require relatively less data than a benchmark associated with the approximate numerical solution of PDEs.

• Detailed technical description of the problem (report or paper)
• Analysis of the mathematics of the problem (report or paper)
• Computer analysis of solution (input file)
• Computer solution of the mathematical solution
• Computer implementation of the numerical solution
• Error analysis of the “exact” numerical solution
• Derivation of the source term and software implementation or input
• Computer implementation of the source term (manufactured solution)
• Grids for numerical solution
• Convergence and error estimation of approximate numerical solution
• Uncertainty and sensitivity study of numerical solution
• Description and analysis of computational methods
• Numerical analysis theory associated with convergence
• Code description/manuals
• Input files for problems and auxiliary software
• Patch test description, Derivation, input and analysis
• Unusual boundary conditions (inflow, piston, etc.…)
• Physics restrictions (boundary layer theory, inviscid,)
• Software quality documents
• Scripts and auxiliary software for verification
• Source code
• Metric descriptions
• Verification results including code version, date, etc.
• Numerical sensitivity studies
• Feature coverage in verification

Below, we briefly describe the characteristics of each type of benchmark documentation (could be called artifacts or meta-data) associated with a code verification benchmarks. These artifacts take a number of concrete forms such as a written document, computer code, mathematical solution in document or software form, input files for executable codes, input to automatic computer analysis, output from software quality systems, among others.

• Detailed technical description of the benchmark (report or paper): This can include a technical paper in a journal or conference proceeding describing the benchmark and its solution. Another form would be a report informal or formal from an institution providing the same information.
• Analysis of the mathematics (report or paper): For any solution that is closed form, or requiring a semi-analytical solution, the mathematics must be described in detail. This can be included in the paper (report) discussed previously or in a separate document.
• Computer analysis of solution (input file): If the mathematics or solution is accomplished using a computerized analysis, the program used and the input to the program should be included. Some sort of written documentation such as a manual for the software ideally accompanies this artifact.
• Computer solution of the mathematical solution: The actual computerized solution of the mathematical problem should be included in whatever form the computerized solution takes. This should include any error analysis completed with this solution.
• Computer implementation of the numerical solution: The analytical solution should be implemented in a computational form to allow the comparison with the numerical solution. This should include some sort of error analysis in the form of a report.
• Derivation of the source term and software implementation or input: In the case of the method of manufactured solutions, the source term used to drive the numerical method must be derived through a well-defined numerical procedure. This should be documented through a document, and numerical tools used for the derivation and implementation.
• Computer implementation of the source term (manufactured solution): The source term should be included in a form amenable to direct use in a computer code. The language for the computer code should be clearly defined as well as the compiler and computer system used.
• Grids for numerical solution: If a solution is computed using another simulation code all relevant details on the numerical grid(s) used must be included. This could be direct grid files, or input files to well-defined grid generation software.
• Convergence and error estimation of numerical solution: The numerical solution must include a convergence study and error estimate. These should be detailed in an appropriately peer-reviewed document.
• Uncertainty and sensitivity study of numerical solution: The various modeling options in the code used to provide the numerical solution must be examined vis-a-vis the uncertainty and sensitivity of the solution to these choices. This study should be used to justify the methodology used for the baseline solution.
• Description and analysis of computational methods: The methods used by the code used for the baseline solution must be completely described and analyzed. This can take the form of a complete bibliography of readily available literature
• Numerical analysis theory associated with convergence: The nature of the convergence and the magnitude of error in the numerical solution must be described and demonstrated. This can take the form of a complete bibliography of readily available literature.
• Code description/manuals: The code manual and complete description must be included with the analysis and description.
• Input files for benchmarks and auxiliary software: The input file used to produce the solution must be included. Any auxiliary software used to produce or analyze the solution must be full described or included.
• Unusual boundary conditions (inflow, piston, outflow, Robin, symmetry, …): Should the benchmark require unusual or involved boundary or initial conditions, these must be described in additional detail including the nature of implementation.
• Physics restrictions (boundary layer theory, inviscid, parabolized Navier-Stokes, …): If the solution requires the solution of a reduced or restricted set of equations, this must be fully described. Examples are boundary layer theory, truly inviscid flow, or various asymptotic limits.
• Software quality documents: Of non-commercial software used to produce solutions, the software quality pedigree should be clearly established by documenting the software quality and steps taken to assure the maintenance of the quality.
• Scripts and auxiliary software for verification: Auxiliary software or scripts used to determine the verification or compute error estimates for a software used to produce solution should be included.
• Source code: If possible the actual source code for the software along with instructions for producing an executable (makefile, scripts) should be included with all other documentation.
• A full mathematical or computational description of metrics used in error analysis and evaluation of solution implementation or numerical solution.
• Verification results including code version, date, and other identifying characteristics: The verification basis for the code used to produce the baseline solution must be included. This includes any documentation of verification, peer-review, code version, date completed and error estimates.
• Feature coverage in verification: The code features covered by verification benchmarks must be documented. Any gaps where the feature used for the baseline solution are not verified must be explicitly documented.

Below are the necessary data requirements for each category of benchmark, again arranged in order of increasing level of documentation required. For completeness each data type would expected to be available to describe a benchmark of a given type.

• Common elements for all types of benchmarks (it is notable that the use of proper verification using an analytical solution results in the most compact set of requirements for data, manufactured solutions also).

1. Paper or report
2. Mathematical analysis
3. Computerized solution and input
4. Error and uncertainty analysis
5. Computer implementation of the evaluation of the solution
6. Restrictions
7. Boundary or initial conditions

• Closed form analytical solution

1. Paper or report
2. Mathematical analysis
3. Computerized solution and input
4. Error and uncertainty analysis
5. Computer implementation of the evaluation of the solution
6. Restrictions
7. Boundary or initial conditions

• Manufactured Solution

1. Paper or report
2. Mathematical analysis
3. Computational solution and input
4. Error and uncertainty analysis
5. Computer implementation of the evaluation of the solution
6. Derivation and implementation of the source term
7. Restrictions
8. Boundary or initial conditions

• Numerical solution with analytical solution
• Series solution, Nonlinear algebraic solution, Nonlinear ODE solution

1. Paper or report
2. Mathematical analysis
3. Computerized solution and input
4. Error and uncertainty analysis
5. Computer implementation of the evaluation of the solution
6. Input files
7. Source code
8. Source code SQA
9. Method description and manual
10. Restrictions
11. Boundary or initial conditions

• Highly accurate numerical solution (not analytical), numerical benchmarks or code-to-code comparisons.

1. Paper or report
2. Mathematical analysis
3. Computational solution and input
4. Error and uncertainty analysis for the solution
5. Computer implementation of the evaluation of the solution
6. Input files
7. Grids
8. Source code
9. Source code SQA
10. Method description and manual
11. Method analysis
12. Method verification analysis and coverage
13. Restrictions
14. Boundary or initial conditions

The use of direct numerical simulation requires a similar or even higher level of documentation than analytical solutions. This coincides with the discussion of the last type of verification benchmark where a complex numerical method with significant approximations is utilized to produce the solution. As a numerically computed benchmark, the burden of proof is much larger.   Code verification is best served by exact analytical solutions because of the relative ease in assuring benchmark solution accuracy. Nonetheless, it remains a common practice due to its inherent simplicity. It also appeals to those who have a vested interest in the solutions produced by a certain computer code. The credibility of the comparison is predicated on the credibility of the code producing the “benchmark” used as the surrogate for truth. Therefore the documentation of the benchmark must provide the basis for the credibility.

The use of DNS as a surrogate for experimental data has received significant attention. This practice violates the fundamental definition of validation we have adopted because no observation of the physical world is used to define the data. This practice also raises other difficulties, which we will elaborate upon. First the DNS code itself requires that the verification basis further augmented by a validation basis for its application.   This includes all the activities that would define a validation study including experimental uncertainty analysis numerical and physical equation based error analysis. Most commonly, the DNS serves to provide validation, but the DNS contains approximation errors that must be estimated as part of the “error bars” for the data. Furthermore, the code must have documented credibility beyond the details of the calculation used as data. This level of documentation again takes the form of the last form of verification benchmark introduced above because of the nature of DNS codes. For this reason we include DNS as a member of this family of benchmarks.

There are two ways to do great mathematics. The first is to be smarter than everybody else. The second way is to be stupider than everybody else — but persistent.

― Raoul Bott

Banks, Jeffrey W., T. Aslam, and William J. Rider. “On sub-linear convergence for linearly degenerate waves in capturing schemes.” Journal of Computational Physics 227, no. 14 (2008): 6985-7002.

Greenough, J. A., and W. J. Rider. “A quantitative comparison of numerical methods for the compressible Euler equations: fifth-order WENO and piecewise-linear Godunov.” Journal of Computational Physics 196, no. 1 (2004): 259-281.

Kamm, James R., Jerry S. Brock, Scott T. Brandon, David L. Cotrell, Bryan Johnson, Patrick Knupp, W. Rider, T. Trucano, and V. Gregory Weirs. Enhanced verification test suite for physics simulation codes. No. LLNL-TR-411291. Lawrence Livermore National Laboratory (LLNL), Livermore, CA, 2008.

Rider, J., James R. Kamm, and V. Gregory Weirs. “Verification, Validation and Uncertainty Quantification Workflow in CASL.” Albuquerque, NM: Sandia National Laboratories (2010).

Rider, William J., James R. Kamm, and V. Gregory Weirs. “Procedures for Calculation Verification.” Simulation Credibility (2016): 31.

He who has a why to live for can bear almost any how.
― Friedrich Nietzsche

At work we often justify the research we do through declaring that it is mission-relevant, or mission-focused. The work is automatically important and necessary if it supports our mission. Defining the mission is then essential to this conversation. Currently in my work, the discussion of what the mission is focuses on high performance computing. The pregnant question is whether my work’s mission is high performance computing?

I unilaterally reject this as a mission.

High performance computing is a “how” and so is “modeling and simulation” for that matter. Both things are tools to conduct science and engineering specialized to a purpose. Neither is a viable mission or reason in and of itself. Missions are better defined as “what’s” like nuclear weapons, economic competitiveness or scientific investigation. The high performance computing is how modeling and simulation is done, which is how aspects of nuclear weapons work or science or industrial work is done, but certainly not all of any of these. We still haven’t gotten to why we do these things. Why we fund high performance computing for modeling and simulation to support the nuclear weapons stockpile is an intricate question worth some further exploration.

A knee jerk response is “National Security,” which avoids a deeper discussion. The defense of a Nation State is associated with ability of the citizens of that Nation to achieve a degree of access to resources that raise their access to a good life. With more resources the citizens can aspire toward a better, easier more fulfilled life. In essence the security of a Nation can allow people to exist higher on Maslow’s hierarchy needs. In the United States this is commonly expressed as “freedom”. Freedom is a rather superficial thing when used as a slogan. The needs of the citizens begin with having food and shelter than allow them to aspire toward a sense of personal safety. Societal safety is one means of achieving this (not that safety and security are pretty low on the hierarchy). With these in hand, the sense of community can be pursued and then sense of an esteemed self. Finally we get to the peak and the ability to pursue ones full personal potential.

At the lowest part of the hierarchy is subsistence, the need for basic resources to survive. If one exists at this level, life isn’t very good, but its achievement is necessary for a better life. Gradually one moves up the hierarchy requiring greater access to resources and ease of maintaining the lower positions on the hierarchy. A vibrant National Security should allow this to happen, the richer a Nation becomes the higher on the hierarchy of needs its citizens reside. It is with some recognition of irony that my efforts and the Nation is stuck at such a low level on the hierarchy. Efforts toward bolstering the community the Nation forms seem to be too difficult to achieve today. We seem to be regressing from being a community or achieving personal fulfillment. We are stuck trying to be safe and secure. The question is whether those in the Nation can effectively provide the basis for existing high on the hierarchy of needs without being there themselves?

My observation about my work is that the people doing the work to support National Security are moving to lower and lower levels of the hierarchy by being isolated from the “why’s” of their work, and pushed into a subsistence existence focused on the “how’s”. Increasingly the work is even divorced from the “what’s” and the “why” is never even considered. As a result people simply do what they are told without considering what it is for, or why they are doing it. The result is a decline in the quality and applicability of the foundational work, which should adapt to the needs of its use and inspired by the underlying reasons. This issue is rampant in high performance computing where its utility for modeling and simulation is intellectually threadbare, and those working in computing barely consider what any of their work will be used for.

We are seeing our scientific community pushed to ever lower rungs Maslow’s pyramid. Part of this is the pervasive distrust of experts and education in the United States and perhaps the entirety of the West. These problems are harbingers of decline and hardly support the expansion and vibrancy of democracy or freedom.

 

 

 

Rigor alone is paralytic death, but imagination alone is insanity.

― Gregory Bateson

Solving hyperbolic conservation laws provides a rich vein of knowledge to mine and utilize more generally. Most canonically this involves solving the equations of gas dynamics, but the lessons apply to a host of other equations such as magneto-hydrodynamics, multi-material hydrodynamics, oil-water flow, solid mechanics, and on and on. Gas dynamics is commonly visible in the real world, and includes lots of nonlinearity, structure and complexity to contend with. The structures and complexity includes compressible flow structures such as shock waves, rarefactions and contract discontinuities. In more than one dimension you have shear waves, and instabilities that ultimately lead to turbulent flows. With all of these complications to deal with, these flows present numerous challenges to their robust, reliable and accurate simulation. As such, gas dynamics provides a great springboard for robust methods in many fields as well as a proving ground for much of applied math, engineering and physics. It provides a wonderful canvas for the science and art of modeling and simulation to be improved in the vain, but beneficial attempt at perfection.

Getting a basic working code can come through a variety of ways using some basic methods that provide lots of fundamental functionality. Some of the common options are TVD methods (ala Sweby for example), high order Godunov methods (ala Colella et al), FCT methods (ala Zalesak), or even WENO (Shu and company). For some of these methods the tricks leading to robustness make it into print (Colella, Zalesak come to mind in this regard). All of these will give a passable to even a great solution to most problems, but still all of them can be pushed over the edge with a problem that’s hard enough. So what defines a robust calculation? Let’s say you’ve taken my advice and brutalized your code https://williamjrider.wordpress.com/2017/06/09/brutal-problems-make-for-swift-progress/ and now you need to fix your method https://williamjrider.wordpress.com/2017/06/16/that-brutal-problem-broke-my-code-what-do-i-do/. This post will provide you with a bunch of ideas about techniques, or recipes to get you across that finish line.

You can’t really know what you are made of until you are tested.

― O.R. Melling

The starting basis for getting a robust code is choosing a good starting point, a strong foundation to work from. Each of the methods above would to a significant degree define this. Opinions differ on which of the available options are best, so I won’t be prescriptive about it (I prefer high-order Godunov methods in the interest of transparency). For typical academic problems, this foundation can be drawn from a wide range of available methods, but these methods often are not up to the job in “real” codes. There are a lot more things to add to a method to get you all the way to a production code. These are more than just bells and whistles; the techniques discussed here can be the difference between success and failure. Usually these tricks of the trade are found through hard fought battles and failures. Each failure offers the opportunity to produce something better and avoid problems. The best recipes produce reliable results for the host of problems you ask the code to solve. A great method won’t fall apart when you ask it to do something new either.

The methods discussed above all share some common things. First and foremost is reliance upon a close to bulletproof first order method as the ground state for the higher order method. This is the first step in building robust methods, start with a first-order method that is very reliable and almost guaranteed to give a physically admissible solution. This is easier said than done for general cases. We know that theoretically the lowest dissipation method with all the necessary characteristics is Godunov’s method (see Osher’s work from the mid-1980’s). At the other end of the useful first-order method spectrum is Lax-Friedrichs method, the most dissipative stable method. In a sense these methods give us our bookends. Any method we use as a foundation will be somewhere between these two. Still coming up with a good foundational first-order method is itself an art. The key is choosing a Riemann solver that provides a reliable solution under even pathological circumstances (in lieu of a Riemann solver, a dissipation that is super reliable).

You cannot build a dream on a foundation of sand. To weather the test of storms, it must be cemented in the heart with uncompromising conviction.

― T.F. Hodge

Without further ado let’s get to the techniques that one ought to use. The broadest category of techniques involves adding smart dissipation to methods. This acknowledges that the methods we are using already have a lot of dissipative mechanisms built into them. As a result the added dissipation needs to be selective as hell. The starting point is a careful statement of where the methods already have dissipation. Usually it lies in two distinct places, the most obvious being Riemann solvers or artificial viscosity. The Riemann solver adds an upwind bias to the approximation, which has an implicit dissipative content. The second major source of dissipation is the discretization itself, which can include biases that provide implicit dissipation. For sufficiently complex or nonlinear problems the structural dissipation in the methods are not enough for nonlinear stability. One of the simplest forms for this dissipation is the addition of another dissipative form. For Godunov methods the Lapidus viscosity can be useful because it works at shocks, and adds a multidimensional character. Other viscosity can be added through the Riemann solvers (via so-called entropy fixes, or selecting larger wavespeeds since dissipation is proportional to that). It is important that the dissipation be mechanistically different than the base viscosity, meaning that hyperviscosity (https://williamjrider.wordpress.com/2016/03/24/hyperviscosity-is-a-useful-and-important-computational-tool/) can really be useful to augment dissipation. A general principle is to provide multiple alternative routes to nonlinear stability to support each other effectively.

The building blocks that form the foundation of your great and successful future, are the actions you take today

― Topsy Gift

The second source of dissipation is the fundamental discretization, which implicitly provides it. One of the key aspects of modern discretization are limiters that provide nonlinear stability through effectively adapting the discretization to the solution. These limiters come in various forms, but they all provide the means for the method to choose a favorable discretization for the nature of the solution (https://williamjrider.wordpress.com/2016/06/22/a-path-to-better-limiters/, https://williamjrider.wordpress.com/2016/06/14/an-essential-foundation-for-progress/, https://williamjrider.wordpress.com/2016/06/03/nonlinear-methods-a-key-to-modern-modeling-and-simulation/ ). One of the ways for additional dissipation to enter the method is through a deliberate choice of different limiters. One can bias the adaptive selection of discretization toward more dissipative methods when the solution calls for more care. These choices are important to make when solutions have shock waves, complex nonlinear structures, oscillations, or structural anomalies. For example the minmod limiter based method is the most dissipative second-order, monotonicity-preserving method. It can be used as a less dissipative alternative safety net instead of the first-order methods although its safety is predicated on a bulletproof first order method as a foundation.

Except for all but the most ideal circumstances, the added dissipation is not sufficient to produce a robust method. Very strong nonlinear events that confound classical analysis can still produce problems. All oscillations are very difficult to remove from the solutions and can work to produce distinct threats to the complete stability of the solution. Common ways to deal with these issues in a rather extreme manner are floors and ceilings for various variables. One of the worst things that can happen is a physical quantity moving outside its physically admissible bounds. The simplest example is a density going negative. Density is a positive definite quantity and needs to stay that way for the solution to be physical. It behooves robustness to make sure this does not happen. If it does it is usually catastrophic for the code. This is a simple case and in general quantities should lie within reasonable bounds. Usually when quantities fall outside reasonable bounds the code’s solutions are compromised. It makes sense to explicitly guard against this specifically where a quantity being out of bounds would general a catastrophic effect. For example, sound speeds involve densities and pressure plus a square root operation; a negative value would be disaster.

One can take things a long way toward robustness through using methods that more formally produce bounded approximations. The general case of positivity, or more bounded approximation has been pursued actively. I described the implementation of methods of this sort earlier, (https://williamjrider.wordpress.com/2015/08/06/a-simple-general-purpose-limiter/ ). These methods can go a very long way to giving the robust character one desires, but other means discussed above are still necessary. A large production code with massive meshes and long run times will access huge swaths of phase space and as the physical complexity of problems increases, almost anything that can happen will. It is foolish to assume that bad states will not occur. One also must contend with people using the code in ways the developers never envisioned, and putting the solver into situations where it must survive even when it was designed for them. As a consequence it would be foolish to completely remove the sorts of checks that avert disaster (this could be done, but only with rigorous testing far beyond what most people ever do).

What to concretely do is another question where there are multiple options. One can institute a floating-point trap that locally avoids the possibility of using a negative value for the square root. This can be done in a variety of ways with differing benefits and pitfalls. One simple approach is to take the square root of the absolute value, or one might choose the max of the density and some sort of small floor value. This does little to address the core reason that the approximations produced an unphysical value. There is also little control on the magnitude of the density (the value can be very small), which has rather unpleasant side effects. A better approach would get closer to the root of the problems, which almost without fail comes from the inappropriate application of high-order approximations. One way for this to be applied is to replace the high-order approximations with a physically admissible low-order approximation. This relies upon the guarantees associated with the low-order (first order) approximation as a general safety net for the computational method. The reality is that the first-order method can also go bad, and the floating-point trap may or certainly be necessary even there.

A basic part of the deterministic solution to many problems is the ability to maintain symmetry. The physical world almost invariably breaks symmetry, but it is arguable that numerical solutions to the PDEs should not (I could provide the alternative argument vigorously too). If you want to maintain such symmetry, the code must be carefully designed to do this. A big source of the symmetry breaking is upwind approximations, especially if one choses a bias where zero isn’t carefully and symmetrically treated. One approach is the use of smoothed operators that I discussed at length (https://williamjrider.wordpress.com/2017/03/24/smoothed-operators/, https://williamjrider.wordpress.com/2017/03/29/how-useful-are-smoothed-operators/, https://williamjrider.wordpress.com/2017/04/04/results-using-smoothed-operators-in-actual-code/ ). More generally the use of “if” tests in the code will break symmetry. Another key area for symmetry breaking is the solution of linear systems by methods that are not symmetry preserving. This means numerical linear algebra needs to be carefully approached.

For gas dynamics, the mathematics of the model provide us with some very general character to the problems we solve. Shock waves are the preeminent feature of compressible gas dynamics, and a relatively predominant focal point for methods’ development and developer attention. Shock waves are nonlinear and naturally steepen thus countering dissipative effects. Shocks benefit through their character as garbage collectors, they are dissipative features and as a result destroy information. Some of this destruction limits the damage done by poor choices of numerical treatment. Being nonlinear one has to be careful with shocks. The very worst thing you can do is to add too little dissipation because this will allow the solution to generate unphysical noise or oscillations that are emitted by the shock. These oscillations will then become features of the solution. A lot of the robustness we seek comes from not producing oscillations, which can be best achieved with generous dissipation at shocks. Shocks receive so much attention because their improper treatment is utterly catastrophic, but they are not the only issue; the others are just more subtle and less apparently deadly.

Rarefactions are the benign compatriot to shocks. Rarefactions do not steepen and usually offer modest challenges to computations. Rarefactions produce no dissipation and their spreading nature reduces the magnitude of anything anomalous produced by the simulation. Despite their ease relative to shock waves, the rarefactions do produce some distinct challenges. The simplest case involves centered rarefactions where the characteristic velocity of the rarefaction goes to zero. Since dissipation in methods is proportional to the characteristic velocity, the presence of zero dissipation can trigger disaster and can generate completely unphysical rarefaction shocks (rarefaction shocks can be physical for exotic BZT fluids). More generally for very strong rarefactions one can see small and very worrisome deviations from adhering to the second law, these should be viewed with significant suspicion. The other worrisome feature of most computed rarefactions is the structure of the head of the rarefaction. Usually there is a systematic bump there that is not physical and may produce unphysical solutions for problems featuring very strong expansion waves. This bump actually looks like a shock when viewed through the lens of Lax’s version of the entropy conditions (based on characteristic velocities). This is an unsolved problem at present and represents a challenge to our gas dynamics simulations. The basic issue is that a strong enough rarefaction cannot be solved in an accurate, convergent manner by existing methods.

A third outstanding feature of gas dynamics are contact discontinuities, which are classified as linearly degenerate waves. They are quite similar to linear waves meaning that the characteristics do not change across the wave; for the ideal analysis the jumps neither steepen nor spread across the wave. One of the key results is that any numerical error is permanently encoded into the solution. One needs to be careful with dissipation because it never goes away. For this reason people consider steepening the wave to keep it from artificially spreading. It is a bit of an attempt to endow the contact with a little of the character of a shock courting potential catastrophe in the process. This can be dangerous if it is applied to with an interaction with a nonlinear wave, or instability for multidimensional flows. Another feature of the contact is their connection to multi-material interfaces as a material interface can ideally be viewed as a contact. Multi-material flows are a deep well of significant problems and a topic of great depth unto themselves (Abgrall and Karni is an introduction which barely scratches the surface!).

The fourth standard feature is shear waves, which are a different form of linearly degenerate waves. Shear waves are heavily related to turbulence, thus being a huge source of terror. In one dimension shear is rather innocuous being just another contact, but in two or three dimensions our current knowledge and technical capabilities are quickly overwhelmed. Once you have a turbulent flow, one must deal with the conflation of numerical error, and modeling becomes a pernicious aspect of a calculation. In multiple dimensions the shear is almost invariably unstable and solutions become chaotic and boundless in terms of complexity. This boundless complexity means that solutions are significantly mesh dependent, and demonstrably non-convergent in a point wise sense. There may be a convergence in a measure-valued sense, but these concepts are far from well defined, fully explored and technically agreed upon.

A couple of general tips for developing a code involves the choice of solution variables. All most without fail, the worst thing you can do is define the approximations using the conserved quantities. This is almost always a more fragile and error prone manner to compute solutions. In general the best approach is to use the so-called primitive variables (https://williamjrider.wordpress.com/2016/08/08/the-benefits-of-using-primitive-variables/ ). The variables are clear in their physical implications and can be well-bounded using rational means. Using primitive variables is better for almost anything you want to do. The second piece of advice is to use characteristic variables to as great an extent as possible. This always implies some sort of one-dimensional thought. Despite this limitation, the benefits of characteristic variables are so extreme as to justify their use even under these limited circumstances.

A really good general rule is to produce thermodyanically consistent solutions. In other words, don’t mess with thermodynamic consistency, and particularly with the second law of thermodynamics. Parts of this thermodynamic consistency are the dissipative nature of physical solutions and the active adherence to entropy conditions. There are several nuances to this adherence that are worth discussing in more depth. It is generally and commonly known that shocks increase entropy. What isn’t so widely appreciated is the nature of this increase being finite and adheres to a scaling that is proportional to the size of the jump. The dissipation does not converge toward zero, but rather toward a finite value related to the structure of the solution.

The second issue is dissipation free nature of the rest of the flow especially rarefactions. The usual aim of solvers is to completely remove dissipation, but that runs the risk of violating the second law. It may be more advisable to keep a small positive dissipation working (perhaps using a hyperviscosity partially because control volumes add a nonlinear anti-dissipative error). This way the code stays away from circumstances that violate this essential physical law. We can work with other forms of entropy satisfaction too. Most notably is Lax’s condition that identifies the structures in a flow by the local behavior of the relevant characteristics of the flow. Across a shock the characteristics flow into the shock, and this condition should be met with dissipation. These structures are commonly present in the head of rarefactions.

One of the big things that can be done to improve solutions is the systematic use of high-order approximations within methods. These high-order elements often involve formal accuracy that is much higher than the overall accuracy of the methods. For example a fourth-order approximation to the first derivative can be used to great effect with a method that only provides an overall second-order accuracy. With methods like PPM and FCT this can be taken to greater extremes. There one might use a fifth or sixth-order approximation for edge values even though the overall method is third order in one dimension or second-order in two or three dimensions. Another aspect of high order accuracy is better accuracy at local extrema. A usual approach to limiting to provide nonlinear stability clips extrema and computes them at first-order accuracy. In moving to limiters that do not clip extrema so harshly, excessive care must be taken so that the resulting method is not fragile and prone to oscillations. Alternatively, extrema-preserving methods can be developed that are relatively dissipative even compared to the better extrema clipping methods. Weighted ENO methods of almost any stripe are examples where the lack of extrema clipping is purchased at the cost of significant dissipation and relatively low overall computational fidelity. A better overall approach would be to use methods I have devised or the MP methods of Suresh and Huynh. Both of these methods are significantly more accurate than WENO methods.

One of the key points of this work is to make codes robust. Usually these techniques are originally devised as “kludges” that are crude and poorly justified. They have the virtue of working. The overall development effort is to guide these kludges into genuinely defensible methods, and then ultimately to algorithms. One threads the needle between robust solutions and technical rigor that lends confidence and faith in the simulation. The first rule is get an answer, then get a reasonable answer, then get an admissible answer, and then get an accurate answer. The challenges come through the systematic endeavor to solve problems of ever increasing difficulty and expand the capacity of simulations to address an ever-broader scope. We then balance this effort with the availability of knowledge to support the desired rigor. Our standards are arrived at philosophically through what constitutes an acceptable solution to our modeling problems.

Consistency and accuracy instills believability

― Bernard Kelvin Clive

Sweby, Peter K. “High resolution schemes using flux limiters for hyperbolic conservation laws.” SIAM journal on numerical analysis 21, no. 5 (1984): 995-1011.

Jiang, Guang-Shan, and Chi-Wang Shu. “Efficient implementation of weighted ENO schemes.” Journal of computational physics 126, no. 1 (1996): 202-228.

Colella, Phillip, and Paul R. Woodward. “The piecewise parabolic method (PPM) for gas-dynamical simulations.” Journal of computational physics 54, no. 1 (1984): 174-201.

Colella, Phillip. “A direct Eulerian MUSCL scheme for gas dynamics.” SIAM Journal on Scientific and Statistical Computing 6, no. 1 (1985): 104-117.

Bell, John B., Phillip Colella, and John A. Trangenstein. “Higher order Godunov methods for general systems of hyperbolic conservation laws.” Journal of Computational Physics 82, no. 2 (1989): 362-397.

Zalesak, Steven T. “Fully multidimensional flux-corrected transport algorithms for fluids.” Journal of computational physics 31, no. 3 (1979): 335-362.

Zalesak, Steven T. “The design of Flux-Corrected Transport (FCT) algorithms for structured grids.” In Flux-Corrected Transport, pp. 23-65. Springer Netherlands, 2012.

Quirk, James J. “A contribution to the great Riemann solver debate.” International Journal for Numerical Methods in Fluids 18, no. 6 (1994): 555-574.

Woodward, Paul, and Phillip Colella. “The numerical simulation of two-dimensional fluid flow with strong shocks.” Journal of computational physics 54, no. 1 (1984): 115-173.

Abgrall, Rémi, and Smadar Karni. “Computations of compressible multifluids.” Journal of computational physics 169, no. 2 (2001): 594-623.

Osher, Stanley. “Riemann solvers, the entropy condition, and difference.” SIAM Journal on Numerical Analysis 21, no. 2 (1984): 217-235.

Suresh, A., and H. T. Huynh. “Accurate monotonicity-preserving schemes with Runge–Kutta time stepping.” Journal of Computational Physics 136, no. 1 (1997): 83-99.

Rider, William J., Jeffrey A. Greenough, and James R. Kamm. “Accurate monotonicity-and extrema-preserving methods through adaptive nonlinear hybridizations.” Journal of Computational Physics 225, no. 2 (2007): 1827-1848.

 

 

The mystery of human existence lies not in just staying alive, but in finding something to live for.

― Fyodor Dostoyevsky

There is little doubt that we are living through monumental times in the history of humanity. I was born the child of the Cold War seeing that conflict end as I transitioned to adulthood and my professional life then seeing the birth of globalism powered by technology and communication unthinkable a generation before. My chosen profession looks increasingly like a relic of that Cold War, and increasingly irrelevant to the World that unfolds before me. My workplace is failing to keep pace with change, and I’m seeing it fall behind modernity in almost every respect. It’s a safe, secure job, but lacks most of the edge the real World offers. All of the forces unleashed in today’s World make for incredible excitement, possibility, incredible terror and discomfort. The potential for humanity is phenomenal, and the risks are profound. In short, we live in simultaneously in incredibly exciting and massively sucky times. Yes, both of these seemingly conflicting things can be true.

We are seeing a massive collision of the past and future across the globe pitting the forces of stability and progress against each other. We see the political power of conservative, anti-progress forces gaining the upper hand recently. The resurgent right wing seeks to push back against the changes pushed by demographics and empowered by technology. The reinvigorated tendency to use bigotry, hate and violence increasingly in a state-sponsored way is increasing. The violence against change is growing whether it is by governments or terrorists. What isn’t commonly appreciated is the alliance in violence of the right wing and terrorists. Both are fighting against the sorts of changes modernity is bringing. The fight against terror is giving the violent right wing more power. The right wing and Islamic terrorists have the same aim, undoing the push toward progress with modern views of race, religion and morality. The only difference is the name of the prophet the violence is done in name of.

This unholy alliance draws its power from the bookends of society. On one hand you have the poorer, uneducated masses of the population, and on the other you have the entrenched interests of the rich and powerful. The poor and uneducated are not able to manage the changes in society and want the brakes put on progress. The rich and powerful like the status quo and fear progress because it might not favor them as well. Together they ally against the middle class, who stands to benefit the most from progress. The alliance empowers violence among the poor, grows their ranks through polices that favor the wealthy. We see this happening across the globe where right wing, racist, Nationalist, overtly religious movements are attacking any societal progress. The rich and powerful pull the strings for their own purposes, enhancing their power and wealth at the expense of society as a whole.

The most insidious force of this unhealthy alliance is terrorism. The right wing wants to fight terrorism through enhancing the police-National-security state, which provides the rich and powerful the tools to control their societies as well. They also wage war against the sources of terrorism creating the conditions and recruiting for more terrorists. The police states have reduced freedom and lots of censorship, imprisonment, and opposition to personal empowerment. The same police states are effective at repressing minority groups within nations using the weapons gained to fight terror. Together these all help the cause of the right wing in blunting progress. The two allies like to kill each other too, but the forces of hate; fear and doubt work to their greater ends. In fighting terrorism we are giving them exactly what they want, the reduction of our freedom and progress. This is also the aim of right wing; stop the frightening future from arriving through the imposition of traditional values. This is exactly what the religious extremists want be they Islamic or Christian.

Driving the conservatives to such heights of violence and fear are changes to society of massive scale. Demographics are driving the changes with people of color becoming impossible to ignore, along with an aging population. Sexual freedom has emboldened people to break free of traditional boundaries of behavior, gender and relationships. Technology is accelerating the change and empowering people in amazing ways. All of this terrifies many people and provides extremists with the sort of alarmist rhetoric needed to grab power. We see these forces rushing headlong toward each other with society-wide conflict the impact. Progressive and conservative blocks are headed toward a massive fight. This also lines up along urban and rural lines, young and old, educated and uneducated. The future hangs in the balance and it is not clear who has the advantage.

The purpose of life is to contribute in some way to making things better.

― Robert F. Kennedy

The cell phone becoming a platform for communication and commerce at a scale unimaginable a decade ago has transformed the economics of the World. People are now connected globally through the cell phone, and these mini-computers allow new models of economic activity to sprout up constantly. The changes to how we live are incalculable with the cell phone shaping both our social and economic structures in deep and unforeseen ways. The social order is being shaped by the ability to connect to people in deeply personal ways without the necessity of proximity. We meet people online now and form relationships without ever meeting physically. Often people have had ongoing relationships with people they’ve never met or met rarely. They can maintain communication via text, audio or video with amazing ease. This starts to form different communities and relationships that are shaking culture. It’s mostly a middle class phenomenon and thus the poor are left out, and afraid.

The way we live, work, sleep, eat, and relate to each other has transformed completely in a decade. The balance of personal empowerment and threat to privacy sits at the precipice. The cell phone has made the Internet personal and ubiquitous redefining our social order. This excites people like me, and scares the shit out of others. We are seeing a change in our society at a pace unseen in the course of history. Violence is a likely result of the pace and intensity of this change. Economic displacements are accelerating, and our standard systems are poor at coping with everything. Everything from schools too many employers are incapable of evolving fast enough to benefit from the change. I perfect example are institutions like I work for. Despite being high tech and full of educated people, it is conservative, rule following, compliant, security conscious (too a paranoid level) and obsessively bureaucratic, largely incapable of adopting technology or taking risks with anything. My level of frustration is growing with each passing day. I’m seeing modernity pull ahead of me in the workplace due to fear and incompetence.

For example in my public life, I am not willing to give up the progress, and feel that the right wing is agitating to push the clock back. The right wing feels the changes are immoral and frightening and want to take freedom away. They will do it in the name of fighting terrorism while clutching the mantle of white nationalism and the Bible in the other hand. Similar mixes are present in Europe, Russia, and remarkably across the Arab world. My work World is increasingly allied with the forces against progress. I see a deep break in the not to distant future where the progress scientific research depends upon will be utterly incongruent with the values of my security-obsessed work place. The two things cannot live together effectively and ultimately the work will be undone by its inability to commit itself to being part of the modern World. The forces of progress are powerful and seemingly unstoppable too. We are seeing the unstoppable force of progress meet the immovable object of fear and oppression. It is going to be violent and sudden. My belief in progress is steadfast, and unwavering. Nonetheless, we have had episodes in human history where progress was stopped. Anyone heard of the dark ages? It can happen.

We’ll be remembered more for what we destroy than what we create.

― Chuck Palahniuk

I’ve been trying to come to grips with the changes in where I work. My workplace is adapting too slowing to modern life, and the meaning in work has become difficult to square with realities. The sense that my work doesn’t matter anymore has become increasingly palpable. I’ve gone from working for a clear sense of purpose and importance to a job that increasingly seethes with irrelevance. Every action from my masters communicates the lack of value of my work. Creating a productive and efficient workplace is never-ever important. We increasingly have no sense of importance in our work. This is delivered with disempowering edicts and policies that conspire to shackle me, and keep me from doing anything. The real message is that nothing you do is important enough to risk fucking up. I’m convinced that the things making work suck are strongly connected to everything else.

With each passing day the nature and forces at work and the rest of my life become more separate. It becomes hard to feel like I’m making the best, most productive use of my time and effort in work when I know so much effective productive effort is being left behind. The motives and rules of my employer are focused on safety and security above all else. Everything that makes modern life tick makes them uncomfortable. In addition things are evolving so fast for technology that organizations like mine cannot keep up. I can adapt quickly and learn, but if I do my desires and knowledge will become a source of tension rather than an advantage. If I keep up with technology I am more likely to be frustrated than productive. This is already happening and it is driving me up the wall.

The problem many organizations (companies, universities, Laboratories) are that they are large and move slowly. With a pace of change that is large by any historical standard, they don’t keep up or adapt. You get into a position where the organization is falling behind, and the forces of fear and hesitation are deadly. Add in a government who supplies the funding with rules galore and strings attached and you have the recipe for falling behind. Unless the organization, its leadership, and its people commit to adapting and pushing themselves forward, the organization will stagnate or be left behind by the exciting innovations shaping the World today. When the motivation of the organization fails to emphasize productivity and efficiency, the recipe is disastrous. Modern technology offers the potential for incredible advances, but only if they’re seeking advantage. If minds are not open to making things better, it is a recipe for frustration.

This ends up being a microcosm of today’s World. Modern advances in technology or society offer tremendous advantages for those willing to be bold, but they come with risk and discomfort. Many are deeply tied to the past and the old way of doing things along with old-fashioned sense of purpose. There is an inability or unwillingness to accept the potential of the modern. Without bold and willing endeavor, the new World passes organization by. This is where I feel the greatest pain, the passive manner in which the modern World passes my organization by. It is not unlike the broader social themes of those who accept the modern World, and the conservative resistance to everything. Organizations who fail to embrace the potential of the modern world unwittingly enter into the opposition to change, and assist the conservative attempt to hold onto the past.

The question to ask is whether these organization whose history and greatness are grounded in a time gone by can evolve into something modern. Do these organizations even want to change? Can they make the change even if they want to while tethered to the past? For those of us who are part of publically focused organizations, we are caught in between the forces raging politically. The institutions of government will almost certainly resist and avoid change. The result will be a slow decline and almost certain death for these organizations as the World changes. The alternative is the World not changing and progress stopping, this outcome is certainly worse for humanity.

History is always written by the winners. When two cultures clash, the loser is obliterated, and the winner writes the history books-books which glorify their own cause and disparage the conquered foe. As Napoleon once said, ‘What is history, but a fable agreed upon?

― Dan Brown

 

The possession of knowledge does not kill the sense of wonder and mystery. There is always more mystery.

― Anaïs Nin

Let’s say you’ve completely bought into my advice and decide to test the hell out of your code. You found some really good problems that “go to eleven.” If you do things right, your code will eventually “break” in some way. The closer you look, the more likely it’ll be broken. Heck your code is probably already broken, and you just don’t know it! Once it’s broken, what should you do? How do you get the code back into working order? What can you do to figure out why it’s broken? How do you live with the knowledge of the limitations of the code? Those limitations are there, but usually you don’t know them very well. Essentially you’ve gone about the process of turning over rocks with your code until you find something awfully dirty-creepy crawly underneath. You then have mystery to solve, and/or ambiguity to live with from the results.

An expert is someone who knows some of the worst mistakes that can be made in his subject, and how to avoid them.

― Werner Heisenberg

I’ll deal with the last question first, how to live with the knowledge of limitations. This is a sort of advice to grow up, and be an adult about things. Any method or code is going to be limited in what it can do. Some of these limitations are imposed by theory, or by practicality, or expense, some of the limitations simply get at the limits of our knowledge and technology today. One of the keys to being an expert in a given field is a deep

understanding of what can and cannot be done, and why. What better way of becoming an expert than purposefully making “mistakes?” Do you understand what the state of the art is? Do you know what is challenging to the state of the art? What are the limits imposed by theory? What do other people do to solve problems and what are the pros and cons to their approach? Exploring these questions, and stepping well outside the confines of comfort provided by success drive a deep knowledge of all of these considerations. When properly applied the art of testing codes delves into a deep knowledge of failures as the fuel for learning and the acquisition of knowledge.

So how might you see your code break? In the worst case the problem might induce an outright instability and the code will blow up. Sometimes the blow up will happen through the production of wild solutions, or even violations of the floating number limits of the computer (NaN’s or not a number will appear in output). Other problems look like corrupted data where the solution doesn’t blow up, but the solution is clearly very wrong. Moving down the chain of bad things we might simply see solutions outside the bounds of what is reasonable or admissible for valid solutions. As we walk through this gallery of bad things each succeeding step is subtler than the last. In our approach to breakage, an analytical solution to a problem can prove invaluable because it provides an unambiguous standard for the solution that can be as accurate as you please.

Next, we simply see solutions that are oscillatory or wiggly. These wiggles can go all the way from dangerous to cosmetic in their character. Sometimes the wiggles might interact with genuinely physical features in a model, and the imperfection is a real modeling problem. Next, we get into the real weeds of solution problems, and start to see failures that can go unnoticed without expert attention. One of the key things is the loss of accuracy in a solution. This could be the numerical level of error being wrong, or the rate of convergence of the solution being outside the theoretical guarantees for the method (convergence rates are a function of the method and the nature of the solution itself). Sometimes this character is associated with an overly dissipative solution where numerical dissipation is too large to be tolerated. At this subtle level we are judging failure by a high standard based on knowledge and expectations driven by deep theoretical understanding. These failings generally indicate you are at a good level of testing and quality.

Once the code is broken in some way, it is time to find out why. The obvious breakage where the solution simply falls apart is the best case to deal with because the failings are so obvious. The first thing you should always do is confirm that you’re solving the problem you think you are, and you’re solving it the way you think you are. This involves examining your input and control of the code to make certain that everything is what you expect it to be. Once you’re sure about this important detail, you can move to the sleuthing. For the obvious code breakdowns you might want to examine how the solution starts to fall apart as early in the process as you can. Is the problem localized near a boundary or a certain feature? Does it happen suddenly? Is there a slow, steady build up toward disaster? The answers all point at different sources for the problem. They tell how and where to look.

One of the key things to understand with any failure is the stability of the code and its methods. You should be intimately familiar with the conditions for stability for the code’s methods. You should assure that the stability conditions are not being exceeded. If a stability condition is missed, or calculated incorrectly, the impact is usually immediate and catastrophic. One way to do this on the cheap is modify the code’s stability condition to a more conservative version usually with a smaller safety factor. If the catastrophic behavior goes away then it points a finger at the stability condition with some certainty. Either the method is wrong, or not coded correctly, or you don’t really understand the stability condition properly. It is important to figure out which of these possibilities you’re subject to. Sometimes this needs to be studied using analytical techniques to examine the stability theoretically.

One of the key things to understand extremely well is the state of the art in a given field. Are there codes and methods that can solve the problem well or without problems? Nothing can replace an excellent working knowledge of what experts in the field are doing. The fastest way to solve a problem is understand and potentially adopt what the best and brightest are already doing. You also have a leg up on understanding what the limits of knowledge and technology are today, and whether you’ve kept up to the boundary of what we know. Maybe it is research to make you code functional, and if you fix it, you might have something publishable! If so, what do they do differently than your code? Can you modify how your code runs to replicate their techniques? If you can do this and reproduce the results that other are getting then you have a blueprint on how to fix your code.

Another approach to take is systematically make the problem you’re solving easier until the results are “correct,” or the catastrophic behavior is replaced with something less odious. An important part of this process is more deeply understand how the problems are being triggered in the code. What sort of condition is being exceeded and how are the methods in the code going south? Is there something explicit that can be done to change the methodology so that this doesn’t happen? Ultimately, the issue is a systematic understanding of how the code and its method’s behave, their strengths and weaknesses. Once the weakness is exposed in the testing can you do something to get rid of it? Whether the weakness is a bug or feature of the code is another question to answer. Through the process of successively harder problems one can make the code better and better until you’re at the limits of knowledge.

The foundation of data gathering is built on asking questions. Never limit the number of hows, whats, wheres, whens, whys and whos, as you are conducting an investigation. A good researcher knows that there will always be more questions than answers.

― Karl Pippart III

Whether you are at the limits of knowledge takes a good deal of experience and study. You need to know the field and your competition quite well. You need to be willing to borrow from others and consider their success carefully. There is little time for pride, if you want to get to the frontier of capability; you need to be brutal and focused along the path. You need to keep pushing your code with harder testing and not be satisfied with the quality. Eventually you will get to problems that cannot be overcome with what people know how to do. At that point your methodology probably needs to evolve a bit. This is really hard work, and prone to risk and failure. For this reason most codes never get to this level of endeavor, its simply too hard on the code developers, and worse on those managing them. Today’s management of science simply doesn’t enable the level of risk and failure necessary to get to the summit of our knowledge. Management wants sure results and cannot deal with ambiguity at all, and striving at the frontier of knowledge is full of it, and usually ends up failing.

The most beautiful experience we can have is the mysterious. It is the fundamental emotion that stands at the cradle of true art and true science.

― Albert Einstein

At the point you meet the frontier, it is time to be willing to experiment with your code (experimentation is great to do even safely within the boundaries of know how). Often the only path forward is changing the way you solve problems. One key is to not undo all the good things you can already do in the process. Quite often one might actually solve the hard problem is some way (like a kludge), only to find out that things that used to be correct and routine for easier problems have been wrecked in the process. That is a back to the drawing board moment! For the very hard problem you may simply be seeking robustness and stability (running the problem to completion), and the measures taken to achieve this do real damage to your bread and butter. You need to be prepared to instrument and study your output in new ways. You are now an explorer, and innovator. Sometimes you need to tackle the problem from a different perspective, challenge your underlying beliefs and philosophies.

The true measure of success is how many times you can bounce back from failure.

― Stephen Richards

At this point its useful to point out that the literature is really bad at documenting what we don’t know. Quite often you are rediscovering something lots of experts already know, but can’t publish. This is one of the worst things about the publishing of research, we really only publish success, and not failure. As a result we have a very poor idea of what we can’t do. It’s only available through inference. Occasionally the state of what can’t be done is published, but usually not. What you may not realize that you are crafting a lens on the problem and a perspective that will shape how you try to solve it. This process is a wonderful learning opportunity and the essence of research. For all these reasons it is very hard and almost entirely unsupportable.

Another big issue is finding general purpose fixes for hard problems. Often the fix to a really difficult problem wrecks your ability to solve lots of other problems. Tailoring the solution to treat the difficulty and not destroy the ability to solve other easier problems is an art and the core of the difficulty in advancing the state of the art. The skill to do this requires fairly deep theoretical knowledge of a field study, along with exquisite understanding of the root of difficulties. The difficulty people don’t talk about is the willingness to attack the edge of knowledge and explicitly admit the limitations of what is currently done. This is an admission of weakness that our system doesn’t support. When fixes aren’t general purpose, one clear sign is a narrow range of applicability. If its not general purpose and makes a mess of existing methodology, you probably don’t really understand what’s going on.

Let’s get to a general theme in fixing problems, add some dissipation to stabilize things and get rid of worrisome features. In the process you often end up destroying the very features of the solution you most want to produce. The key is to identify the bad stuff and keep the good stuff, and this comes from a deep understanding plus some vigorous testing. Dissipation almost always results in a more robust code, but the dissipation needs to be selective, or the solution is arrived at in a wasteful manner. As one goes even deeper into the use of dissipation, the adherence to the second law of thermodynamics rears its head, and defines a tool of immense power if wielded appropriately. A key is to use deep principles to achieve a balanced perspective on dissipation where it is used appropriately in clearly defensible, but limited ways. Even today applying dissipation is still an art, and we struggle to bring more science and principle to its application.

I’ve presented a personally biased view of how to engage in this sort of work. I’m sure other fields will have similar, but different rules for engaging in fixing codes. The important thing is putting simulation codes to the sternest tests they can take, exposing their weaknesses and repairing them. One wants to continually do this until you hit the proverbial wall of our knowledge and ability. Along the way you create a better code, learn the field of endeavor and grow the knowledge and capability of yourself. Eventually the endeavor leads to research and the ability to push the field ahead. This is also the way of creating experts, and masters of a given field. People move from simply being competent practitioners to masters and leaders. This is an unabashed good for everyone, and not nearly encouraged enough. It definitely paves the way forward and produces exceptional results.

A pessimist sees the difficulty in every opportunity; an optimist sees the opportunity in every difficulty.

― Winston S. Churchill

 

or the alternative title “These Problems go to Eleven!”

Fortunate are those who take the first steps.

― Paulo Coelho

When thinking about problems to run with a computer code there is both a fun and a harsh way to think about them. I’ll start with the fun way, borrowing from the brilliant movie “This is Spinal Tap” and the hilarious interview with the lead guitarist from the band,

Nigel Tufnel: The numbers all go to eleven. Look, right across the board, eleven, eleven, eleven and…

Marty DiBergi: Oh, I see. And most amps go up to ten?

Nigel Tufnel: Exactly.

Marty DiBergi: Does that mean it’s louder? Is it any louder?

Nigel Tufnel: Well, it’s one louder, isn’t it? It’s not ten. You see, most blokes, you know, will be playing at ten. You’re on ten here, all the way up, all the way up, all the way up, you’re on ten on your guitar. Where can you go from there? Where?

Marty DiBergi: I don’t know.

Nigel Tufnel: Nowhere. Exactly. What we do is, if we need that extra push over the cliff, you know what we do?

Marty DiBergi: Put it up to eleven.

Nigel Tufnel: Eleven. Exactly. One louder.

Marty DiBergi: Why don’t you make ten a little louder, make that the top number and make that a little louder?

Nigel Tufnel: [pauses] These go to eleven.

To make the best progress we need to look for problems that “go to eleven.” Even if the difficulty is somewhat artificial, the best problems are willfully extreme, if not genuinely silly. They expose the mechanisms that break methods. Often these problems are simplified versions of what we know brings the code to its knees, and serve as good blueprints for removing these issues from the code’s methods. Alternatively, they provide proof that certain pathological behaviors do or don’t exist in a code. Really brutal problems that “go to eleven” aid the development of methods by highlighting where improvement is needed clearly. Usually the simpler and cleaner problems are better because more codes and methods can run them, analysis is easier and we can successfully experiment with remedial measures. This allows more experimentation and attempts to solve it using diverse approaches. This can energize rapid progress and deeper understanding.

The greater the obstacle, the more glory in overcoming it.

― Molière

I am a deep believer in the power of brutality at least when it comes to simulation codes. I am a deep believer that we are generally too easy on our computer codes; we should endeavor to break them early and often. A method or code is never “good enough”. The best way to break our codes is attempt to solve really hard problems that are beyond our ability to solve today. Once the solution of these brutal problems is well enough in hand, one should find a way of making the problem a little bit harder. The testing should actually be more extreme and difficult than anything we need to do with codes. One should always be working at, or beyond the edge of what can be done instead of safely staying within our capabilities. Today we are too prone to simply solving problems that are well in hand instead of pushing ourselves into the unknown. This tendency is harming progress.

Stark truth, is seldom met with open arms.

― Justin K. McFarlane Beau

Easy problems make codes look good because they don’t push the boundaries. Easy problems are important for checking the code’s ability to be correct and work when everything is going right. The codes need to continue working when everything is going wrong too. A robust code is functional under the worst of circumstances one might encounter. The brutal problems are good at exposing many of the conditions where things go wrong, and pushing the codes to be genuinely robust. These conditions almost invariably appear in real problems, and good codes can navigate the difficulties without falling apart. Over time good codes can go from falling apart to solving these brutal problems accurately. When this happens we need to come up with new problems to brutalize the codes. We should always be working on the edge or over the edge of what is possible; safe and sound is no way to make things better.

Happiness is not the absence of problems; it’s the ability to deal with them.

― Steve Maraboli

The use of brutal problems has helped drive codes forward for decades. A long time ago simple problems that we routinely solve today brought codes to their collective knees. Examples of such problems for shock physics codes are the Sedov-Taylor blast wave and Noh’s problem. Scientists came up with new ways to solve problems that brought these problems to heel. Rather than rest upon our laurels, we found new problems to bring the codes down. We still solve the older, now tamed brutal problems, but now they are easy. Once we slay one dragon, it is time to construct a bigger, more dangerous dragon to do battle with. We should always test our mettle against a worthy opponent rather than matching up with a patsy. Getting fabulous results on a super-easy problem looks great, but does little or nothing to improve us. Through this process we progress and our codes get better and better. This is how we challenge ourselves systematically always working with the premise that we can improve and get better. Brutal problems provide a concrete focus for improvement.

A challenge only becomes an obstacle when you bow to it.

― Ray A. Davis

What does this process look like concretely? We have problems that used to push the boundaries of our ability such as the Sod shock tube. It used to be a problem we couldn’t solve well. Shock tube problems have the added benefit of having exact solutions (Noh and Sedov-Taylor do too), so agreement and error have little to no ambiguity. Solutions either had oscillations or they were inaccurate and very heavily diffused. Often important features in the solution were seriously corrupted. This problem appeared in the literature at a seminal time in the development of numerical methods for shock physics and offered a standard way of testing and presenting results.

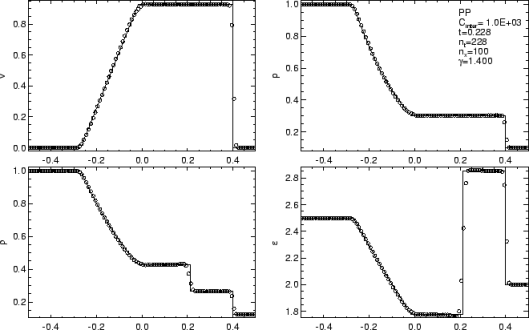By the time a decade had passed after the introduction of Sod’s problem almost all of the pathological solutions we used to see had disappeared and far better methods existed (not because of Sod’s problem per se, but something was “in the air” too). The existence of a common problem to test and present results was a vehicle for the community to use in this endeavor. Today, the Sod problem is simply a “hello World” for shock physics and offers no real challenge to a serious method or code. It is difficult to distinguish between very good and OK solutions with results. Being able to solve the Sod problem doesn’t really qualify you to attack really hard problems either. It is a fine opening ante, but never the final call. The only problem with using the Sod problem today is that too many methods and codes stop their testing there and never move to the problems that challenge our knowledge and capability today. A key to making progress is to find problems where things don’t work so well, focus attention on changing that.

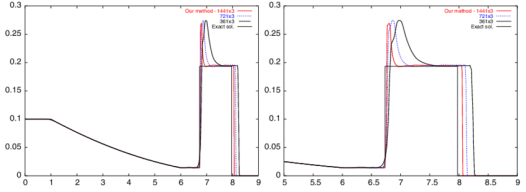Therefore, if we want problems to spur progress and shed light on what works, we need harder problems. For example, we could systematically up the magnitude of the variation in initial conditions in shock tube problems until results start to show issues. This usefully produces harder problems, but really hasn’t been done (note to self this is a really good idea). One problem that produces this comes from the National Lab community in the form of LeBlanc’s shock tube, or its more colorful colloquial name, “the shock tube from Hell.” This is a much less forgiving problem than Sod’s shock tube, and that is an understatement. Rather than jumps in pressure and density of about one order of magnitude, the jump in density is 1000-to-1 and the jump in pressure is one billion-to-one. This stresses methods far more than Sod and many simple methods can completely fail. Most industrial or production quality methods can actually solve the problem albeit with much more resolution than Sod’s problem requires (I’ve gotten decent results on Sod’s problem on mesh sequences of 4-8-16 cells!). For the most part we can solve LeBlanc’s problem capably today, so its time to look for fresh challenges.

One such challenge is posed by problems with void in them, or those that dynamically produce vacuum conditions. We have found that this class of problems simply is not solved effectively with current methods. Every method I’ve looked at fails in some way shape or form. None of them converge to the correct solution once the problem gets close enough to vacuum or void conditions. The only methods that appear to work at all explicitly track the position of the vacuum, so my statement of dysfunction should be applied to shock capturing methods. It does not seem to be a well-appreciated or well-studied problem thus may be ripe for the picking. Running this problem and focusing on results would provide impetus for improving this clearly poor state of affairs.

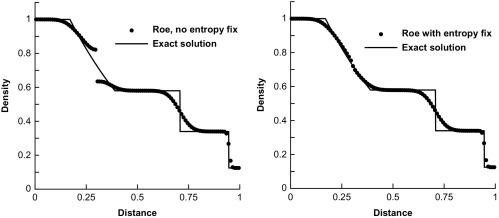Other good problems are devised though knowing what goes wrong in practical calculation. Often those who know how to solve the problem create these problems. A good example is the issue of expansion shocks, which can be seen by taking Sod’s shock tube and introducing a velocity to the initial condition. This puts a sonic point (where the characteristic speed goes to zero) in the rarefaction. We know how to remove this problem by adding an “entropy” fix to the Riemann solver defining a class of methods that work. The test simply unveils whether the problem infests a code that may have ignored this issue. This detection is a very good side-effect of a well-designed test problem.

Another great example is the carbuncle instability where mesh aligned shock wave exhibit and symmetry breaking bounded instability. This problem was seen first in blunt body simulation of re-entry vehicles, but inhabits frightfully many simulations in a host of applications. The issue still remains inadequately solved although some remedies exist, none is fully satisfactory. The progress made to date has largely arisen through its more clear identification and the production of simplified test problems that exhibit its fundamental behavior. In my own experience if a code doesn’t explicitly stabilize the carbuncle instabilities, the problem will be present and manifest itself. These manifestations will often be subtle and difficult to detect often masquerading as valid physical effects. A good test problem will expose the difficulty and force the code to be robust to it.

One of the best carbuncle exposing problems simply propagates a strong shock wave in one dimension, hardly a challenge today. The wrinkle in the problem is to make the problem two or three dimensional even though the extra dimensions should be ignorable. It introduces a small perturbation to the problem and tests whether the shock wave induces an unphysical growth in the resulting solution. Codes that exhibit the carbuncle instability allow the perturbations to grow and ultimately corrupt the solution. The problem is simple and elegant, but brutally effective for the purpose it was designed. It was inspired by the path to successful analysis of the core issues leading to the carbuncle instability.

The key idea to the modeling and simulation enterprise is identifying problems that expose weaknesses in current methods and codes. Once these weaknesses are addressed they provide a codec of wisdom about problems that have solved, and whether such wisdom was accounted for in a new method or code. New problems working at the boundaries of our knowledge are needed to push the community and spur progress. Meaningful progress can be measured through the conversion of such challenging problems from those that break methods and codes, to reasonable solution by methods and codes, and finally to accurate solution. When a problem has moved from a threat to success, it is time to create a new harder problem to continue progress.

Ultimately the brutal problems are an admission of where the method or code is vulnerable. This reflects on the personal vulnerability of those who professionally associated themselves with the code. This makes testing the code rigorously and brutally impossibly hard especially in today’s “no failure allowed” accountability culture. Its much easier to simply stop where everything appears to work just fine. Brutal problems spur growth, but also challenge our belief of mastery and success. It takes strong people to continually confront the boundaries of their knowledge and capability push it back, and confront it anew over and over.

At a deeply personal level testing codes becomes an exercise in leaving one’s comfort zone. The comfort zone is where you know how to solve problems, and you feel like you have mastery of things. Breaking your code, fixing it and breaking it again is a process of stepping out of the comfort zone as a principle in energizing progress. In my experience we have a culture that increasingly cannot deal with failure successfully. We must always succeed and get punished mercilessly for failure. Risk must be identified and avoided at all costs. The comfort zone is success, and for codes this looks like successful operation, and bona fide healthy convergence all of which is provided by easy problems. Brutal problems expose not just code weaknesses, but personal weakness and intellectual failings or gaps. Rather than chase personal excellence we are driven to choose comfortable acquiescence to the status quo. Rather than be vulnerable and admit our limitations, we choose comfort and false confidence.

Vulnerability is the birthplace of love, belonging, joy, courage, empathy, and creativity. It is the source of hope, empathy, accountability, and authenticity. If we want greater clarity in our purpose or deeper and more meaningful spiritual lives, vulnerability is the path.

― Brené Brown

Sod, Gary A. “A survey of several finite difference methods for systems of nonlinear hyperbolic conservation laws.” Journal of computational physics 27, no. 1 (1978): 1-31.

Pember, R. B., and R. W. Anderson. A Comparison of Staggered-Mesh Lagrange Plus Remap and Cell-Centered Direct Eulerian Godunov Schemes for Rulerian Shock Hydrodynamics. No. UCRL-JC-139820. Lawrence Livermore National Lab., CA (US), 2000.

Gottlieb, J. J., and C. P. T. Groth. “Assessment of Riemann solvers for unsteady one-dimensional inviscid flows of perfect gases.” Journal of Computational Physics 78, no. 2 (1988): 437-458.

Munz, C‐D. “A tracking method for gas flow into vacuum based on the vacuum Riemann problem.” Mathematical methods in the applied sciences 17, no. 8 (1994): 597-612.

Quirk, James J. “A contribution to the great Riemann solver debate.” In Upwind and High-Resolution Schemes, pp. 550-569. Springer Berlin Heidelberg, 1997.