Not trying or putting forth your best effort is.

Only those who dare to fail greatly can ever achieve greatly.

― Robert F. Kennedy

Last week I attended the ASME Verification and Validation Symposium as I have for the last five years. One of the keynote talks ended with a discussion of the context of results in V&V. It used the following labels for an axis: Success (good) and Failure (bad). I took issue with it, and made a fairly controversial statement. Failure is not negative or bad, and we should not keep referring to it as being negative. I might even go so far as to suggest that we actually encourage failure, or at the very least celebrate it because failure also implies your trying. I would be much happier if the scale was related to effort and excellence of work. The greatest sin is not failing; it is not trying.

Keep trying; success is hard won through much failure.

― Ken Poirot

It is actually worse than simply being a problem that the best effort isn’t put forth, lack of acceptance of failure inhibits success. The outright acceptance of failure as a viable outcome of work is necessary for the sort of success one can have pride in. If nothing is risked enough to potentially fail than nothing can be achieved. Today we have accepted the absence of failure as being the tell tale sign of success. It is not. This connection is desperately unhealthy and leads to a diminishing return on effort. Potential failure while an unpleasant prospect is absolutely necessary for achievement. As such the failures when best effort is put forth should be celebrated and lauded whenever possible and encouraged. Instead we have a culture that crucifies those who fail with regard for the effort on excellence of the work going into it.

Right now we are suffering in many endeavors from deep unremitting fear of failure. The outright fear of failing and the consequences of that failure are resulting in many efforts reducing their aggressiveness in attacking their goals. We reset our goals downward to avoid any possibility of being regarded as failing. The result is an extensive reduction in achievement. We achieve less because we are so afraid of failing at anything. This is resulting is the destruction of careers, and the squandering of vast sums of money. We are committing to mediocre work that is guaranteed of “success” rather than attempting excellent work that could fail.

A person who never made a mistake, never tried anything new

― Albert Einstein

We have not recognized the extent to which failure energizes our ability to learn, and bootstrap ourselves to a greater level of achievement. Failure is perhaps the greatest means to teach us powerful lessons. Failure is a means to define our limits of understanding and knowledge. Failure is the fuel for discovery. Where we fail, we have work that needs to be done. We have mystery and challenge. Without failure we lose discovery, mystery, challenge and understanding. Our knowledge becomes stagnant and we cease learning. We should be embracing failure because failure leads to growth and achievement.

Instead today we recoil and run from failure. Failure has become such a massive black mark professionally that people simply will not associate themselves with something that isn’t a sure thing. The problem is that sure things aren’t research they are developed science and technology. If one is engaged in research, we do not have certain results. The promise of discovery is also tinged with the possibility of failure. Without the possibility of failure, discovery is not possible. Without an outright tolerance for a failed result or idea, the discovery of something new and wonderful cannot be had. At a personal level the ability to learn, develop and master knowledge is driven by failure. The greatest and most compelling lessons in life are all driven by failures. With a failure you learn a lesson that sticks with you, and your learning sticks.

Creatives fail and the really good ones fail often.

― Steven Kotler

It is the ability to tolerate ambiguity in results that leads to much of the management response. Management is based on assuring results and defining success. Our modern management culture seems to be incapable of tolerating the prospect of failure. Of course the differences in failure are not readily supported by our systems today. There is a difference between an earnest effort that still fails and an incompetent effort that fails. One should be supported and celebrated and the other is the definition of unsuccessful. We have lost the capacity to tolerate these subtleties. All failure is viewed as the same and management is intolerant. They require results that can be predicted and failure undermines this central tenant of management.

The end result of all of this failure avoidance is a generically misplaced sense of what constitutes achievement. More deeply we are losing the capacity to fully understand how to structure work so that things of consequence may be achieved. In the process we are wasting money, careers and lives in the pursuit of hollowed out victories. The lack of failure is now celebrated even though the level of success and achievement is a mere shadow of the sorts of success we saw a mere generation ago. We have become so completely under the spell of avoidance of scandal that we shy away from doing anything bold or visionary.

A Transportation Security Administration (TSA) officer pats down Elliott Erwitt as he works his way through security at San Francisco International Airport in San Francisco, Wednesday, Nov. 24, 2010. (AP Photo/Jeff Chiu)

We live in an age where the system cannot tolerate a single bad event (e.g., failure whether it is an engineered system, or a security system,…). In the real World failures are utterly and completely unavoidable. There is a price to be paid for reductions of bad events and one can never have an absolute guarantee. The cost of reducing the probability of bad events escalates rather dramatically as you look to reduce the tail probabilities beyond a certain point. Things like the mass media and demagoguery by politicians takes any bad event and stokes fears using the public’s response as a tool for their own power and purposes. We are shamelessly manipulated to be terrified of things that have always been one-off minor risks to our lives. Our legal system does its dead level best to amp all of this fearful behavior for their own selfish interests of siphoning as much money as possible from whoever has the misfortune of tapping into the tails of extreme events.

In the area of security, the lack of tolerance for bad events is immense. More than this, the pervasive security apparatus produces a side effect that greatly empowers things like terrorism. Terror’s greatest weapon is not high explosives, but fear and we go out of our way to do terrorists jobs for them. Instead of tamping down fears our government and politicians go out of their way to scare the shit out of the public. This allows them to gain power and fund more activities to answer the security concerns of the scared shitless public. The best way to get rid of terror is to stop getting scared. The greatest weapon against terror is bravery, not bombs. A fearless public cannot be terrorized.

The end result of all of this risk intolerance is a lack of achievement as individuals, organizations, or the society itself. Without the acceptance of failure, we relegate ourselves to a complete lack of achievement. Without the ability to risk greatly we lack the ability to achieve greatly. Risk, danger and failure all improve our lives in every respect. The dial is too turned away from accepting risk to allow us to be part of progress. All of us will live poorer lives with less knowledge, achievement and experience because of the attitudes that exist today. The deeper issue is that the lack of appetite for obvious risks and failure actually kicks the door open for even greater risks and more massive failures in the long run. These sorts of outcomes may already be upon us in terms of massive opportunity cost. Terrorism is something that has cost our society vast sums of money and undermined the full breadth of society. We should have had astronauts on Mars already, yet the reality of this is decades away, so our societal achievement is actually deeply pathetic. The gap between “what could be” and “what is” has grown into a yawning chasm. Somebody needs to lead with bravery and pragmatically take the leap over the edge to fill it.

We have nothing to fear but fear itself.

– Franklin D. Roosevelt.

Advances are made by answering questions. Discoveries are made by questioning answers. Bernard Haisch

― Philip Houston

In the constellation of numerical analysis theorems the Lax equivalence theorem may have no equals in its importance. It is simple and its impact is profound on the whole business of numerical approximations. The theorem basically implies that if you provide a consistent approximation to the differential equations of interest and it is stable, the solution will converge. The devil of course is in the details. Consistency is defined by having an approximation with ordered errors in the mesh or time discretization, which implies that the approximation is at least first-order accurate, if not better. A key aspect of this that is overlooked is the necessity to have mesh spacing sufficiently small to achieve the defined error where failure to do so renders the solution erratically convergent at best.

The importance of this theorem in the basis for our commitment to high performance computing cannot be understated. The generally implicit assumption that more computer power is the path to better calculation is incredibly widespread. The truth and limits of this assumption are important to understand. If things are working well, it is a good assumption, but it should not be taken for granted. A finer mesh is almost a priori assumed to be better. This basic premise is rarely if ever challenged, but it should be. Under ideal circumstances it is a fine assumption, but it is not challenged nearly as often as it should be. Part of this narrative is the description of when it should be challenged and the nature of circumstances where verification achieves outright conflict with the utility of the model. We end with the prospect that the verified model might only be accurate and verified in cases where the model is actually invalid.

For example we can carry out a purely mathematical investigation of the convergence of a numerical solution without any regard for its connection to a models utility. Thus we can solve a problem using time and length scales that would render the underlying model as ridiculous and satisfy the mathematical conditions we are examining. Stepping away from this limited perspective to look at the combination of convergence with model utility is necessary. In practical terms the numerical error and convergence where a model is valid is essentially important to understand. Ultimately we need accurate numerical solutions in regimes where a model is valid. More than just being accurate, we need to understand what the numerical errors are in these same regions. Too often we see meshes refined to a ridiculous degree without regard to whether the length scales in the mesh render the model invalid.

I have always thought the actions of men the best interpreters of their thoughts.

― John Locke

A second widespread and equally troubling perspective is the wrong-headed application of the concept of grid independent solutions. Achieving a grid-independent solution is generally viewed as a good to great thing. It is if the conditions are proper. It is not under almost identical conditions. The difference between the good almost great thing, and the awful almost horrible thing is a literal devil in the details, but essential to the conduct of excellence in computational science. One absolutely must engage in the quantitative interrogation of the results. Without a quantitative investigation, the good grid independent results could actually be an illusion.

If the calculation is convergent, the grid independence actually means the calculation is not sensitive to the grid in a substantive manner. This requires that the solution have small errors and the grid independence is the effect of those errors being ordered and negligible. In fact it probably means that you’re engaged in overkill and could get away with a coarser (cheaper) grid without creating any substantial side effects. On the other hand a grid independent solution could mean that the calculation is complete garbage numerically because the grid doesn’t affect the solution. It is not convergent. These two cases are virtually identical in practice and only revealed by doing detailed quantitative analysis of the results. In the end grid independence isn’t either necessary, or sufficient for quality computations. Yet at the same time it is often the advised course of action in conducting computations!

Stability then becomes the issue where you must assure that the approximations produce bounded results under the appropriate control of the solution. Usually the stability is defined as a character of the time stepping approach and requires that the time step be sufficiently small to provide stability. A lesser-known equivalence theorem is due to Dahlquist and applies to integrating ordinary differential equations and applies to multistep methods. From this work the whole aspect of zero stability arises where you have to assure that a non-zero time step size gives stability in the first place. More deeply, Dahlquist’s version of the equivalence theorem applies to nonlinear equations, but is limited to multistep methods where as Lax’s applies to linear equations.

Here is the theorem in all its glory (based on wikipedia entries).

The Lax Equivalence Theorem:

For the numerical solution of partial differential equations. It states that for a consistent finite difference method for a well-posed linear initial value problem, the method is convergent if and only if it is stable. Published in 1956, discussed in a seminar by Lax in 1954.

The Dahlquist Equivalence Theorem:

Now suppose that a consistent linear multistep method is applied to a sufficiently smooth differential equation and that the starting values  all converge to the initial value  as . Then, the numerical solution converges to the exact solution as  if and only if the method is zero-stable.

Something to take serious note of regarding these theorems is the concept of numerical stability was relatively new and novel in 1956. Both theorems helped to lock the concept of stability into being central to numerical analysis. As such both theorems have place as one of the cornerstones of modern numerical analysis. The discovery of the issue of stability was first addressed by Von Neumann for PDEs in the late 1940’s, and independently explored by Dahlquist for ODEs in the early 1950’s. Nonetheless it should be noted that these theorems were published when numerical stability was a new concept and not completely accepted and understood for its importance.

Given that we can very effectively solve nonlinear equations using the principles applied by Lax’s theorem is remarkable. Even though the theorem doesn’t formally apply to the nonlinear case the guidance is remarkably powerful and appropriate. We have a simple and limited theorem that produces incredible consequences for any approximation methodology that we are applying to partial differential equations. Moreover the whole this was derived in the early 1950’s and generally thought through even earlier. The theorem came to pass because we knew that approximations to PDEs and their solution on computers do work. Dahlquist’s work is founded on a similar path; the availability of the computers shows us what the possibilities are and the issues that must be elucidated. We do see a virtuous cycle where the availability of computing capability spurs on developments in theory. This is an important aspect of healthy science where different aspects of a given field push and pull each other. Today we are counting on hardware advances to push the field forward. We should be careful that our focus is set where advances are ripe, its my opinion that hardware isn’t it.

The equivalence theorem also figures prominently in the exercise of assuring solution quality through verification. This requires the theorem to be turned ever so slightly on its head in conducting the work. Consistency is not something that can be easily demonstrated; instead verification focuses on convergence, which may be. We can control the discretization parameters, mesh spacing or time step size to show how the solution changes with respect to them. Thus in verification, we use the apparent convergence of solutions to imply both stability and consistency. Stability is demonstrated by fiat in that we have a bounded solution to use to demonstrate convergence. Having a convergent solution with ordered errors then provides consistency. The whole thing barely hangs together, but makes for the essential practice in numerical analysis.

At this time we are starting to get at the practical limitations of this essential theorem. One way to get around the issues is the practice of hard-nosed code verification as a tool. With code verification you can establish that the code-discretization produces the correct solution to an exact solution to the PDEs. In this way the consistency of the approximation can become firmly established. Part of the remaining issue is the fact that the analytical exact solution is generally far nicer and better behaved that the general solutions you will be applying the code to. Still this is a vital and important step in the overall practice. Without firm code verification as a foundation, the practice of verification without exact solutions is simply untethered. Here we have firmly established the second major limitation of the equivalence theorem, the first being it’s being limited to linear equations.
One of the very large topics in V&V that is generally overlooked is models and their range of validity. All models are limited in terms of their range of applicability based on time and length scales. For some phenomena this is relatively obvious, e.g., multiphase flow. For other phenomena the range of applicability is much more subtle. Among the first important topics to examine is the satisfaction of the continuum hypothesis, the capacity of a homogenization or averaging to be representative. The degree of satisfaction of homogenization is dependent on the scale of the problem and degrades as phenomenon becomes smaller scale. For multiphase flow this is obvious as the example of bubbly flow shows. As the number of bubbles becomes smaller any averaging becomes highly problematic. It argues that the models should be modified in some fashion to account for the change in scale size.

I’ll get at another extreme example of the nature of scale size and the capacity of standard models to apply. Take the rather pervasive principle associated with the second law of thermodynamics. As the size of the system being averaged becomes smaller and smaller eventually violations of this law can be occasionally observed. This clearly means that natural and observable fluctuations may cause the macroscopic laws to be violated. The usual averaged continuum equations do not support this behavior. It would imply that the models should be modified for appropriate scale dependence where such violations in the fundamental laws might naturally appear in solutions.

Another more pernicious and difficult issues are homogenization assumptions that are not so fundamental. Consider the situation where a solid is being modeled in a continuum fashion. When the mesh is very large, the solid comprised of discrete grains can be modeled by averaging over these grains because there are so many of them. Over time we are able to solve problems with smaller and smaller mesh scales. Ultimately we now solve problems where the mesh size approaches the grain size. Clearly under this circumstance the homogenization used for averaging will lose its validity. The structural variations in the homogenized equations are removed and should become substantial and not be ignored as the mesh size becomes small. In the quest for exascale computing this issue is completely and utterly ignored. Some areas of study for high performance computing consider these issues carefully most notably climate and weather modeling where the mesh size issues are rather glaring. I would note that these fields are subjected to continual and rather public validation.

Let’s get to some other deeper limitations of the power of this theorem. For example the theorem gets applied to the models without any sense of the validity of the model. Without consideration for validity, the numerical exploration of convergence may be explored with vigor and be utterly meaningless. The notion of validation is important in considering whether verification should be explored in depth. As such one gets to the nature of V&V as holistic and iterative. As such the overall exploration should always look back at results to determine whether everything is consistent and complete. If the verification exercise takes the model outside its region of validity, the verification error estimation may be regarded as suspect.

The theorem is applied to the convergence of the model’s solution in the limit where the “mesh” spacing goes to zero. Models are always limited in their applicability as a function of length and time scale. The equivalence theorem will be applied and take many models outside their true applicability. An important thing to wrangle in the grand scheme of things is whether models are being solved and convergent in the actual range of scales where it is applicable. A true tragedy would be a model that is only accurate and convergent in regimes where it is not applicable. This may actually be the case in many cases most notably the aforementioned multiphase flow. This calls into question the nature of the modeling and numerical methods used to solve the equations.

Huge volumes of data may be compelling at first glance, but without an interpretive structure they are meaningless.

― Tom Boellstorff

The truth is we have an unhealthy addiction to high performance computing as a safe and trivial way to make progress computationally. We continually move forward with complete faith that a larger calculations are intrinsically better without doing the legwork to demonstrate that they are. We avoid focus on other routes to better solutions in modeling, methods and algorithms in favor of simply porting old models, methods and algorithms to much larger computers. Without having a balanced program with appropriate intellectual investment and ownership of the full breadth of computational science, our approach is headed for disaster. We have a significant risk of producing a computational science program that completely fools itself. We fail to do due diligence activities in favor of simply making the assumption that a finer mesh computed on bigger computers is a priori better than taking another route to improvement.

The difficulty lies not so much in developing new ideas as in escaping from old ones.

― John Maynard Keynes

Lax, Peter D., and Robert D. Richtmyer. “Survey of the stability of linear finite difference equations.” Communications on Pure and Applied Mathematics 9.2 (1956): 267-293.

Dahlquist, Germund. “Convergence and stability in the numerical integration of ordinary differential equations.” Mathematica Scandinavica 4 (1956): 33-53.

…fuck?

WTF has become the catchphrase for today’s world. “What the fuck” moments fill our days and nothing is more WTF than Donald Trump. We will be examining the viability of the reality show star, and general douchebag celebrity-rich guy as a viable presidential candidate for decades to come. Some view his success as a candidate apocalyptically, or characterize it as an “extinction level event” politically. In the current light it would seem to be a stunning indictment of our modern society. How could this happen? How could we have come to this moment as a nation where it is even a possibility for such a completely insane outcome to be a reasonably high probability outcome of our political process? What else does it say about us as a people? WTF? What in the actual fuck!

The phrase “what the fuck” came into the popular lexicon along with Tom Cruz in the movie, “Risky Business” back in 1983. There the lead character played by Tom Cruz exclaims, “sometimes you gotta say, what the fuck” It was a mantra for just going for broke and trying stuff without obvious regard for the consequences. Given our general lack of an appetite for risk and failure, the other side of the coin took the phrase over. Over time the phrase has morphed into a general commentary about things that are generally unbelievable. Accordingly the acronym WTF came into being by 1985. I hope that 2016 is peak-what the fuck, cause things can’t get much more what the fuck without everything turning into a complete shitshow. Going to a deeper view of things the real story behind where we are is the victory of bullshit as a narrative element in society. In a sense the transfer of WTF from a mantra for risk taking has transmogrified into a mantra for the breadth of impact of not taking risks!

Indeed if one looks to the real core of the Donald Trump phenomena it is the victory of bullshit over logic, facts and rational thought. He simply spouts off a bunch of stuff that our generally uneducated, bigoted, and irrationally biased public wants to hear, and the rubes vote for him in droves. It does not matter that almost everything he says is complete and utter bullshit. A deeper question is how the populace has become so conditioned to accept a candidate who regularly lies to them. Instead of uttering difficult truths and dealing with problems in a rational and pragmatic manner (i.e., actual leadership) we are regularly electing people who simply tell us something we want to hear. Today’s world has real, difficult and painful problems to solve, and irrational solutions will only make them worse. With our political discourse so completely broken, none of the problems will be addressed much less solved. Our nation will literally drown in the bullshit we are being fed.

It is the general victory of showmanship and entertainment. The superficial and bombastic rule the day. I think that Trump is committing one of the greatest frauds of all time. He is completely and utterly unfit for office, yet has a reasonable (or perhaps unreasonable) chance to win the election. The fraud is being committed in plain sight and the fact that he speaks falsehoods at a marvelously high rate without any of the normative ill effects. Trump’s victory is testimony to how gullible the public is to complete bullshit. This gullibility reflects the lack of will on the part of the public to address real issues. With the sort of “leadership” that Trump represents, the ability to address real problems will further erode. The big irony is that Trump’s mantra of “Make America Great Again” is the direct opposite impact of his message. Trump’s sort of leadership destroys the capacity of the Nation to solve the sort of problems that lead to actual greatness. He is hastening the decline of the United States by choking our will to act in a tidal wave of bullshit.

There is a lot more bullshit in society than just Trump; he is just the most obvious example right now. Those who master bullshit win the day today, and it drives the depth of the WTF moments. Fundamentally there are forces in society today that are driving us toward the sorts of outcomes that cause us to think, “WTF?” For example we are prioritizing a high degree of micromanagement over achievement due to the risks associated with giving people freedom. Freedom encourages achievement, but also carries the risk of scandal when people abuse their freedom. Without the risks you cannot have the achievements. Today the priority is no scandal and accomplishment simply isn’t important enough to empower anyone. We are developing systems of management that serve to disempower people so that they don’t do anything unpredictable (like achieve something!).

The effect of all of this is an increasing disconnect from achievement and the concept of accountability. The end point is that the transition of achievement into bullshit is driven by the needs to market results, and marketed results being impossible to distinguish from actual results by most people. This is the sort of path that leads to our broken political discourse. When bullshit becomes identical to facts, the value and power of facts are absolutely destroyed. We are left with a situation where falsehoods are viewed as having equal footing with truth. Things like science, and the general concept of leadership by the elites in society becomes something to be reviled. We get Donald Trump as a viable candidate for President.

I wonder deeply about the extent to which things like the Internet play into this dynamic. Does the Internet allow bullshit to be presented with equality to bona fide facts? Does the Internet and computers allow a degree of micromanagement that strangles achievement? Does the Internet produce new patterns in society that we don’t understand much less have the capacity to manage? What is the value of information if it can’t be managed or understood in any way that is beyond superficial? The real danger is that people will gravitate toward what they want to view as facts instead of confronting issues that are unpleasant. The danger seems to be playing out in the political events in the United States and beyond.

Like any technology the Internet is not either good or bad by definition. It is a tool that may be used for either the benefit or the detriment of society. One way to look at the Internet is as an accelerator for what would happen societally. Information and change is happening faster and it is lubricating changes to take effect at a high pace. On the one hand we have an incredible ability to communicate with people that is beyond the capacity to even imagine a generation ago. The same communication mechanisms produces a deluge of information we are drowning and input to a degree that is choking people’s capacity to process what they are being fed. What good is the information, if the people receiving it are unable to comprehend it sufficiently to take action? or if people are unable to distinguish the proper actionable information from the complete garbage?

A force that adds to entire mix is a system that increasingly only values the capacity to monetize things. This has destroyed the ability of the media to act as a referee in society. Facts and lies are now a free for all. Scandal and fiction sell far better than facts and truth. As a result we scandalize everything. As a result small probability events are drummed up to drive better ratings (the monetization of the news), and scare the public. The scared public then acts to try to control these false risks and fears through accountability, and the downward spiral of bullshit begins. Society today is driven by fear and the desire to avoid being afraid. Risk is avoided and failure is punished. Today failure is a scandal and our ability to accomplish anything of substance is sacrificed to avoid the potential of scandal.

All of these forces are increasingly driving the elites in society (and increasingly the elites are simply those who have a modicum of education) to look at events and say “WTF?” I mean what the actual fuck is going on? The movie Idiocracy was set 500 years in the future, and yet we seem to be moving toward that vision of the future at an accelerated path that makes anyone educated enough to see what is happening tremble with fear. The sort of complete societal shitshow in the movie seems to be unfolding in front of our very eyes today. The mind-numbing effects of reality show television and pervasive low-brow entertainment is spreading like a plague. Donald Trump is the most obvious evidence of how bad things have gotten.

The sort of terrible outcomes we see obviously through our broken political discourse are happening across society. The scientific world I work in is no different. The low-brow and superficial are dominating the dialog. Our programs are dominated by strangling micromanagement that operates in the name of accountability, but really speaks volumes about the lack of trust. Furthermore the low-brow dialog simply reflects the societal desire to eliminate the technical elites from the process. This also connects back to the micromanagement because the elites can’t be trusted either. It’s become better to speak to the uneducated common man who you can “have a beer with” than trust the gibberish coming from an elite. As a result the rise of complete bullshit as technical achievements has occurred. When the people in charge can’t distinguish between Nobel Prize winning work and complete pseudo-science, the low-bar wins out. Those of us who know better are left with nothing to do but say What the Fuck? Over and over again.

The bottom line is that the Donald Trump phenomenon isn’t a localized event; it is the result of a deeply broken society. These type of WTF events are all around us every day albeit in lesser forms. Our workplaces are teaming with WFT moments. We take WTF training for WTF problems. We have WTF micromanagement that serves no purpose except to provide people with a false sense of security that nothing scandalous is going on. The WTF moment is that the micromanagement is scandalous in and of itself. All the while our economic health stands at the abyss of calamity because most business systems are devised to be wealth-transfer mechanisms rather than value creation or customer satisfaction mechanisms.

We live in a world where complete stupidity such as anti-vaxxers, climate change denial, creationists,… all seem to be taken as seriously as the science stacked against them. WTF? When real scientists are ignored in comparison to celebrities and politicians as the oracles of truth, we are lost. We waste immense amounts of time, energy, money and karma preventing things that will never happen, yet doing these things is a priority. WTF? What the fuck! Indeed! All of this is corrosive in the extreme to the very fabric of our society. The corrosion is visible in the most repugnant canary every seen in our collective coalmine, the Donald. He is a magnificent WTF indictment of our entire society.

People don’t want to buy a quarter-inch drill. They want a quarter-inch hole.

― Clayton M. Christensen

The truth in this quote is for those looking to aspire to the greater things that a drill can help build. At the same time we all know people who love their tools and aspire to the greatest toolset money can buy, yet never build anything great. They have the world’s most awesome set of tools in their garage or work room, yet do nothing but tinker. People who build great things have a similar set of great tools, but focus on what they are building. The whole area of computing is risking becoming the hobby enthusiast who loves to show you their awesome tool box, but never have the intent of doing more than showing it off while building nothing in the process. Our supercomputers are the new prize for such enthusiasts. The core of the problem is the lack of anything important to apply these powerful tools to accomplish.

High Performance computing has become the central focus for scientific computing. It is just a tool. This is a very bad thing and extremely unhealthy for the future of scientific computing. The problems with making it the focal point for progress are manifestly obvious if one thinks about what it takes to make scientific computing work. The root of the problem is the lack of thought going into our current programs, and ultimately a failure to understand that HPC isn’t what we should be focused on; it is a necessary part of how scientific computing is delivered. The important part of what we do is modeling and simulation, which can transform how we do science and engineering. HPC can’t transform anything except electricity into heat, and relies upon modeling and simulation for its value. While HPC is important and essential to the whole enterprise the other aspects of proper delivery of scientific computing are so starved for attention that they may simply fail to exist soon.

For all the talk of creating a healthy ecosystem for HPC the programs comprised today are woefully inadequate towards achieving that end. The computer hardware focus exists because it is tangible and one can point at a big mainframe and say “I bought that!” It misses the key aspects of the field necessary for success, and even worse the key value in scientific computing. Scientific computing is a set of tools that allow the efficient manipulation of models of reality to allow exploration, design and understanding of the World without actually having to experiment with the real thing. Everything valuable about computing is in reality and what I will explain below is that the computer hardware is the most distant and least important aspect of the ecosystem that makes scientific computing important, useful and valuable to society.

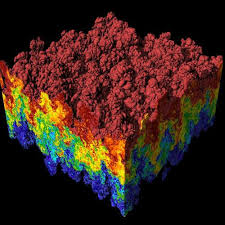Effectively we are creating an ecosystem where the apex predators are missing, and this isn’t a good thing. The models we use in science are the key to everything. They are the translation of our understanding into mathematics that we can solve and manipulate to explore our collective reality. Computers allow us to solve much more elaborate models than otherwise possible, but little else. The core of the value in scientific computing are the capacity of the models to explain and examine the physical World we live in. They are the “apex predators” in the scientific computing system, and taking this analogy further our models are becoming virtual dinosaurs where evolution has ceased to take place. The models in our codes are becoming a set of fossilized skeletons and not at all alive, evolving and growing.

The process of our models becoming fossilized is a form of living death. Models need to evolve, change, grow or even become extinct for science to be healthy. In the parlance of computing, models are embedded in codes and form the basis of a code’s connection to reality. When a code becomes a legacy code, the model(s) in the code become legacy as well. A healthy ecosystem would allow for the models (codes) to confront reality and come away changed in substantive ways including evolving, adapting and even dying as a result. In many cases the current state of scientific computing with its focus on HPC does not serve this purpose. The forces that change codes are diverse and broad. Being able to run codes at scales never before seen should produce outcomes that sometimes lead to a code’s (model’s) demise. The demise or failure of models is an important and health part of an ecosystems missing today.

People do not seem to understand that faulty models render the entirety of the computing exercise moot. Yes, the computational results may be rendered into exciting and eye-catching pictures suitable for entertaining and enchanting various non-experts including congressmen, generals, business leaders and the general public. These eye-catching pictures are getting better all the time and now form the basis of a lot of the special effects in the movies. All of this does nothing for how well the models capture reality. The deepest truth is that no amount of computer power, numerical accuracy, mesh refinement, or computational speed can rescue a model that is incorrect. The entire process of validation against observations made in reality must be applied to determine if models are correct. HPC does little to solve this problem. If the validation provides evidence that the model is wrong and a more complex model is needed then HPC can provide a tool to solve it.

The modern computing environment whether seen in a cell phone, or a supercomputer is a marvel of the modern World. It requires a host of technologies working togetherseamlessly to produce incredible things. We have immensely complex machines that produce important outcomes in the real world through a set of interweaved systems that translate electrical signals into instructions understood by the computer and humans, into discrete equations, solved by mathematical procedures that describe the real world and ultimately compared with measured quantities in systems we care about. If we look at our focus today, the complexity of focus is the part of the technology that connects very elaborate complex computers to the instructions understood both by computers and people. This is electrical engineering and computer science. The focus begins to dampen in the part of the system where the mathematics, physics and reality comes in. These activities form the bond between the computer and reality. These activities are not a priority, and conspicuously diminished significantly by today’s HPC.

HPC today is structured in a manner to eviscerate fields that have been essential to the success of scientific computing. A good example is our applied mathematics programs. In many cases applied mathematics has become little more than scientific programming and code development. Far too little actual mathematics is happening today, and far too much focus is seen in productizing mathematics in software. Many people with training in applied mathematics only do software development today and spend little or no effort in doing analysis and development away from their keyboards. It isn’t that software development isn’t important, the issue is the lack of balance in the overall ratio of mathematics to software. The power and beauty of applied mathematics must be harnessed to achieve success in modeling and simulation. Today we are simply bypassing this essential part of the problem to focus on delivering software products.

Similar issues are present with applied physics work. A healthy research environment for making progress in HPC would see far greater changes in modeling. A key aspect of modeling is the presence of experiments that challenge the ability of modeling to produce good useful representations of reality. Today such experimental evidence is sorely lacking and significantly hampered by the inability to take risks and push the envelope with real things. If we push the envelope on things in the real world it will expose our understanding to deep scrutiny. Such scrutiny will necessitate changes to our modeling. Without this virtuous cycle the drive to improve is utterly lacking.

Another missing element in the overall mix is the extent to which modeling and simulation supports activities pushing society forward. We seem to be in an era where society is not interested in progressing at anything these days. Instead we are trying to work toward a risk free world where everyone is completely safe and entirely divorced from ever failing at anything. Because of this environment the overall push for better technology is blunted to the degree that nothing of substance ever gets done. The maxim of modern life is that vast amounts of effort will be expended to assure that trivially possible things are assured of not happening. No small possibility of a dire outcome is too small to inhibit the expenditure of vast resources to make this smaller. This explains so much of what is wrong with the World today. We will bankrupt ourselves to achieve many expensive and unimportant outcomes that are completely unnecessary. Taking this view of the World allows us to explain to utter stupidity of the HPC world.

The origin, birth and impact of modeling and simulation arises from its support of activities essential to making societal progress. Without activities working toward societal progress (or at least the scientific-technological aspects of this) modeling and simulation is stranded in stasis. Progress in modeling and simulation is utterly tied to work in areas where big things are happening. High performance computing arose to prominence as a tool to allow modeling and simulation to tackle problems of greater complexity and difficulty. That said HPC is only one of the tools allowing this to happen. There is a complex and vast chain of tools necessary for modeling and simulation to succeed. It is arguable that HPC isn’t even the most important or lynchpin tool in the mix. If one looks at the chain of things that needs to work together the actual computer is the farthest removed from the reality we are aiming to master? If anything along the chain of tools closer to reality breaks, the computer is rendered useless. In other words, the computer can work perfectly and be infinitely fast and efficient, yet still be useless unless the software running on it is correct. Furthermore in the exercise of modeling and simulation, the software must be based on firm mathematical and physical principles, or it will be similarly useless. This last key step is exactly the part of the overall approach we are putting little or no effort in to in our current approach. Despite this lack of evidence we have made HPC central to success today. Too much focus on a tool of limited importance will swallow resources that could have been expended on more impactful activities. Ultimately the drivers for progress at a societal level are necessary for any of this work to have actual meaning.

If I’m being honest modeling and simulation is just a tool as well. As a tool it is much closer to the building of something great than the computers are. Used properly it can have a much greater impact on the capacity for helping produce great things than the computers can. What we miss more than anything is the focus on achieving great things as a society. We are too busy trying to save ourselves from a myriad of minute and vanishing threats to our safety. As long as we are so unremittingly risk adverse we will accomplish nothing. Our focus on big computers over big achievements is just a small reflection of this vast societal ill.

To the man who only has a hammer, everything he encounters begins to look like a nail.

― Abraham H. Maslow

Good judgment comes from experience, and experience – well, that comes from poor judgment.

― A.A. Milne

To avoid the sort of implicit assumption of ZERO uncertainty one can use (expert) judgment to fill in the information gap. This can be accomplished in a distinctly principled fashion and always works better with a basis in evidence. The key is the recognition that we base our uncertainty on a model (a model that is associated with error too). The models are fairly standard and need a certain minimum amount of information to be solvable, and we are always better off with too much information making it effectively over-determined. Here we look at several forms of models that lead to uncertainty estimation including discretization error, and statistical models applicable to epistemic or experimental uncertainty.

Maturity, one discovers, has everything to do with the acceptance of ‘not knowing.

― Mark Z. Danielewski

For discretization error the model is quite simple where is the mesh converged solution, is the solution on the mesh and is the mesh length scale, is the (observed) rate of convergence, and is a proportionality constant. We have three unknowns so we need at leastmeshes to solve the error model exactly or more if we solve it in some sort of optimal manner. We recently had a method published that discusses how to include expert judgment in the determination of numerical error and uncertainty using models of this type. This model can be solved along with data using minimization techniques including the expert judgment as constraints on the solution for the unknowns. For both the over- or the under-determined cases different minimizations one can get multiple solutions to the model and robust statistical techniques may be used to find the “best” answers. This means that one needs to resort to more than simple curve fitting, and least squares procedures; one needs to solve a nonlinear problem associated with minimizing the fitting error (i.e., residuals) with respect to other error representations.

For extreme under-determined cases unknown variables can be completely eliminated by simply choosing the solution based on expert judgment. For numerical error an obvious example is assuming that calculations are converging at an expert-defined rate. Of course the rate assumed needs an adequate justification based on a combination of information associated with the nature of the numerical method and the solution to the problem. A key assumption that often does not hold up is the achievement of the method’s theoretical rate of convergence for realistic problems. In many cases a high-order method will perform at a lower rate of convergence because the problem has a structure with less regularity than necessary for the high-order accuracy. Problems with shocks or other forms of discontinuities will not usually support high-order results and a good operating assumption is a first-order convergence rate.

To make things concrete let’s tackle a couple of examples of how all of this might work. In the paper published recently we looked at solution verification when people use two meshes instead of the three needed to fully determine the error model. This seems kind of extreme, but in this post the example is the cases where people only use a single mesh. Seemingly we can do nothing at all to estimate uncertainty, but as I explained last week, this is the time to bear down and include an uncertainty because it is the most uncertain situation, and the most important time to assess it. Instead people throw up their hands and do nothing at all, which is the worst thing to do. So we have a single solution at and need to add information to allow the solution of our error model, . The simplest way to get to an solvable error model is to simply propose a value for the mesh converged solution, , which then can be used to provide an uncertainty estimate,    |A – multiplied by an appropriate safety factor .

This is a rather strong assumption to make. We might be better served by providing a range values for either the convergence rate of the solution itself. In this way we provide a bit more deference in what we are suggesting as the level of uncertainty, which is definitely called for in this case since we are so information poor. Again the use of an appropriate safety factor is called for, on the order of 2 to 3 in value. From statistical arguments the safety factor of 2 has some merit while 3 is associated with solution verification practice proposed by Roache. All of this is strongly associated with the need to make an estimate in a case where too little work has been done to make a direct estimate. If we are adding information that is weakly related to the actual problem we are solving, the safety factor is essential to account for the lack of knowledge. Furthermore we want to enable the circumstance where more work in active problem solving will allow the uncertainties to be reduced!

A lot of this information is probably good to include as part of the analysis when you have enough information too. The right way to think about this information is as constraints on the solution. If the constraints are active they have been triggered by the analysis and help determine the solution. If the constraints have no effect on the solution then they are proven to be correct given the data. In this way the solution can be shown to be consistent with the views of the expertise. If one is in the circumstance where the expert judgment is completely determining the solution, one should be very wary as this is a big red flag.

Other numerical effects need models for their error and uncertainty too. Linear and nonlinear error plus round-off error all can contribute to the overall uncertainty. A starting point would be the same model as the discretization error, but using the tolerances from the linear or nonlinear solution as . The starting assumption is often that these are dominated by discretization error, or tied to the discretization. Evidence in support of these assumptions is generally weak to nonexistent. For round-off errors the modeling is similar, but all of these errors can be magnified in the face of instability. A key is to provide some sort of assessment of their aggregate impact on the results and not explicitly ignore them.

Other parts of the uncertainty estimation are much more amenable to statistical structures for uncertainty. This includes the type of uncertainty that too often provides (wrongly!) the entirety of uncertainty estimation, parametric uncertainty. This problem is a direct result of the availability of tools that allow the estimation of parametric uncertainty magnitude. In addition to parametric uncertainty, random aleatory uncertainties, experimental uncertainty and deep model form uncertainty all may be examined using statistical approaches. In many ways the situation is far better than for discretization error, but in other ways the situation more dire. Things are better because statistical models can be evaluated using less data, and errors can be estimated using standard approaches. The situation is dire because often the issues being radically under-sampled are reality, not the model of reality simulations are based on.

Uncertainty is a quality to be cherished, therefore – if not for it, who would dare to undertake anything?

― Villiers de L’Isle-Adam

In the same way as numerical uncertainty, the first thing to decide upon is the model. A standard modeling assumption is the use of the normal or Gaussian distribution as the starting assumption. This is almost always chosen as a default. A reasonable blog post title would be “The default probability distribution is always Gaussian”. A good thing for a distribution is that we can start to assess it beginning with two data points. A bad and common situation is that we only have a single data point. Thus uncertainty estimation is impossible without adding information from somewhere, and an expert judgment is the obvious place to look. With statistical data and its quality we can apply the standard error estimation using the sample size to scale the additional uncertainty driven by poor sampling, 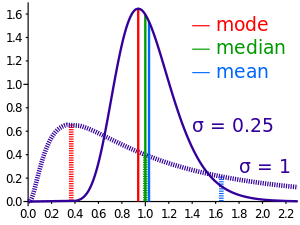where is the number of samples.

There are some simple ideas to apply in the case of the assumed Gaussian and a single data point. A couple of reasonable pieces of information can be added, one being an expert judged standard deviation and then by fiat making the single data point the mean of the distribution. A second assumption could be used where the mean of the distribution is defined by expert judgment, which then defines the standard deviation,  |A – where is the defined mean, and is the data point. In these cases the standard error estimate would be equal to where . Both of these approaches have the strengths and weaknesses, and include the strong assumption of the normal distribution.

In a lot of cases a better simple assumption about the statistical distribution would be to use a uniform distribution. The issue with the uniform distribution would be identifying the width of the distribution. To define the basic distribution you need at least two pieces of information just as the normal (Gaussian) distribution. The subtleties are different and need some discussion. The width of a uniform distribution is defined by – . A question is how representative a single piece of information would actually be? Does one center the distribution about ? One could be left with needing to add two pieces of information instead of one by defining and . This then allows a fairly straightforward assessment of the uncertainty.

For statistical models eventually one might resort to using a Bayesian method to encode the expert judgment in defining a prior distribution. In general terms this might seem to be an absolutely key approach to structure the expert judgment where statistical modeling is called for. The basic form of Bayes theorem is where is the probability of given , is the probability of and so on. A great deal of the power of the method depends on having a good (or expert) handle on all the terms on the right hand side of the equation. Bayes theorem would seem to be an ideal framework for the application of expert judgment through the decision about the nature of the prior.

The mistake is thinking that there can be an antidote to the uncertainty.

― David Levithan

A key to this entire discussion is the need to resist the default uncertainty of ZERO as a principle. It would be best if real problem specific work were conducted to estimate uncertainties, the right calculations, right meshes and right experiments. If one doesn’t have the time, money or willingness, the answer is to call upon experts to fill in the gap using justifiable assumptions and information while taking an appropriate penalty for the lack of effort. This would go a long way to improving the state of practice in computational science, modeling and simulation.

Children must be taught how to think, not what to think.

― Margaret Mead

Rider, William, Walt Witkowski, James R. Kamm, and Tim Wildey. “Robust verification analysis.” Journal of Computational Physics 307 (2016): 146-163.

As long as you’re moving, it’s easier to steer.

― Anonymous

Just to be clear, this isn’t a good thing; it is a very bad thing!

I have noticed that we tend to accept a phenomenally common and undeniably unfortunate practice where a failure to assess uncertainty means that the uncertainty reported (acknowledged, accepted) is identically ZERO. In other words if we do nothing at all, no work, no judgment, the work (modeling, simulation, experiment, test) is allowed to provide an uncertainty that is ZERO. This encourages scientists and engineers to continue to do nothing because this wildly optimistic assessment is a seeming benefit. If somebody does work to estimate the uncertainty the degree of uncertainty always gets larger as a result. This practice is desperately harmful to the practice and progress in science and incredibly common.

Of course this isn’t the reality, the uncertainty is actually some value, but the lack of assessed uncertainty is allowed to be accepted as ZERO. The problem is the failure of other scientists and engineers to demand an assessment instead of simply accepting the lack of due diligence or outright curiosity and common sense. The reality is that the situation where the lack of knowledge is so dramatic, the estimated uncertainty should actually be much larger to account for this lack of knowledge. Instead we create a cynical cycle where more information is greeted by more uncertainty rather than less. The only way to create a virtuous cycle is the acknowledgement that little information should mean large uncertainties, and part of the reward for good work is greater certainty (and lower uncertainty).

This entire post is related to a rather simple observation that has broad applications for how science and engineering is practiced today. A great deal of work has this zero uncertainty writ large, i.e., there is no reported uncertainty at all, none, ZERO. Yet, despite of the demonstrable and manifest shortcomings, a gullible or lazy community readily accepts the incomplete work. Some of the better work has uncertainties associated with it, but almost always varying degrees of incompleteness. Of course one should acknowledge up front that uncertainty estimation is always incomplete, but the degree of incompleteness can be spellbindingly large.

One way to deal with all of this uncertainty is to introduce a taxonomy of uncertainty where we can start to organize our lack of knowledge. For modeling and simulation exercises I’m suggesting that three big bins for uncertainty be used: numerical, epistemic modeling, and modeling discrepancy. Each of these categories has additional subcategories that may be used to organize the work toward a better and more complete technical assessment. In the definition for each category we get the idea of the texture in each, and an explicit view of intrinsic incompleteness.

• Numerical: Discretization (time, space, distribution), nonlinear approximation, linear convergence, mesh, geometry, parallel computation, roundoff,…
• Epistemic Modeling: black box parametric, Bayesian, white box testing, evidence theory, polynomial chaos, boundary conditions, initial conditions, statistical,…
• Modeling discrepancy: Data uncertainty, model form, mean uncertainty, systematic bias, boundary conditions, initial conditions, measurement, statistical, …

A very specific thing to note is that the ability to assess any of these uncertainties is always incomplete and inadequate. Admitting and providing some deference to this nature is extremely important in getting to a better state of affairs. A general principle to strive for in uncertainty estimation is a state where the application of greater effort yields smaller uncertainties. A way to achieve this nature of things is to penalize the uncertainty estimation to account for incomplete information. Statistical methods always account for sampling by increasing a standard error proportionally to the root of the number of samples. As such there is an explicit benefit for gathering more data to reduce the uncertainty. This sort of measure is well suited to encourage a virtuous cycle of information collection. Instead modeling and simulation accepts a poisonous cycle where more information implicitly penalizes the effort by increasing uncertainty.

This whole post is predicated on the observation that we willingly enter into a system where effort increases the uncertainty. The direct opposite should be the objective where more effort results in smaller uncertainty. We also need to embrace a state where we recognize that the universe has an irreducible core of uncertainty. Admitting that perfect knowledge and prediction is impossible will allow us to focus more acutely on what we can predict. This is really a situation where we are willfully ignorant and over-confident about your knowledge. One might tag some of the general issue with reproducibility and replicatability of science to the same phenomena. Any effort that reports to provide a perfect set of data perfectly predicting reality should be rejected as being utterly ridiculous.

One of the next things to bring to the table is the application of expert knowledge and judgment to fill in where stronger technical work is missing. Today expert judgment is implicitly present in the lack of assessment. It is a dangerous situation where experts simply assert that things are true or certain. Instead of this expert system being directly identified, it is embedded in the results. A much better state of affairs is to ask for the uncertainty and the evidence for its value. If there has been work to assess the uncertainty this can be provided. If instead, the uncertainty is based on some sort expert judgment or previous experience, the evidence can be provided in this form.

Now let us be more concrete in the example of what this sort of evidence might look like within the expressed taxonomy for uncertainty. I’ll start with numerical uncertainty estimation that is the most commonly completely non-assessed uncertainty. Far too often a single calculation is simply shown and used without any discussion. In slightly better cases, the calculation will be given with some comments on the sensitivity of the results to the mesh and the statement that numerical errors are negligible at the mesh given. Don’t buy it! This is usually complete bullshit! In every case where no quantitative uncertainty is explicitly provided, you should be suspicious. In other cases unless the reasoning is stated as being expertise or experience it should be questioned. If it is stated as being experiential then the basis for this experience and its documentation should be given explicitly along with evidence that it is directly relevant.

So what does a better assessment look like?

Under ideal circumstances you would use a model for the error (uncertainty) and do enough computational work to determine the model. The model or models would characterize all of the numerical effects influencing results. Most commonly, the discretization error is assumed to be the dominant numerical uncertainty (again evidence should be given). If the error can be defined as being dependent on a single spatial length scale, the standard error model can be used and requires three meshes be used to determine its coefficients. This best practice is remarkably uncommon in practice. If fewer meshes are used, the model is under-determined and information in terms of expert judgment should be added. I have worked on the case of only two meshes being used, but it is clear what to do in that case.

In many cases there is no second mesh to provide any basis for standard numerical error estimation. Far too many calculational efforts provide a single calculation without any idea of the requisite uncertainties. In a nutshell, the philosophy in many cases is that the goal is to complete the best single calculation possible and creating a calculation that is capable of being assessed is not a priority. In other words the value proposition for computation is either do the best single calculation without any idea of the uncertainty versus a lower quality simulation with a well-defined assessment of uncertainty. Today the best single calculation is the default approach. This best single calculation then uses the default uncertainty estimate of exactly ZERO because nothing else is done. We need to adopt an attitude that will reject this approach because of the dangers associated with accepting a calculation without any quality assessment.

In the absence of data and direct work to support a strong technical assessment of uncertainty we have no choice except to provide evidence via expert judgment and experience. A significant advance would be a general sense that such assessments be expected and the default ZERO uncertainty is never accepted. For example there are situations where single experiments are conducted without any knowledge of how the results of the experiment fit within any distribution of results. The standard approach to modeling is a desire to exactly replicate the results as if the experiment were a well-posed initial value problem instead of one realization of a distribution of results. We end up chasing our tails in the process and inhibiting progress. Again we are left in the same boat, as before, the default uncertainty in the experimental data is ZERO. Instead we have no serious attempt to examine the width and nature of the distribution in our assessments. The result is a lack of focus on the true nature of our problems and inhibitions on progress.

The problems just continue in the assessment of various uncertainty sources. In many cases the practice of uncertainty estimation is viewed only as the establishment of the degree of uncertainty is modeling parameters used in various closure models. This is often termed as epistemic uncertainty or lack of knowledge. This sometimes provides the only identified uncertainty in a calculation because tools exist for creating this data from calculations (often using a Monte Carlo sampling approach). In other words the parametric uncertainty is often presented as being all the uncertainty! Such studies are rarely complete and always fail to include the full spectrum of parameters in modeling. Such studies are intrinsically limited by being embedded in a code that has other unchallenged assumptions.

This is a virtue, but ignores broader modeling issues almost completely. For example the basic equations and model used in simulations is rarely, if ever questioned. The governing equations minus the closure are assumed to be correct a priori. This is an extremely dangerous situation because these equations are not handed down from the creator on stone tablets, but full of assumptions that should be challenged and validated with regularity. Instead this happens with such complete rarity despite being the dominant source of error in cases. When this is true the capacity to create a predictive simulation is completely impossible. Take the application of incompressible flow equations, which is rarely questioned. These equations have a number of stark approximations that are taken as the truth almost without thought. The various unphysical aspects of the approximation are ignored. For compressible flow the equations are based on equilibrium assumptions, which are rarely challenged or studied.

A second area of systematic and egregious oversight by the community is aleatory or random uncertainty. This sort of uncertainty is clearly overlooked by our modeling approach in a way that most people fail to appreciate. Our models and governing equations are oriented toward solving the average or mean solution for a given engineering or science problem. This key question is usually muddled together in modeling by adopting an approach that mixes a specific experimental event with a model focused on the average. This results in a model that has an unclear separation of the general and specific. Few experiments or events being simulated are viewed from the context that they are simply a single instantiation of a distribution of possible outcomes. The distribution of possible outcomes is generally completely unknown and not even considered. This leads to an important source of systematic uncertainty that is completely ignored.

It doesn’t matter how beautiful your theory is … If it doesn’t agree with experiment, it’s wrong.

― Richard Feynman

Almost every validation exercise tries to examine the experiment as a well-posed initial value problem with a single correct answer instead of a single possible realization from an unknown distribution. More and more the nature of the distribution is the core of the scientific or engineering question we want to answer, yet our modeling approach is hopelessly stuck in the past because we are not framing the question we are answering thoughtfully. Often the key question we need to answer is how likely a certain bad outcome will be. We want to know the likelihood of extreme events given a set of changes in a system. Think about things like what does a hundred year flood look like under a scenario of climate change, or the likelihood that a mechanical part might fail under normal usage. Instead our fundamental models being the average response for the system are left to infer these extreme events from the average often without any knowledge of the underlying distributions. This implies a need to change the fundamental approach we take to modeling, but we won’t until we start to ask the right questions and characterize the right uncertainties.

One should avoid carrying out an experiment requiring more than 10 per cent accuracy.

― Walther Nernst

The key to progress is work toward some best practices that avoid these pitfalls. First and foremost a modeling and simulation activity should never allow itself to report or even imply that key uncertainties be ZERO. If one has lots of data and make efforts to assess then uncertainties can be assigned through strong technical arguments. This is terribly or even embarrassingly uncommon even today. If one does not have the data or calculations to support uncertainty estimation then significant amounts of expert judgment and strong assumptions are necessary to estimate uncertainties. The key is to make a significant commitment to being honest about what isn’t known and take a penalty for lack of knowledge and understanding. That penalty should be well grounded in evidence and experience. Making progress in these areas is essential to make modeling and simulation a vehicle appropriate to the hype we hear all the time.

Stagnation is self-abdication.

― Ryan Talbot

Modeling and simulation is looked at as one of the great opportunities for industrial, scientific and engineering improvements for society. Right now we are hinging our improvements on a mass of software being moved onto increasingly exotic (and powerful) computers. Increasingly the whole of our effort in modeling and simulation is being reduced to nothing but a software development activity. The holistic and integrating nature of modeling and simulation is being hollowed out and lost to a series of fatal assumptions. One of the places where computing’s power cannot change is how we practice our computational efforts. It can enable the practices in modeling and simulation by making it possible to do more computation. The key to fixing this dynamic is a commitment to understanding the nature and limits of our capability. Today we just assume that our modeling and simulation has mastery and no such assessment is needed.

The computational capability does nothing to improve experimental sciences necessary value in challenging our theory. Moreover the whole sequence of necessary activities like model development, and analysis, method and algorithm development along with experimental science and engineering are all receiving almost no attention today. These activities are absolutely necessary for modeling and simulation success along with the sort of systematic practices I’ve elaborated on in this post. Without a sea change in the attitude toward how modeling and simulation is practiced and what it depends upon, its promise as a technology will be stillborn and nullified by our collective hubris.

It is high time for those working to progress modeling and simulation to focus energy and effort it is needed. Today we are avoiding a rational discussion of how to make modeling and simulation successful, and relying on hype to govern our decisions. The goal should not be to assure that high performance computing is healthy, but rather modeling and simulation (or big data analysis) is healthy. High performance computing is simply a necessary tool for these capabilities, but not the soul of either. We need to make sure the soul of modeling and simulation is healthy rather than the corrupted mass of stagnation we have.

You view the world from within a model.

― Nassim Nicholas Taleb

…beauty is not symmetry of parts- that’s so impotent -as Mishima says, beauty is something that attacks, overpowers, robs, & finally destroys…

― John Geddes

In much of physics a great deal is made of the power of symmetry. The belief is that symmetry is a powerful tool, but also a compelling source of beauty and depth. In fluid mechanics the really cool stuff happens when the symmetry is broken. The power and depth of consequence comes from the asymmetric part of the solution. When things are symmetric they tend to be boring and uninteresting, and nothing beautiful or complex arises. I’ll be so bold as to say that the power of this essential asymmetry hasn’t been fully exploited, but could be even more magnificent.

Fluid mechanics at its simplest is something called Stokes flow, basically motion so slow that it is solely governed by viscous forces. This is the asymptotic state where the Reynolds number (the ratio of inertial to viscous forces) is identically zero. It’s a bit oxymoronic as it is never reached, it’s the equations of motion without any motion or where the motion can be ignored. In this limit flows preserve their basic symmetries to a very high degree.

Basically nothing interesting happens and the whole thing is basically a giant boring glop of nothing. It is nice because lots of pretty math can be done in this limit. The equations are very well behaved and solutions have tremendous regularity and simplicity. Let the fluid move and take the Reynolds number away from zero and cool things almost immediately happen. The big thing is the symmetry is broken and the flow begins to contort, and wind into amazing shapes. Continue to raise the Reynolds number and the asymmetries pile up and we have turbulence, chaos and our understanding goes out the window. At the same time the whole thing produces patterns and structures of immense and inspiring beauty. With symmetry fluid mechanics is dull as dirt; without symmetry it is amazing and something to marveled at.

So, let’s dig a bit deeper into the nature of these asymmetries and the opportunity to take them even further.

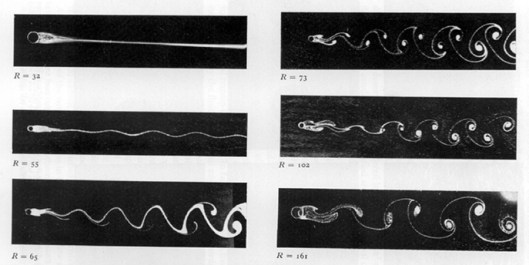The fundamental asymmetry in physics is the arrow of time, and its close association with entropy. The connection with asymmetry and entropy is quite clear and strong for shock waves where the mathematical theory is well-developed and accepted. The simplest case to examine is Burgers’ equation, , or its conservation form . This equation supports shocks and rarefactions, and their formation is determined by the sign of . If one takes the gradient of the governing equation in space, you can see the solution forms a Ricatti equation along characteristics, . The solution on characteristics tells one the fate of the solution, . The thing to recognize that the denominator will go to zero if and the value of the derivative will become unbounded, i.e., form a shock.

The process in fluid dynamics is similar. If the viscosity is sufficiently small and the gradients of velocity are negative, a shock will form. It is inevitable as death and taxes. Moving back to Burgers’ equation briefly we can also see another aspect of the dynamics that isn’t so commonly known, the presence of dissipation in the absence of viscosity. Without viscosity for the rarefied flow where gradients diminish there is no dissipation. For a shock there is dissipation, and the form of it will be quite familiar by the end of the post. If one forms an equation for the evolution of the energy in a Burgers’ flow and looks at the solution for a shock via the jump conditions a discrepancy is uncovered, the rate of kinetic energy dissipation is . The same basic character is shared by shock waves and incompressible turbulent flows. It implies the presence of a discontinuity in the model of the flow.

On the one hand the form seems to be unavoidable dimensionally, on the other it is a profound result that provides the basis of the Clay prize for turbulence. It gets to the core of my belief that to a very large degree the understanding of turbulence will elude us as long as we use the intrinsically unphysical incompressible approximation. This may seem controversial, but incompressibility is an approximation to reality, not a fundamental relation. As such its utility is dependent upon the application. It is undeniably useful, but has limits, which are shamelessly exposed by turbulence. Without viscosity the equations governing incompressible flows are pathological in the extreme. Deep mathematical analysis has been unable to find singular solutions of the nature needed to explain turbulence in incompressible flows.

The real key to understanding the issues goes to a fundamental misunderstanding about shock waves and compressibility. First, it would be very good to elaborate how the same dynamic manifests itself for the compressible Euler equations. For intents and purposes the way to look at shock formation in the Euler equations acts just like Burgers’ equation for the nonlinear characteristics. In its simplest form the Euler equations have three fundamental characteristic modes, two being nonlinear associated with acoustic (sound) waves, one being linear and associated with material motion. The nonlinear acoustic modes act just like Burgers’ equation, and propagate at a velocity of where is the fluid velocity, and is the speed of sound.

Once the Euler equations are decomposed into the characteristics and the flow is smooth everything follows as Burgers’ equation. Along the appropriate characteristic, the flow will be modulated according to the nonlinearity of the equations, which is slightly different than Burgers’ in an important manner. The nonlinearity now depends on the equation of state in a key was, the curvature of an isentrope, . This quantity is dominantly and asymptotically positive (i.e., convex), but may be negative. For ideal gases . For convex equations of state shocks then always form given enough time if the velocity gradient is negative just like Burgers’ equation.

One key thing to recognize is that the formation of the shock does not depend on the underlying Mach number of the flow. A shock always forms if the velocity is negative even as the Mach number goes to zero (the incompressible limit). Almost everything else follows as with Burgers’ equation including the dissipation relation associated with a shock wave, . Once the shock forms, the dissipation rate is proportional to the cube of the jump across the shock. In addition this limit is actually most appropriate in the zero Mach number limit (i.e., the same limit as incompressible flow!).

Shocks aren’t just supersonic phenomena; they are a result of solving the equations in a limit where this viscous terms are small enough to neglect (i.e., the high Reynolds’ number limit!). So just to sum up, the shock formation along with intrinsic dissipation is most valid in the limits where we think of turbulence. We see that this key effect is a direct result of the asymmetric effect of a velocity gradient on the flow. For most flows where the equation of state is convex, the negative velocity gradient sharpens flow features into shocks that dissipate energy regardless of the value of viscosity. Positive velocity gradients smooth the flow and modify the flow via rarefying the flow. Note that physically admissible non-convex equations of state (really isolated regions in state space) have the opposite character. If one could run a classical turbulence experiment where the fluid is non-convex, the conceptual leap I am suggesting could be tested directly because the asymmetry in turbulence would be associated with positive rather than negative velocity gradients.

Now we can examine the basic known theory of turbulence that is so vexing to everyone. Kolmogorov came up with three key relations for turbulent flows. The spectral nature of turbulence is the best known where one looks at the frequency decomposition of the turbulence flow, and finds a distinct region where the decay of energy shows -5/3 slope. There is a lesser know relation of velocity correlations known as the 2/3 law. I believe the most important relation is known as the 4/5 law for the asymptotic decay of kinetic energy in a high Reynolds number turbulent flow. This equation implies that dissipation occurs in the absence of viscosity (sound familiar?).

The law is stated as . The subscript means longitudinal where the differences are taken in the direction the velocity is moving over a distance . This relation implies a distinct asymmetry in the equations that means negative gradients are intrinsically sharper than positive gradients. This is exactly what happens in compressible flows. Kolmogorov derived this relation from the incompressible flow equations and it has been strongly confirmed by observations. The whole issue associated with the (in)famous Clay prize is the explanation of this law in the mathematical admissible solutions of the incompressible equations. This law suggests that the incompressible flow equations must support singularities that are in essence like a shock. My point is that the compressible equations support exactly the phenomena we seek in the right limits for turbulence. The compressible equations have none of the pathologies of the incompressible equations and have a far greater physical basis and remove the unphysical aspects of the physical-mathematical description.

The result is a conclusion that the incompressible equations are inappropriate for understanding what is happening fundamentally in turbulence. The right way to think about it is that turbulent relations are supported by the basic physics of compressible flows in the right asymptotic limits of zero Mach number, high Reynolds number limits.

Symmetry is what we see at a glance; based on the fact that there is no reason for any difference…

― Blaise Pascal

It isn’t all over; everything has not been invented; the human adventure is just beginning.

― Gene Roddenberry

Listening to the dialog on modeling and simulation is so depressing. There seems to be an assumption implicit to every discussion that all we need to do to unleash predictivesimulation is build the next generation of computers. The proposition is so shallow on the face of it as to be utterly laughable. Except no one is laughing, the programs are predicated on it. The whole mentality is damaging because it intrinsically limits our thinking about how to balance the various elements needed for progress. We see a lack of the sort of approach that can lead to progress with experimental work starved of funding and focus without the needed mathematical modeling effort necessary for utility. Actual applied mathematics has become a veritable endangered species only seen rarely in the wild.

Often a sign of expertise is noticing what doesn’t happen.

― Malcolm Gladwell

One of the really annoying aspects of the hype around computing these days is the lack of practical and pragmatic perspective on what might constitute progress. Among the topics revolving around modeling and simulation practice is the pervasive need for singularities of various types in realistic calculations of practical significance. Much of the dialog and dynamic technically seems to completely avoid the issue and act as if it isn’t a driving concern. The reality is that singularities of various forms and functions are an ever-present aspect of realistic problems and their mediation is an absolutely essential for modeling and simulation’s impact to be fully felt. We still have serious issues because of our somewhat delusional dialog on singularities.

At a fundamental level we can state that singularities don’t exist in nature, but very small or thin structures do whose details don’t matter for large scale phenomena. Thus singularities are a mathematical feature of models for large scale behavior that ignore small scale details. As such when we talk about the behavior of singularities, we are really just looking at models, and asking whether the model’s behavior is good. The important aspect of the things we call singularities is their impact on the large scale and the capacity to do useful things without looking at the small-scale details. Much, if not all of the current drive for computational power is focused on brute force submission of the small-scale details. This approach fails to ignite the sort of deep understanding that a model, which ignoring the small scales requires. Such understanding is the real role of science, not simply overwhelming things with technology.

The role of genius is not to complicate the simple, but to simplify the complicated.

― Criss Jami

The important this to capture is the universality of the small scale’s impact on the large scale. It is closely and intimately related to ideas around the role of stochastic, random structures and models for average behavior. One of the key things to really straighten out is the nature of the question we are asking the model to answer. If the question isn’t clearly articulated, the model will provide deceptive answers that will send scientists and engineers in the wrong direction. Getting this model to question dynamic sorted out is far more important to the success of modeling and simulation than any advance in computing power. It is also completely and utterly off the radar of the modern research agenda. I worry that the present focus will produce damage to the forces of progress that may take decades to undue.

A key place where singularities regularly show up is representations of geometry. It is really useful to represent things with sharp corners and rapid transitions geometrically. Our ability to simulate anything engineered would suffer immensely is we had to compute the detailed smooth parts of geometry. In many cases the detail is then computed with a sort of subgrid model, like surface roughness to represent the impact of the true non-idealized geometry. This is a key example of the treatment of such details as being almost entirely physic’s domain specific. There is not a systematic view of this across fields. The same sort of effect shows up when we marry parts together with the same or different materials.

An expert is someone who knows some of the worst mistakes that can be made in his subject, and how to avoid them.

― Werner Heisenberg

Again the details are immense, the simplification is an absolute necessity. The question that looms over all these discussion is the availability of a mathematical theory that allows the small scale to be ignored, which explains physical phenomena. This would imply a structure for the regularized singularity, and a recipe for successful simulation. For geometric singularities any theory is completely ad hoc and largely missing. Any such theory needs detailed and focused experimental confirmation and attention. As things work today, the basic structure is missing and is relegated to being applied in a domain science manner. We find that this is strong in fluid dynamics, and perhaps plasma physics, but almost absent in many other fields like solid mechanics, the utility of modeling and simulation suffers mightily from this.

If there is any place where singularities are dealt with systematically and properly it is fluid mechanics. Even in fluid mechanics there is a frighteningly large amount of missing territory most acutely in turbulence. The place where things really work is shock waves and we have some very bright people to thank for the order. We can calculate an immense amount of physical phenomena where shock waves are important while ignoring a tremendous amount of detail. All that matter is for the calculation to provide the appropriate integral content of dissipation from the shock wave, and the calculation is wonderfully stable and physical. It is almost never necessary and almost certainly wasteful to compute the full gory details of a shock wave.

Fluid mechanics has many nuances and details with important applications. The mathematical structure of fluids is remarkably well in hand. Boundary layer theory is another monument where our understanding is well defined. It isn’t quite as profoundly satisfying as shocks, but we can do a lot of wonderful things. Many important technological items are well defined and engineered with the able assistance of boundary layer theory. We have a great deal of faith in this knowledge and the understanding of what will happen. The state is better than it is problematic. As boundary layers get more and more exciting they lead to a place where problems abound, the problems that appear when a flow becomes turbulent. All of a sudden the structure becomes much more difficult and prediction with deep understanding starts to elude us.

The same can’t be said by and large for turbulence. We don’t understand it very well at all. We have a lot of empirical modeling and convention wisdom that allows useful science and engineering to proceed, but an understanding like we have for shock waves eludes us. It is so elusive that we have a prize (the Clay prize) focused on providing a deep understanding of the mathematical physics of its dynamics. The problem is that the physics strongly implies that the behavior of the governing equations (incompressible Navier-Stokes) admits a singularity, yet the equations don’t seem to. Such a fundamental incongruence is limiting our ability to progress. I believe the issue is the nature of the governing equations and a need to change this model away from incompressibility, which is a useful and unphysical approximation, not a fundamental physical law. In spite of all the problems, the state of affairs in turbulence is remarkably good compared with solid mechanics.

Another discontinuous behavior of great importance in practical matters are material interfaces. Again these interfaces are never truly singular in nature, but it is essential for utility to represent them that way. The capacity to use such a simple representation is challenged by a lot of things such a chemistry. More and more physics challenge the ability to use the singular representation without empirical and heavy-handed modeling. The ability to use well-defined mathematical models as opposed to ad hoc modeling implies essential understanding that belies a science that is compelling. The better the equations, the better the understanding, which is the essence of science that should provide us faith in its findings.

An example of lower mathematical maturity can be seen in the field of solid mechanics. In solids, the mathematical theory is stunted by comparison to fluids. A clear part of the issue is the approach taken by the fathers of the field in not providing a clear path for combined analytical-numerical analysis as fluids had. The result of this is a numerical background that is completely left adrift of the analytical structure of the equations. In essence the only option is to fully resolve everything in the governing equations. No structural and systematic explanation exists for the key singularities in material, which is absolutely vital for computational utility. In a nutshell the notion of the regularized singularity so powerful in fluid mechanics is foreign. This has a dramatically negative impact on the capacity of modeling and simulation to have a maximal impact.

All of these principles apply quite well to a host of other fields. In my work the areas of radiation transport and plasma physics. The merging of mathematics and physical understanding in these areas is better than solid mechanics, but not as advanced as fluid mechanics. In many respects the theories holding sway in these fields have profitably borrowed from fluid mechanics, but not to the extent necessary for a thoroughly vetted mathematical-numerical modeling framework needed for ultimate utility. Both fields suffer from immense complexity and the mathematical modeling tries to steer understanding, but ultimately various factors are holding the field back. Not the least of these is an prevailing undercurrent and intent in modeling for the World to be a well-oiled machine prone to be precisely determined.

I would posit that one of the key aspects holding fields back from progress toward a fully utilitarian capability is the death grip that Newtonian-style determinism has upon our models for the World. Its stranglehold on the philosophy of solid mechanical modeling is nearly fatal and retards progress like a proverbial anchor. To the extent that it governs our understanding in other fields (i.e., plasma physics, turbulence,…), progress is harmed. In any practical sense the World is not deterministic and modeling it as such has limited if not, negative utility. It is time to release this concept as being a useful blueprint for understanding. A far more pragmatic and useful path is to focus much greater energy on understanding the degree of unpredictability inherent in physical phenomena.

The key to making everything work is an artful combination of physical understanding with a mathematical structure. The capacity of mathematics to explain and predict nature is profound and unremittingly powerful. In the case of the singularity it is essential for useful, faithful simulations that we may put confidence in. Moreover the proper mathematical structure can alleviate the need for ad hoc mechanisms, which naturally produce less confidence and lower utility. Even where the mathematics seemingly exists like incompressible flow and turbulence, the lack of a tidy theory that fails to reproduce certain properties limits progress in profound ways. When the mathematics is even more limited and does not provide a structural explanation for what is seen like in fracture and failure in fluids, the simulations become untethered and progress is shuttered by the gaps.

I suppose my real message is that the mathematical-numerical modeling book is hardly closed and complete. It represents very real work that is needed for progress. The current approach to modeling and simulation dutifully ignores this, and produces a narrative that simply presents the value proposition that all that is needed is a faster computer. A faster computer while useful and beneficial to science is not the long pole in the tent insofar as improving the capacity of mathematical-numerical modeling to become more predictive. Indeed the long pole in the tent may well be changing the narrative about the objectives from prediction back to fundamental understanding.

The title of the post is a tongue and cheek homage to the line from the Big Lebowski, a Coen Brothers masterpiece. Like the dude in the movie, a singularity is the essence of coolness and ease of use.

If you want something new, you have to stop doing something old

― Peter F. Drucker

Low-trust environments are filled with hidden agendas, a lot of political games, interpersonal conflict, interdepartmental rivalries, and people bad-mouthing each other behind their backs while sweet-talking them to their faces. With low trust, you get a lot of rules and regulations that take the place of human judgment and creativity; you also see profound disempowerment. People will not be on the same page about what’s important.

— Stephen Covey

Being thrust into a leadership position at work has been an eye-opening experience to say the least. It makes crystal clear a whole host of issues that need to be solved. Being a problem-solver at heart, I’m searching for a root cause for all the problems that I see. One can see the symptoms all around, poor understanding, poor coordination, lack of communication, hidden agendas, ineffective vision, and intellectually vacuous goals… I’ve come more and more to the view that all of these things, evident as the day is long are simply symptomatic of a core problem. The core problem is a lack of trust so broad and deep that it rots everything it touches.

Only those who dare to fail greatly can ever achieve greatly.

― Robert F. Kennedy 

What is the basis of the lack of trust and how can it be cured or at the very least ameliorated? Are we simply fated to live in a World where the trust in our fellow man is intrinsically low?

Failure is simply the opportunity to begin again, this time more intelligently.

— Henry Ford

First, it is beneficial to understand what is at stake. With trust firmly in hand people are unleashed, and new efficiencies are possible. The trust and faith in each other causes people to work better, faster and more effectively. Second-guessing is short-circuited. The capability to achieve big things is harnessed, and lofty goals can be achieved. Communication is easy and lubricated. Without trust and faith the impacts are completely opposite and harm the capacity for excellence, progress and achievement. Whole books are written on the virtues of trust (Stephen Covey’s Speed of Trust comes to mind). Trust is a game changer, and a great enabler. It is very clear that trust is coming we are in short supply of and its harming society as a whole. Its fingerprints at work leave deep bruises and make anyone focused on progress frustrated.

Distrust is like a vicious fire that keeps going and going, even put out, it will reignite itself, devouring the good with the bad, and still feeding on empty.

― Anthony Liccione

The causes of low trust are numerous and deeply engrained in the structure of society today. For example the pervasive greed and seeming profit motive in almost all things undermines any view that people are generous. A general opening ante in any interaction is the feeling that someone is trying to gain advantage by whatever means necessary. The Internet has undermined authority-making information (and disinformation) so ubiquitous that we’ve lost the ability to sift fact from fiction. Almost every institution in society is under attack from legitimacy. All interests are viewed with suspicion and corruption seemingly abounds. We’ve never had a greater capacity to communicate with one another, yet we understand less than ever.

I’ll touch more on the greed and corruption because I think they are real and corrosive in the extreme. The issue that the basic assumption of greed and corruption is wider than its actuality and causes a lot of needless oversight and bureaucracy that lays waste to efficiency. Of course greed is a very real thing and manifests itself in our corporate culture and even celebrated by the very people who are hurt the most. The rise of Donald Trump as a viable Politician is amble evidence of just how incredibly screwed up everything has gotten. How a mildly wealthy, greedy, reality show character could ever be considered as a viable President is the clearest sign of a very sick culture. It is masking a very real problem of a society that celebrates the rich while those rich systematically prey on the whole of society leeches. They claim to be helping society even while they damage our future to feed their hunger. The deeper physic wound is the feeling that everyone is so motivated leading to the broad-based lack of trust of your fellow man.

So where do I see this in work? The first thing is the incredibly short leash we are kept on and the pervasive micromanagement. We here words like “accountability” and “management assurance”, but its really “we don’t trust you at all”. Every single activity is burdened by oversight that acts to question and second-guess every decision and even the motivations behind them. Rather than everyone knowing what the larger aims, objective and goals and assuming that there is a broad based approach to solution, people assume that folks are out to waste and defraud. We impose huge costs in time; money and effort to assure that we don’t waste a dime or hour doing anything except what you are assigned to do. All of this oversight comes at a huge cost, and the expense of the oversight is actually the tip of the proverbial iceberg. The micromanagement is so deep that it kneecaps any and all ability to be agile and adaptive in how work is done. Plans have to be followed to a tee even when it is evident that the plans didn’t really match the reality that develops upon meeting the problem.

Suspicion ruins the atmosphere of trust in a team and makes it ineffective

― Sunday Adelaja

The micromanagement has even deeper impacts on the ability to combine, collaborate and envision broader perspectives. People’s work is closely scrutinized, planned and defined. Rather than engage in deep, broad perspectives in the nature of the work, people are encouraged if not implored to focus on the specific assignments to the exclusion of all else. I’ve seen such narrowness producing deeply pathological effects such as people seeing different projects they personally work on as being executed by a different people and incapable of expressing or articulating connections between the projects even when they are obvious. These impacts are crushing the level of quality in both the direct execution of the work and the development of people in the sense of having a deep, sustained career that builds toward personal growth.

In the overall execution of work another aspect of the current environment can be characterized as the proprietary attitude. Information hiding and lack of communication seem to be a growing problem even as the capacity for transmitting information grows. Various legal, or political concerns seem to outweigh the needs for efficiency, progress and transparency. Today people seem to know much less than they used to instead of more. People are narrower and more tactical in their work rather than broader and strategic. We are encouraged to simply mind our own business rather than seek a broader attitude. The thing that really suffers in all of this is the opportunity to make progress for a better future.

Don’t be afraid to fail. Don’t waste energy trying to cover up failure. Learn from your failures and go on to the next challenge. It’s ok to fail. If you’re not failing, you’re not growing.

— H. Stanley Judd

Milestones and reporting is an epitome of bad management and revolves completely around a lack of trust. Instead of being a tool for managing effort and lubricating the communication these tools are used to dumb down work, and assure low quality, low impact work as the standard of delivery. The reporting has to have marketing value instead of information and truth-value. It is used to sell the program and assure the image of achievement rather than provide an accurate picture of the status. Problems, challenges and issues tend to be soft-pedaled and deep sixed rather than discussed openly and deeply. Project planning in milestone are anchors against progress instead of aspirational goals. There is significant structure in the attitude toward goals that drives quality and progress away from objectives. This drive is the inability to accept failure as a necessary and positive aspect of the conduct of any work that is aggressive and progressive. Instead we are encouraged to always succeed and this encouragement means goals are defined to low and trivially achievable.

I’ve written before about preponderance of bullshit as a means of communicating work. Instead of honest and clear communication of information, we see communication of things that are constructed with the purpose of deceiving rewarded. Part of the issue is the inability for the system to accept failure, accept unexpected results as contributing to bullshit. Another matter that contributes to the amount of bullshit is the lack of expertise in the value system. True experts are not trusted, or simply viewed as having a hidden agenda. Notions of nuance that color almost anything an expert might tell you are simply not trusted. Instead we favor a simple and well-crafted narrative over the truth. It is much easier to craft fiction into a compelling message than a nuanced truth. Once this path is taken it is a quick trip to complete bullshit.

How do we fix any of this?

The simplest thing to do is value the truth, value excellence and cease rewarding the sort of trust-busting actions enumerated above. Instead of allowing slip-shod work to be reported as excellence we need to make strong value judgments about the quality of work, reward excellence, and punish incompetence. The truth and fact needs to be valued above lies and spin. Bad information needs to be identified as such and eradicated without mercy. Many greedy self-interested parties are strongly inclined to seed doubt and push lies and spin. The battle is for the nature of society. Do we want to live in a World of distrust and cynicism or one of truth and faith in one another? The balance today is firmly stuck at distrust and cynicism. The issue of excellence is rather pregnant. Today everyone is an expert, and no one is an expert with the general notion of expertise being highly suspected. The impact of such a milieu is absolutely damaging to the structure of society and the prospects for progress. We need to seed, reward and nurture excellence across society instead of doubting and demonizing it.

Of course deep within this value system is the concept of failure. Failure achieved while trying to do excellent good things must cease to be punished. Today failure is equivocated with fraud and is punished even when the objectives were good and laudable. This breeds all the bad things that are corroding society. Failure is absolutely essential for learning and the development of expertise. To be an expert is to have failed, and failed in the right way. If we want to progress societally, one needs to allow, even encourage failure. We have to stop the attempts to create a fail-safe system because fail-safe quickly becomes do nothing.

What do you do with a mistake: recognize it, admit it, learn from it, forget it.

— Dean Smith

Ultimately we need to conscientiously drive for trust as a virtue in how we approach each other. A big part of trust is the need for truth in our communication. The sort of lying, spinning and bullshit in communication does nothing but undermine trust, and empower low quality work. We need to empower excellence through our actions rather than simply declare things to be excellent by definition and fiat. Failure is a necessary element in achievement and expertise. It must be encouraged. We should promote progress and quality as a necessary outcome across the broadest spectrum of work. Everything discussed above needs to be based in a definitive reality and have actual basis in facts instead of simply bullshitting about it, or it only having “truthiness”. Not being able to see the evidence of reality in claims of excellence and quality simply amplifies the problems with trust, and risks devolving into a viscous cycle dragging us down instead of a virtuous cycle that lifts us up.

If you are afraid of failure you don’t deserve to be successful!

— Charles Barkley

There is only one thing that makes a dream impossible to achieve: the fear of failure.

― Paulo Coelho

The conventional view serves to protect us from the painful job of thinking.

― John Kenneth Galbraith

I chose the name the “Regularized Singularity” because it’s so important to the conduct of computational simulations of significance. For real world computations, the nonlinearity of the models dictates that the formation of a singularity is almost a foregone conclusion. To remain well behaved and physical, the singularity must be regularized, which means the singular behavior is moderated into something computable. This almost always accomplished with the application of a dissipative mechanism and effectively imposes the second law of thermodynamics on the solution.

A useful, if not vital, tool is something called “hyperviscosity”. Taken broadly hyperviscosity is a broad spectrum of mathematical forms arising in numerical calculations. I’ll elaborate a number of the useful forms and options. Basically a hyperviscosity is viscous operator that has a higher differential order than regular viscosity. As most people know, but I’ll remind them the regular viscosity is a second-order differential operator, and it is directly proportional to a physical value of viscosity. Such viscosities are usually a weakly nonlinear function of the solution, and functions of the intensive variables (like temperature, pressure) rather than the structure of the solution. The hyperviscosity falls into a couple of broad categories, the linear form and the nonlinear form.

Unlike most people I view numerical dissipation as a good thing and an absolute necessity. This doesn’t mean that it should be wielded cavalierly or brutally because it can and gives computations a bad name. Generally conventional wisdom dictates that dissipation should always be minimized, but this is wrong-headed. One of the key aspects of important physical systems is the finite amount of dissipation produced dynamically. The correct asymptotically correct solution with a small viscosity is not zero dissipation; it is a non-zero amount of dissipation arising from the proper large-scale dynamics. This knowledge is useful in guiding the construction of good numerical viscosities that enable us to efficiently compute solutions to important physical systems.

One of the really big ideas to grapple with is the utter futility of using computers to simply crush problems into submission. For most problems of any practical significance this will not be happening, ever. In terms of the physics of the problems, this is often the coward’s way out of the issue. In my view, if nature were going to be submitting to our mastery via computational power, it would have already happened. The next generation of computing won’t be doing the trick either. Progress depends on actually thinking about modeling. A more likely outcome will be the diversion of resources away from the sort of thinking that will allow progress to be made. Most systems do not depend on the intricate details of the problem anyway. The small-scale dynamics are universal and driven by large scales. The trick to modeling these systems is to unveil the essence and core of the large-scale dynamics leading to what we observe.

Given that we aren’t going to be crushing our problems out of existence with raw computing power, hyperviscosity ends up being a handy tool to get more out of the computing we have. Viscosity depends upon having enough computational resolution to effectively allow it to dissipate energy from the computed system. If the computational mesh isn’t fine enough, the viscosity can’t stably remove the energy and the calculation blows up. This provides a very stringent limit on the resolution that can be computationally achieved.

The first form of viscosity to consider is the standard linear form in its simplest form which is a second order differential operator, . If we apply a Fourier transform to the operator we can see how simple viscosity works, (just substitute the Fourier description for the function into the operator). The viscosity grows in magnitude with the square of the wave number . Only when the product of the viscosity and wavenumber squared becomes large will the operator remove energy from the system effectively.

Linear dissipative operators only come from even orders of the differential. Moving to a fourth-order bi-Laplacian operator it is easy to see how the hyperviscosity will works, . The dissipation now kicks in faster () with the wavenumber allowing the simulation to be stabilized at comparatively coarser resolution than the corresponding simulation only stabilized by a second-order viscous operator. As a result the simulation can attack more dynamic and energetic flows with the hyperviscosity. One detail is that the sign of the operator changes with each step up the ladder, a sixth order operator will have a negative sign, and attack the spectrum of the solution even faster, , and so on.

Taking the linear approach to hyperviscosity is simple, but has a number of drawbacks from a practical point-of-view. First the linear hyperviscosity operator becomes quite broad in its extent as the order of the method increases. The method is also still predicated on a relatively well-resolved numerical solution and does not react well to discontinuous solutions. As such the linear hyperviscosity is not entirely robust for general flows. It is better as an additional dissipation mechanism with more industrial strength methods and for studies of a distinctly research flavor. Fortunately there is a class of methods that remove most of these difficulties, nonlinear hyperviscosity. Nonlinear is almost always better, or so it seems, not easier, but better.

Linearity breeds contempt

– Peter Lax

The first nonlinear viscosity came about from Prantl’s mixing length theory and still forms the foundation of most practical turbulence modeling today. For numerical work the original shock viscosity derived by Richtmyer is the simplest hyperviscosity possible, . Here is a relevant length scale for the viscosity. In purely numerical work, . It provides what linear hyperviscosity cannot, stability and robustness, making flows that would be computed with pervasive instability and making them stable and practically useful. It provides the fundamental foundation for shock capturing and the ability to compute discontinuous flows on grids. In many respects the entire CFD field is grounded upon this method. The notable aspect of the method is the dependence of the dissipation on the product of the coefficient and the absolute value of the gradient of the solution.

Looking at the functional form of the artificial viscosity, one sees that it is very much like the Prantl mixing length model of turbulence. The simplest model used for large eddy simulation (LES) is the Smagorinsky model developed first by Joseph Smagorinsky and used in the first three dimensional model for global circulation. This model is significant as the first LES and the model that is a precursor of the modern codes used to predict climate change. The LES subgrid model is really nothing more than Richtmyer (and Von Neumann’s) artificial viscosity and is used to stabilize the calculation against instability that invariably creeps in with enough simulation time. The suggestion to do this was made by Jules Charney upon seeing early weather simulations. The significance of having the first useful numerical method for capturing shock waves, and computing turbulence being one and the same is rarely commented upon. I believe this connection is important and profound. Equally valid arguments can be made that state that the form of nonlinear dissipation is fated by the dimensional form of the governing equations and the resulting dimensional analysis.

Before I derive a general form for the nonlinear hyperviscosity, I should discuss a little bit about another shortcoming of the linear hyperviscosity. In its simplest form the linear operator for classical linear viscosity produces a positive-definite operator. Its application as a numerical solution will keep positive quantities positive. This is actually a form of strong nonlinear stability. The solutions will satisfy discrete forms for the second law of thermodynamics, and provide so-called “entropy solutions”. In other words the solutions are guaranteed to be physically relevant.

This isn’t generally considered important for viscosity, but in the content of more complex systems of equations may have importance. One of the keys to bringing this up is that generally speaking linear hyperviscosity will not have this property, but we can build nonlinear hyperviscosity that will preserve this property. At some level this probably explains the utility of nonlinear hyperviscosity for shock capturing. In nonlinear hyperviscosity we have immense freedom in designing the viscosity as long as we keep it positive. We then have a positive viscosity multiplying a positive definite operator, and this provides a deep form of stability we want along with a connection that guarantees of physically relevant solutions.

With the basic principles in hand we can go wild and derive forms for the hyperviscosity that are well-suited to whatever we are doing. If we have a method with high-order accuracy, we can derive a hyperviscosity to stabilize the method that will not intrude on the accuracy of the method. For example, let’s just say we have a fourth-order accurate method, so we want a viscosity with at least a fifth order operator, . If one wanted better high-frequency damping a different form would work like . To finish the generalization of the idea consider that you have eighth-order method, now a ninth- or tenth-order viscosity would work, for example, . The point is that one can exercise immense flexibility in deriving a useful method.

I’ll finish with making brief observation about how to apply these ideas to systems of conservations laws, . This system of equations will have characteristic speeds, determined by the eigen-analysis of the flux Jacobian, . A reasonable way to think about hyperviscosity would be to write the nonlinear version as , where is the number of derivatives to take. A second approach that would work with Godunov-type methods would compute the absolute value jump at cell interfaces in the characteristic speeds where the Riemann problem is solved to set the magnitude of the viscous coefficient. This jump is the order of the approximation, and would multiply the cell-centered jump in the variables, . This would guarantee proper entropy production through the hyperviscous flux that would augment the flux computed via the Riemann solver. The hyperviscosity would not impact the formal accuracy of the method.

We can not solve our problems with the same level of thinking that created them

― Albert Einstein

I spent the last two posts railing against the way science works today and its rather dismal reflection in my professional life. I’m taking a week off. It wasn’t that last week was any better, it was actually worse. The rot in the world of science is deep, but the rot is simply part of larger World to which science is a part. Events last week were even more appalling and pregnant with concerns. Maybe if I can turn away and focus on something positive, it might be better, or simply more tolerable. Soon I have a trip to Washington and into the proverbial belly of the beast, it should be entertaining at the very least.

Till next Friday, keep all your singularities regularized.

Think before you speak. Read before you think.

― Fran Lebowitz

VonNeumann, John, and Robert D. Richtmyer. “A method for the numerical calculation of hydrodynamic shocks.” Journal of applied physics 21.3 (1950): 232-237.

Borue, Vadim, and Steven A. Orszag. “Local energy flux and subgrid-scale statistics in three-dimensional turbulence.” Journal of Fluid Mechanics 366 (1998): 1-31.

Cook, Andrew W., and William H. Cabot. “Hyperviscosity for shock-turbulence interactions.” Journal of Computational Physics 203.2 (2005): 379-385.

Smagorinsky, Joseph. “General circulation experiments with the primitive equations: I. the basic experiment*.” Monthly weather review 91.3 (1963): 99-164.